An elevator accelerates from rest at a constant rate $α$ for time interval $t_{1}$ and travels a distance $S_{1}$ It them retards at a constant rate $β$ for time interval $t_{2}$ and finally comes to rest after travelling a distance $S_{2}$ during its retardation Show that:
$\frac{S_{1}}{S_{2}} = \frac{t_{1}}{t_{2}} = \frac{β}{α}$ .

Video Solution

Text Solution

Verified by Experts

Velocity-time graph for the above situation is as follows:

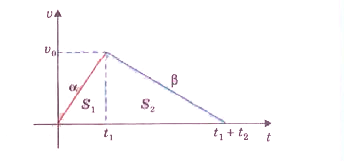
Maximum velocity attained by the elevator is $v_{0}$ . Slope of the v-t graph represents acceleration of the body, hence we can write the following relation:
$α = \frac{v_{0}}{t_{1}}$ and $β = \frac{v_{0}}{t_{2}}$
$\Rightarrow \frac{α}{β} = \frac{t_{2}}{t_{1}}$
Area under the v-t graph represents displacement, hence we can write the following,
$S_{1} = \frac{1}{2} v_{0} t_{1}$ and $S_{2} = \frac{1}{2} v_{0} t_{2}$
Dividing the above two equation e get
$\frac{S_{1}}{S_{2}} = \frac{t_{1}}{t_{2}} = \frac{β}{α}$

A train accelerates from rest at a constant rate a for distance $x_{1}$ and time $t_{91})$ . After that is retards at constant rate $β$ for distance $x_{2}$ and time $t_{2}$ and comes to the rest. Which of the following relation is correct:-
A $\frac{x_{1}}{x_{2}} = \frac{α}{β} = \frac{t_{1}}{t_{2}}$
B $\frac{x_{1}}{t_{2}} = \frac{β}{α} = \frac{t_{1}}{t_{2}}$
C $\frac{x_{1}}{x_{2}} = \frac{α}{β} = \frac{t_{2}}{t_{1}}$
D $\frac{x_{1}}{x_{2}} = \frac{β}{α} = \frac{t_{2}}{t_{1}}$
A train accelerates from rest at a constant rate for distance $\X1$ and time . $\t1$ After that retards to rst at constant rate for distance $X_{2}$ and time $t_{2}$ . Then, it is found that
A $\frac{X_{1}}{X_{2}} = \frac{α}{β} = \frac{t_{1}}{t_{2}}$
B $\frac{X_{1}}{X_{2}} = \frac{α}{β} = \frac{t_{2}}{t_{1}}$
C $\frac{X_{1}}{X_{2}} = \frac{β}{α} = \frac{t_{1}}{t_{2}}$
D $\frac{X_{1}}{X_{2}} = \frac{β}{α} = \frac{t_{2}}{t_{1}}$
A train moves from rest with acceleration $α$ and in time $t_{1}$ covers a distance x. It then decelerates rest at constant retardation $β$ for distance y in time $t_{2}$ . Then
A $\frac{x}{y} = \frac{β}{α}$
B $\frac{β}{α} = \frac{t_{1}}{t_{2}}$
Cx=y
D $\frac{x}{y} = \frac{β t_{1}}{α t_{2}}$