A particle starts moving rectilinearly at time t=0 such that its velocity v changes with time t according to the equation v=t2−t, where t is in seconds and v in ms−1. Find the time interval for which the particle retards.
Velocity v=t2−t=t(t−1)
Acceleration, a=dvDt=2t−1
Motion of particle is considered as retarding motion when v and a have opposite signs that means they are along opposite directions.
From equation 1 we can see that,
velocity is positive when t>1
velocity is negative when t<1
From equation 2 we can see that,
Acceleration is positive when t>1/2
Acceleration is negative when t<1/2
From above results we can see that when velocity is positive then acceleration cannot be negative
But there is an interval 12<t<1, when velocity is negative and acceleration is positive, hence this is the interval of time when particle retards.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - NCERT (TEXTBOOK EXERCISES )
22 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - NCERT (ADDITIONAL EXERCISE)
6 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CONCEPTUAL QUESTIONS
14 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)
12 Videos
Similar Questions
A particle starts moving rectilinearly at time t=0 such that its velocity(v) changes with time (t) as per equation –
v=(t2–2t)m/s for 0<t<2s
=(–t2+6t–8)m/s for 2≤te4s
(a) Find the interval of time between t=0 and t=4s when particle is retarding.
(b) Find the maximum speed of the particle in the interval 0≤t≤4s.
View SolutionA particle moving in a straight line has its velocit varying with time according to relation v=t2−6t+8(m/s) where t is in seconds. The CORRECT statement(s) about motion of this particle is/are:-
View Solution
Knowledge Check
A particle starts moving rectilinearly at time t = 0 such that its velocity v changes with time t according to the equation v=t2−t, where t is in seconds and v is in ms−1. The time interval for which the particle retrads (i.e., magnitude of velocity decreases)is
At<1/2B1/2<t<1Ct>1Dt<1/2andt>1A particle starts moving rectillineraly at time t=0, such that its velocity 'v' changes with time 't' according to the equation v=t2−t where t is in seconds and v is in m/s. The time interval for which the particle retards is
At<1/2B1/2<t<1Ct>1Dt<1/2 and t>1Velocity of a particle of mass 2kg varies with time t according to the equation →v=(2tˆi+4ˆj)m/s. Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.
A2ˆim/sB4ˆim/sC8ˆim/sD6ˆim/s
Velocity of particle of mass 2kg varies with time t accoridng to the equation →v=(2tˆi+4ˆj)ms−1. Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.
View SolutionA particle is moving along x-axis such that its velocity varies with time according to v=(3m/s2)t−(2m/s3)t2. Find the velocity at t = 1 s and average velocity of the particle for the interval t = 0 to t = 5 s.
View SolutionA particle moves on x-axis with a velocity which depends on time as per equation v=t2−8t+15(m/s) where time t is in seconds. Match the columns.
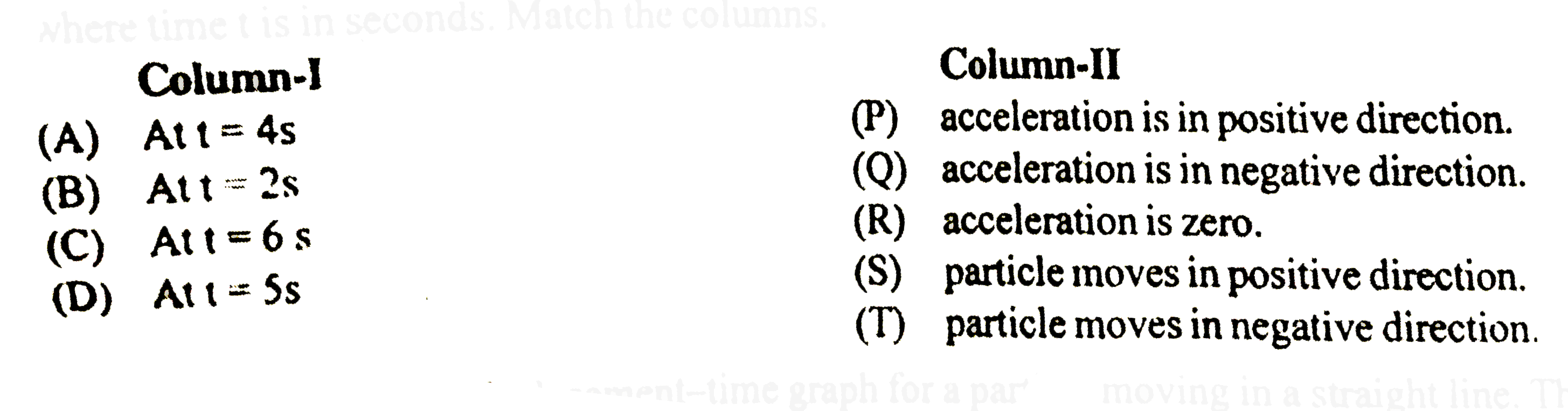
View SolutionA particle moves along x-axis in such a way that its r-coordinate varies with time't according to the equation x= (8−4t+6t2) metre. The velocity of the particle will vary with time according to the graph
View SolutionA particle moves along x-axis in such a way that its x-coordinate varies with time t according to the equation x=(8−4t+6t2) metre.
The velocity of the particle will vary with time according to the graph :-
View Solution
