An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
4. The maximum separation between the floor of elevator and the ball during its flight would be
12 m
15 m
9.5 m
7.5 m
The correct Answer is:C
At maximum separation, their velocities are same
∴25−−10t=10+5t
or t=1s
Maximum separation =2+S2−S1
=2+[25×1−5×(1)2]−[10×1+2.5(1)2]
=9.5m
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Subjective Questions24videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - SCQ_TYPE39videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - More Than One Correct6videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
1. The time in which the ball strikes the floor of elevator is given byView SolutionAn elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
2. The maximum height reached by ball, as measured from the ground would beView SolutionAn elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
3. Displacement of ball with respect to ground during its night would beView SolutionAn elevator without a ceiling is ascending with a constant speed of 10 m//s. A boy on the elevator shoots a ball directly upward, from a height of 2.0 m above the elevator floor. At this time the elevator floor is 28 m above the ground. The initial speed of the ball with respect to the elevator is 20 m//s. (Take g=9.8m/s2)
(a) What maximum height above the ground does the ball reach?
(b) How long does the ball take to return to the elevator floor?View Solution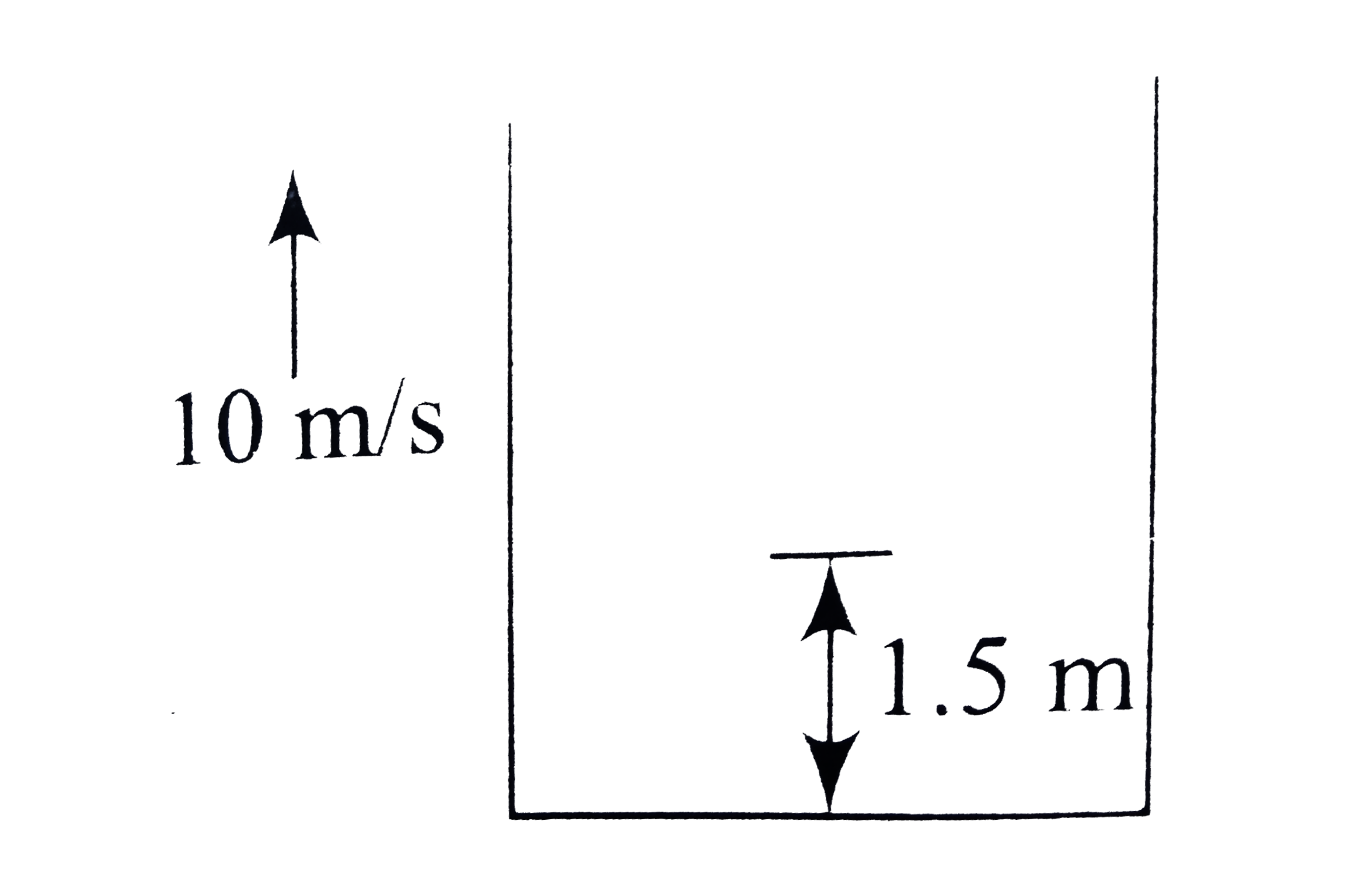
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the maximum height reached by the bullet relative to the ground :View Solution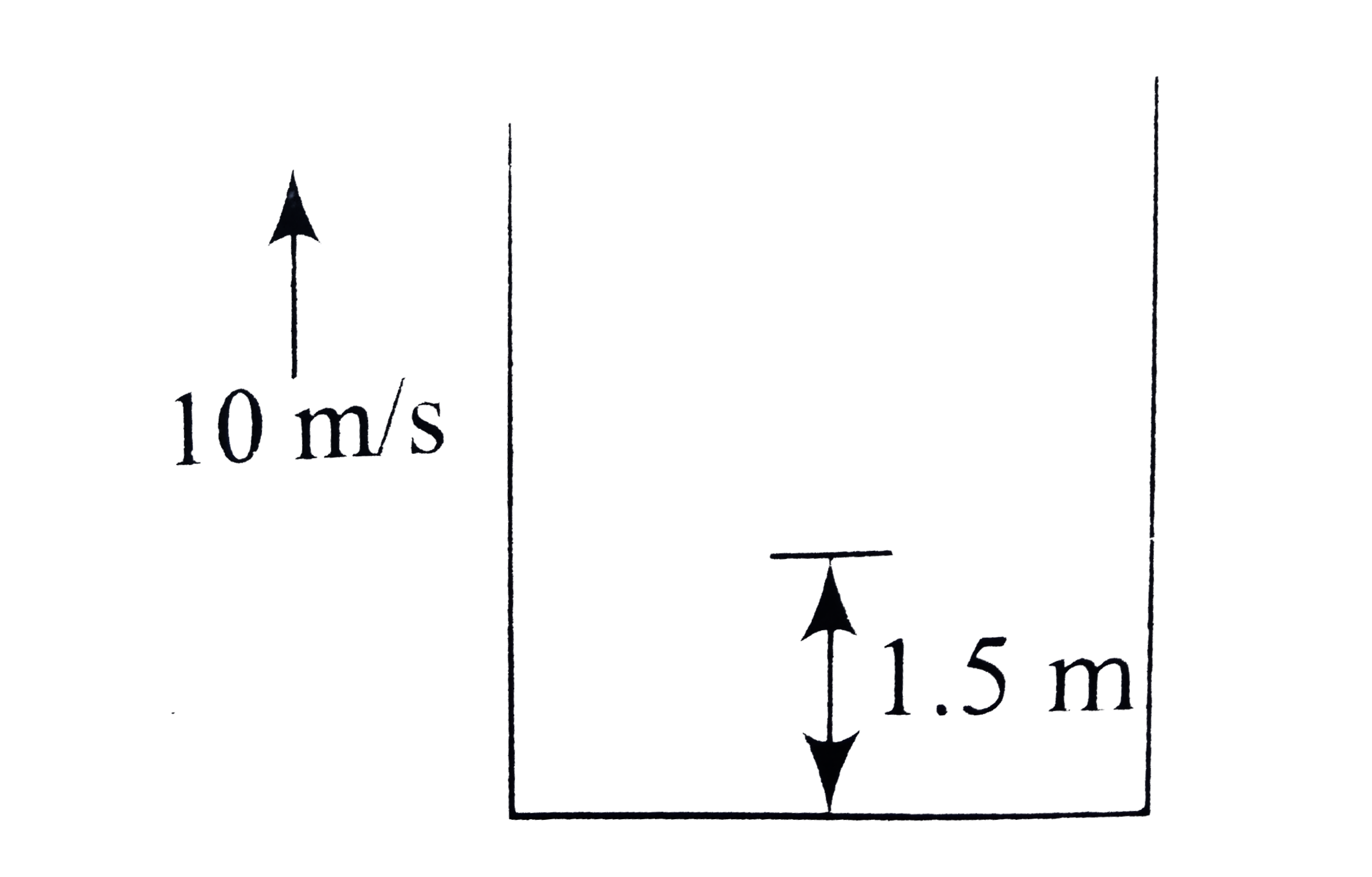
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the acceleration of the elevator in upward direction, (mss2):View Solution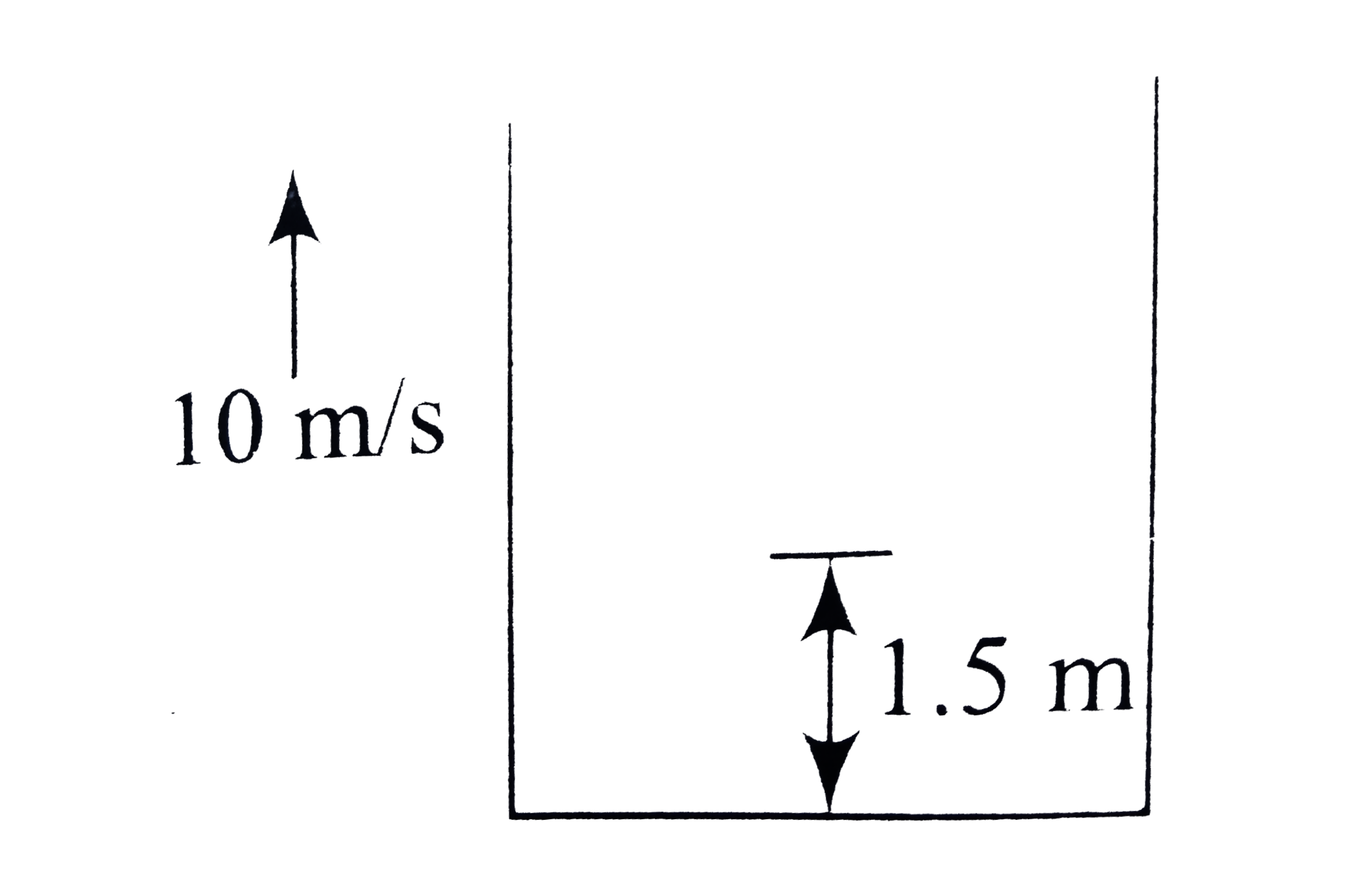
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the displacement of the bullet relative to ground during its flight:View SolutionAn elevator whose floor-to-ceiling destance is 2.50m starts ascending with a constant acceleration of 1.25ms−2 On second after the start, a bolt begins falling from the elevator. Calculate the free fall time of the bolt
View SolutionSuppose the ceiling in the previous problem is that the elevator which is going up with an acceleration of 2.0ms2. Find the elongations.
View SolutionStarting from rest, A lift moves up with an acceleration of 2ms−2. In this lift , a ball is dropped from a height of 1.5m (with respect to floor of lift). The time taken by the ball to reach the floor of the lift is (g=10ms−2)
View Solution