An equilateral glass prism (μ−1.6) is immersed in water (μ=1.33). Calculate the angle of deviation produced for a ray of light incident at 40∘ on one face of the prism.
To solve the problem step by step, we will follow the procedure outlined in the video transcript while breaking it down into clear steps.
Step 1: Calculate the Refractive Index of Glass with Respect to Water
The refractive index of the glass prism with respect to water (μg/w) can be calculated using the formula:
μg/w=μgμw=1.61.33
Calculating this gives:
μg/w≈1.203
Step 2: Calculate the Angle of Refraction (R1)
Using Snell's Law at the first interface (air to glass), we have:
sinI1sinR1=μg/w
Substituting the known values:
sin40∘sinR1=1.203
Rearranging gives:
sinR1=sin40∘1.203
Calculating this, we find:
R1≈32∘18′
Step 3: Calculate R2
For an equilateral prism, the sum of the angles of refraction at the two interfaces is equal to the angle of the prism (A). For an equilateral prism, A = 60°.
Thus, we have:
R1+R2=A⟹R2=60∘−R1
Substituting the value of R1:
R2=60∘−32∘18′≈27∘42′
Step 4: Calculate the Angle of Incidence (I2) at the Second Interface
Using Snell's Law again at the second interface (glass to water):
sinR2sinI2=μg/w
Substituting the known values:
sin27∘42′sinI2=1.203
Rearranging gives:
sinI2=μg/w⋅sinR2
Calculating this, we find:
I2≈34∘
Step 5: Calculate the Angle of Deviation (Δ)
The angle of deviation (Δ) is given by the formula:
Δ=I1+I2−A
Substituting the known values:
Δ=40∘+34∘−60∘
Calculating this gives:
Δ=14∘
Final Answer
The angle of deviation produced for a ray of light incident at 40° on one face of the prism is:
Δ=14∘
The refractive index of the glass prism with respect to water (μg/w) can be calculated using the formula:
μg/w=μgμw=1.61.33
Calculating this gives:
μg/w≈1.203
Using Snell's Law at the first interface (air to glass), we have:
sinI1sinR1=μg/w
Substituting the known values:
sin40∘sinR1=1.203
Rearranging gives:
sinR1=sin40∘1.203
Calculating this, we find:
R1≈32∘18′
For an equilateral prism, the sum of the angles of refraction at the two interfaces is equal to the angle of the prism (A). For an equilateral prism, A = 60°.
Thus, we have:
R1+R2=A⟹R2=60∘−R1
Substituting the value of R1:
R2=60∘−32∘18′≈27∘42′
Using Snell's Law again at the second interface (glass to water):
sinR2sinI2=μg/w
Substituting the known values:
sin27∘42′sinI2=1.203
Rearranging gives:
sinI2=μg/w⋅sinR2
Calculating this, we find:
I2≈34∘
The angle of deviation (Δ) is given by the formula:
Δ=I1+I2−A
Substituting the known values:
Δ=40∘+34∘−60∘
Calculating this gives:
Δ=14∘
The angle of deviation produced for a ray of light incident at 40° on one face of the prism is:
Δ=14∘
Topper's Solved these Questions
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Solved Example(d)
Explore 32 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Conceptual problem(b)
Explore 22 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Solved Example(b)
Explore 61 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
Similar Questions
An equilateral glass prism of refractive index 1.5 is immersed in water. Find the angle of deviation produced when a ray of light is incident at 42∘ on one face of the prism.
(Refractive index of water = 1.33)
View SolutionA glass prism of angle 72∘ and refractive index 1.66 is immersed in a liquid of μ=1.33. Calculate the angle of minimum deviation.
View Solution
Knowledge Check
A thin glass prism of μ=1.5 is immersed in water of μ=1.33 . The ratio of deviation of the ray in water to that in air for the same prism is
A1:4B1:2C1:8D1:3An equilateral prism produces an angle of deviation 60∘ when the angle of incidence is 60∘. The angle of deviation produced when the ray is incident normal to the surface is
A30∘B45∘C60∘Dcan't be determined
Light is incident from glass (μ=1.50) to water (μ=1.33) find the range of the angle of deviation for which there are two angles of incidence.
View Solution(i) A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 30∘. Calculate the speed of the light through the prism.
(ii) Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.
View SolutionFor a glass prism (μ=√3) the angle of minimum deviation is equal to the angle of the prism. Find the angle of the prism.
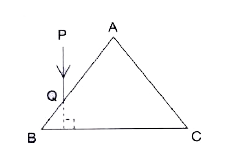
View SolutionA ray of light PQ is incident on the face AB of an equilateral glass prism ABC as shown in the figure. Show that angle of emergence = angle of deviation. Also, with a ray diagram, trace the path of the emergent ray.
View SolutionA prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. By rotating the prism, the minimum angle of deviation is measured to be 40∘. What is the refractive index of the prism ? If the prism is placed in water (μ=1.33), predict the new angle of minimum deviation of the parallel beam. The refracting angle of prism is 60∘.
View Solution(a) Deduce the expression, by drawing a suitable ray diagram, for the refractive index of a triangular glass prisms in terms of the angle of minimum deviation (D) and the angle of prism (A).
Draw a plot showing the variation of the angle of deviation with the angle of incidence.
(b) Calculate the value of the angle of incidence when a ray of light incident on one face of an equilateral glass prism produces the emergent ray, which just grazes along the adjacent face. Refractive index of prism is √2
View Solution