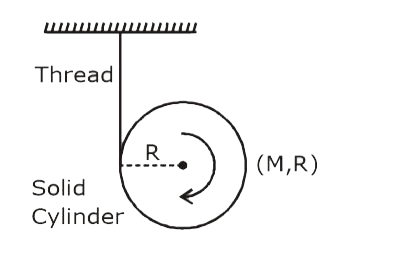
An extensible string is wound over a rough pulley of mass $M_{1}$ and radius $R$ and a cylinder of mass $M_{2}$ and radius $R$ such that as the cylinder rolls down. The string un wounds over the pulley as well the cylinder. Find the acceleration of cylinder $M_{2}$ .

Video Solution

Text Solution

Verified by Experts

Through this illustration we will learn the application of torque equation and constraint relation in more complex case here. We have change the block with cylinder $M_{2}$ Pulley $M_{1}$ will have oly pure rotation while cylinder $M_{2}$ will have rotatioin and translation combined. Let us analyse step by step in the same way as the previous illustration.
Step I: Analyse the motion of the pulley and the cyinder. Pulley: One rotational acceleration $α_{1}$ (clockwise)
Cylinder: One rotational acceleration $α_{2}$ (clockwise) andn a linear acceleration $a_{2}$ (downward)
Step II: Equation of motion for $M_{2}$
$M_{2} g - T = M_{2} a_{2}$ ..........i
Step III: Torque equation for pulley $τ_{c} = I_{c} α$
$T R = (\frac{M_{1} R^{2}}{2}) α_{1} \Rightarrow \frac{2 T}{M_{1} R}$ .......ii
Torquue equation for the cylinder (about centre of mass of cylinder $τ_{c} = I_{c} α$
$\Rightarrow T R = (\frac{M_{2} R^{2}}{2}) α_{2}$
$α_{2} = \frac{2 T}{M_{2} R}$ .........iii
Step IV: The acceleration of $P$ and $Q$ should be equal as both are connected with the same inextensible string ltbr> Accceleration of $P, a_{M} = α_{1} R$ (downward) .........iv
Acceleration of $Q, a_{N} = a_{2} - α_{2} R$ (downwards) .............. v
Hence, constraint relation $α_{1} R = a_{2} - α_{2} R$ .............vi
Step V: Solving equations
After solving eqn i, ii, iii and iv, we get
$a_{2} = [\frac{(2 M_{1} + M_{2})}{3 M_{1} + 2 M_{2}}] g$

Updated on:21/07/2023