An external device, e.g an electric motor supplies constant power to a rotating system e.g., a flywheel through a torque τ power angular velocity of the system is ω Both τ and ω are variable
ω∝τ
ω∝1τ
ω∝√τ
ω∝1√τ
The correct Answer is:b
Step by step video, text & image solution for An external device, e.g an electric motor supplies constant power to a rotating system e.g., a flywheel through a torque tau power angular velocity of the system is omega Both tau and omega are variable by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The device shown in Fig. rotates on the vertical axle as shown. The frame has negligible mass as compared to the four masses each of mass m. Initial angular velocity of the system is ω0. Due to an internal mechanism the spokes in the frame lengthen so that the radii of the masses become 2a. Initially, it was a. What will be the new angular velocity of the system?
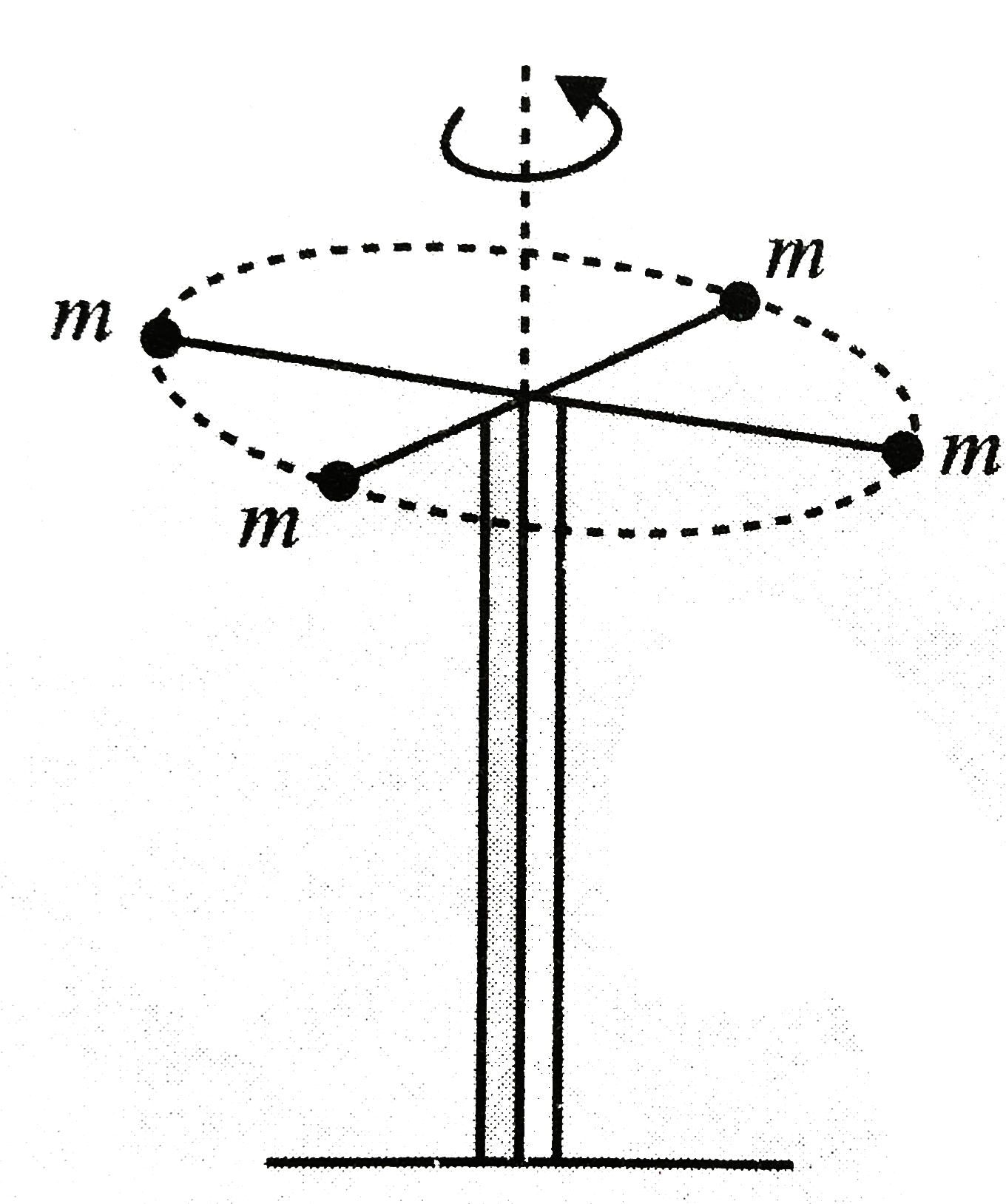
View SolutionA solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View Solution
Knowledge Check
A constant power is suppied to a rotating disc. The relationship between the angular velocity (ω) of the disc and number of rotations (n) made by the disc is governed by
Aω∝n13Bω∝n23Cω∝n32Dω∝n2An electric motor rotates a wheel at a constant angular velocity (ω) while opposing torque is τ. The power of that electric motor is
Aτω2BτωC2τωDτωAn electric motor exerts a constant torque 5Nm on a fly wheel by which it is rotated at the rate of 420r± The power of motor is
A110waB150waC220waD300wa
Calculate the instantaneous power of a body rotating with angular velocity of 20rad/s−2, when an external torque of 5Nm is applied to it.
Hint : P=τω.
View SolutionAn electric motor rotates a wheel at a constant angular velocity 10rps while opposing torque is 10Nm. The power of that electric motor is
View SolutionA constant external torque τ acts for a very brief period Δt on a rotating system having moment of inertia I.
(i) The angular momentum of the system will change by τΔt
(ii) The angular velocity of the system will change by (τΔt)/I.
(iii) If the system was initially at rest, it will acquire rotational kinetic energy (τΔt)2/2I.
(iv) The kinetic energy of the system will change by (τΔt)2I.
View SolutionA constant external torque τ acts for a very brief period △t on a rotating system having moment of inertia I then
View SolutionIf I, α and τ are the moment of inertia, angular acceleration and torque respectively of a body rotating about an axis with angular velocity ω then,
View Solution
