A constant external torque τ acts for a very brief period Δt on a rotating system having moment of inertia I.
(i) The angular momentum of the system will change by τΔt
(ii) The angular velocity of the system will change by (τΔt)/I.
(iii) If the system was initially at rest, it will acquire rotational kinetic energy (τΔt)2/2I.
(iv) The kinetic energy of the system will change by (τΔt)2I.
(i),(ii)
(i),(ii),(iii)
(ii),(iv)
(i),(iii),(iv)
ΔL=τΔt
IΔω=τΔt⇒Δω=τΔtI
Δω=ω−0=τΔtI
KR=12Iω2=12I(τΔtI)2=(τΔt)22I
Topper's Solved these Questions
Similar Questions
Prove that the rate of change of total angular momentum of a system of particles is equal to the total torque acting on the system.
View SolutionIf angular momentum is conserved in a system whose moment of inertia is decreased, will its rotational kinetic energy be also conserved ? Explain.
View Solution
Knowledge Check
- Question 1 - Select One or More
A constant external torque τ acts for a very brief period △t on a rotating system having moment of inertia I then
Athe angular velocity of the system will change by τ△t/IBthe angular velocity of the system will change by τ△t/ICif the system was initially at rest, it will acquire rotational kinetic enegy (τ△t)2/2IDthe kinetic energy of the system will change by (τ△t)2/(2I) - Question 2 - Select One
The rotational kinetic energy of a body is E and its moment of inertia is I. The angular momentum is
AEIB2√(EI)C√(2EI)DEI - Question 3 - Select One
If I, α and τ are the moment of inertia, angular acceleration and torque respectively of a body rotating about an axis with angular velocity ω then,
Aτ=IαBτ=I.ωCτ=I/ωDα=τ.ω
Find the equillibrium length for the system after increasing temperature by ΔT.
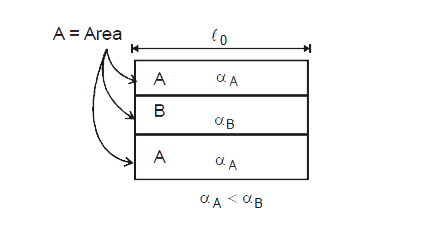 View Solution
View SolutionIf L is the angular momentum and I is the moment of inertia of a rotating body, then L22I represents its
View SolutionIf angular momentum is conserved in a system whose moment of inertia is decreased, will rotational kinetic energy be conserved.
View SolutionLet ΔU1andΔU2 be the changes in energy of the system in the process A and B then.
 View Solution
View SolutionThe relation between the torque τ and angular momentum L of a body of moment of inertia I rotating with angular velocity ω is
View Solution

