An ice cube floats in water. What percentage of volume is outside water. Density of water =1g/cc, density of ice =0.9g/cc.
To solve the problem of determining what percentage of the volume of an ice cube is outside of the water when it is floating, we can follow these steps:
1. Understand the Given Densities:
- Density of water (ρwater) = 1 g/cm³
- Density of ice (ρice) = 0.9 g/cm³
2. Apply the Principle of Buoyancy:
- When an object floats, the weight of the water displaced by the object is equal to the weight of the object itself.
- Let V be the total volume of the ice cube.
- The volume of the ice cube submerged in water can be denoted as Vsubmerged.
- The weight of the ice cube can be expressed as:
Wice=ρice⋅V⋅g
- The weight of the water displaced by the submerged part of the ice cube is:
Wdisplaced=ρwater⋅Vsubmerged⋅g
3. Set Up the Equation:
- According to the principle of buoyancy:
Wice=Wdisplaced
- Substituting the expressions for weight:
ρice⋅V⋅g=ρwater⋅Vsubmerged⋅g
- We can cancel g from both sides:
ρice⋅V=ρwater⋅Vsubmerged
4. Relate the Volumes:
- Rearranging gives us:
Vsubmerged=ρiceρwater⋅V
- Substituting the given densities:
Vsubmerged=0.91⋅V=0.9V
5. Calculate the Volume Outside Water:
- The volume of the ice cube that is outside the water is:
Voutside=V−Vsubmerged=V−0.9V=0.1V
6. Find the Percentage of Volume Outside Water:
- To find the percentage of the volume that is outside the water:
Percentage outside=(VoutsideV)×100=(0.1VV)×100=10%
Final Answer:
The percentage of the volume of the ice cube that is outside the water is 10%.
- Density of water (ρwater) = 1 g/cm³
- Density of ice (ρice) = 0.9 g/cm³
- When an object floats, the weight of the water displaced by the object is equal to the weight of the object itself.
- Let V be the total volume of the ice cube.
- The volume of the ice cube submerged in water can be denoted as Vsubmerged.
- The weight of the ice cube can be expressed as:
Wice=ρice⋅V⋅g
- The weight of the water displaced by the submerged part of the ice cube is:
Wdisplaced=ρwater⋅Vsubmerged⋅g
- According to the principle of buoyancy:
Wice=Wdisplaced
- Substituting the expressions for weight:
ρice⋅V⋅g=ρwater⋅Vsubmerged⋅g
- We can cancel g from both sides:
ρice⋅V=ρwater⋅Vsubmerged
- Rearranging gives us:
Vsubmerged=ρiceρwater⋅V
- Substituting the given densities:
Vsubmerged=0.91⋅V=0.9V
- The volume of the ice cube that is outside the water is:
Voutside=V−Vsubmerged=V−0.9V=0.1V
- To find the percentage of the volume that is outside the water:
Percentage outside=(VoutsideV)×100=(0.1VV)×100=10%
The percentage of the volume of the ice cube that is outside the water is 10%.
Topper's Solved these Questions
Similar Questions
A pieceo of ice is floating in water . Find the fraction of volume of he piece of ice outside the water
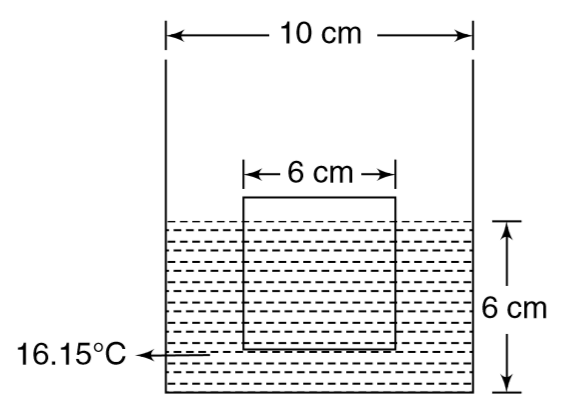
(Given density of ice =900kg/m3 and density of water =1000kg/m3)View SolutionA container has a square cross-section of 10cm×10cm. A cubical ice block of side length 6 cm is floating in water in the container. Water level in the container is 6 cm high. The ice block is at a temperature of 0∘C and the water is at 16.15∘C. Assume that heat exchange take place between the ice block and water only. What length of ice block will remain submerged in water when the system reaches thermal equilibrium? Assume that the ice block maintains its cubical shape as it melts. Take - density of ice =0.9g/cc, density of water = 1.0g/cc
Specific heat capacity of water =1calg−1.∘C−1, Specific latent heat of fusion of ice =80calg−1
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Assertion : Ice cube floats on water.
Reason : Density of ice is less than that of water.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false. - Question 2 - Select One
Iceberg floats in sea water with a part of it submerged. The percentage fraction of the ice berg submerged is (density of ice = 0.9gcm−3, density of sea water = 1.1gcm−3)
A18%B12%C10%D8% - Question 3 - Select One
An iceberg is floating partly immersed in sea water, the density of sea water is 1.03gcm−3 and that of ice is 0.92gcm−3. The fraction of the total volume of the iceberg above the level of sea water is
A8.1%B11%C34%D0.8%
An iceberg is floating partly immersed in sea water, the density of sea water is 1.03 g and that of ice is 0.92 g . The fraction of the total volume of the iceberg above the level of sea water is
View SolutionDensity of water is less than 1g/c.c ______
View SolutionDensity of water is less than 1g/c.c ______
View SolutionIce berg floats in water with part of it submerged. What is the fraction of the volume of iceberg suberged, if the density of ice is ρl=0.917g/cm3?
View SolutionA cube of density 250 kg/m2 floats in water, then what part of total volume of the cube outside the water?
View Solution

