The height to which a cylindrical vessel be filled with a homogenous liquid, to make the average force with which the liquid presses the side of the vessel equal to the force exerted by the liquid on the bottom of the vessel, is equal to.
half of the radius of the vessel
radius of the vessel
one-fourth of the radius of the vessel
three-fourth of the radius of the vessel.
The correct Answer is:B
To solve the problem, we need to find the height h of a homogeneous liquid in a cylindrical vessel such that the average force exerted by the liquid on the sides of the vessel equals the force exerted by the liquid on the bottom of the vessel.
1. Understanding the Forces:
- The force exerted by the liquid on the bottom of the vessel can be calculated using the formula:
Fbottom=Pbottom×A
where Pbottom=ρgh (pressure at the bottom), ρ is the density of the liquid, g is the acceleration due to gravity, and A is the area of the base of the cylinder.
2. Calculating the Force on the Bottom:
- Therefore, we have:
Fbottom=(ρgh)×A
3. Calculating the Average Force on the Sides:
- The pressure at any height y in the liquid is given by P(y)=ρgy.
- The average pressure on the side of the vessel from height 0 to height h is:
Pavg=Pmin+Pmax2=0+ρgh2=ρgh2
- The force exerted by this average pressure on the side of the vessel is:
Fsides=Pavg×Area of the side
- The area of the side of the cylinder is 2πrh, where r is the radius of the cylinder.
4. Calculating the Force on the Sides:
- Thus, we have:
Fsides=(ρgh2)×(2πrh)=ρghπrh
5. Setting the Forces Equal:
- To find the height h where the average force on the sides equals the force on the bottom, we set:
Fbottom=Fsides
- This gives us:
(ρgh)A=ρghπrh
6. Simplifying the Equation:
- Since A=πr2 (the area of the base), we substitute:
(ρgh)(πr2)=ρghπrh
- Dividing both sides by ρgh (assuming h≠0):
πr2=πrh
7. Solving for Height:
- Dividing both sides by πr (assuming r≠0):
r=h
- Therefore, the height h to which the cylindrical vessel should be filled is equal to the radius r of the cylinder.
Final Answer:
h=r
- The force exerted by the liquid on the bottom of the vessel can be calculated using the formula:
Fbottom=Pbottom×A
where Pbottom=ρgh (pressure at the bottom), ρ is the density of the liquid, g is the acceleration due to gravity, and A is the area of the base of the cylinder.
- Therefore, we have:
Fbottom=(ρgh)×A
- The pressure at any height y in the liquid is given by P(y)=ρgy.
- The average pressure on the side of the vessel from height 0 to height h is:
Pavg=Pmin+Pmax2=0+ρgh2=ρgh2
- The force exerted by this average pressure on the side of the vessel is:
Fsides=Pavg×Area of the side
- The area of the side of the cylinder is 2πrh, where r is the radius of the cylinder.
- Thus, we have:
Fsides=(ρgh2)×(2πrh)=ρghπrh
- To find the height h where the average force on the sides equals the force on the bottom, we set:
Fbottom=Fsides
- This gives us:
(ρgh)A=ρghπrh
- Since A=πr2 (the area of the base), we substitute:
(ρgh)(πr2)=ρghπrh
- Dividing both sides by ρgh (assuming h≠0):
πr2=πrh
- Dividing both sides by πr (assuming r≠0):
r=h
- Therefore, the height h to which the cylindrical vessel should be filled is equal to the radius r of the cylinder.
h=r
Topper's Solved these Questions
Similar Questions
To what height should a cyclindrical vessel be filled with a homogeneous liquid to make the force with which the liquid pressure on the sides of the vessel equal to the force exerted by the liquid on the bottom of the vessel ?
View SolutionTo what height should a cylindrical vessel be filled with a homogenous liquid to make to force on bottom equal to force on side? (R = radius of vessel )
View Solution
Knowledge Check
- Question 1 - Select One
To what height should a cyclindrical vessel be filled with a homogeneous liquid to make the force with which the liquid pressure on the sides of the vessel equal to the force exerted by the liquid on the bottom of the vessel ?
Aequal to the radiusBless than radiusCmore than radiusDfour times of radius - Question 2 - Select One
A cylindrical vessel of radius r is filled with a homogeneous liquid upto a height h. It is found that the force exerted by the liquid column on the bottom of the cylinder is equal to the force exerted by the liquid on the sides of the cylinder. What is the relation between r and h?
Ar=h2Br=hCr=2hDr=32h - Question 3 - Select One
To what height h should a cylindrical vessel of diameter d be filled with a liquid so that the total force on the vertical surface of the vessel be equal to the force on the bottom-
Ah=dBh=2dCh=3dDh=d/2
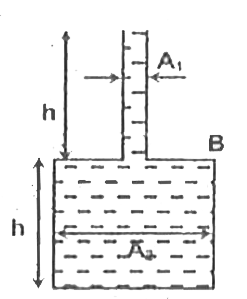
The vessel shown in the figure has two sections of area of cross - section A1andA2 .A liquid of density ρ fills both the section upto a height h in each . Consider atmospheric pressure P0 also . Find
(a) the pressure at the base of vessel .
(b) the force exerted by the liquid on the base of the vessel .
(c ) the downward force exerted by the walls of the vessel at the level B
 View Solution
View SolutionA person looking through a telescope focuses the lens at a point on the edge of the bottom of an empty cylindrical vessel Next he fills the entire vessel with a liquid of refractive index μ, without disturbing the telescope. Now, he observes the midpoint of the bottom of the vessel Determine the radius to depth ratio of the vessel
View SolutionA liquid kept in a cylindrical vessel of radius 0.3 m is rotated with a speed 2 r.p.s. The difference in the height of the liquid at the centre of the vessel and at it's sides it
View SolutionIn the following figure shown, a liquid is filled into the vessel up to a height h and the forces exerted against the liquid by the walls of the vessel are shown by arrows, the force being everywhere perpendicular to the walls of the vessel. For this situation mark out the correct statement(s).
 View Solution
View SolutionA vessel in the shape of a hollow hemisphere surmounted by a once is held with the axis vertical and vertex uppermost. If it be filled with a liquid so as to submerge half the axis of the cone in the liquid, and the height of the cone be double the radius of its base, find the liquid on the vessel is x times the weight of the liquid that the hemisphere can hold.
View Solution

