An ideal fluid flows through a pipe of circular cross section made of two section with diamters 2.5 cm and 9.76 cm. The ratio of the velocities in the two pipes is
9:4
3:2
√3:√2
√2:√3
The correct Answer is:A
To solve the problem of finding the ratio of velocities in two sections of a pipe with different diameters, we can use the principle of conservation of mass for incompressible fluids, which states that the product of the cross-sectional area and the velocity of flow must remain constant throughout the pipe. This is known as the equation of continuity.
1. Identify the Given Data:
- Diameter of the first section (D1) = 2.5 cm
- Diameter of the second section (D2) = 9.76 cm
2. Calculate the Cross-Sectional Areas:
- The cross-sectional area (A) of a circular pipe is given by the formula:
A=π(D2)2
- For the first section (A1):
A1=π(D12)2=π(2.52)2=π(1.25)2=π×1.5625
- For the second section (A2):
A2=π(D22)2=π(9.762)2=π(4.88)2=π×23.8144
3. Apply the Equation of Continuity:
- According to the equation of continuity:
A1⋅V1=A2⋅V2
- Rearranging gives us:
V1V2=A2A1
4. Substituting the Areas:
- Substitute the areas calculated:
V1V2=A2A1=π×23.8144π×1.5625
- The π cancels out:
V1V2=23.81441.5625
5. Calculate the Ratio:
- Performing the division:
V1V2=15.21
6. Conclusion:
- Therefore, the ratio of the velocities V1 to V2 is:
V1:V2=15.21:1
- Diameter of the first section (D1) = 2.5 cm
- Diameter of the second section (D2) = 9.76 cm
- The cross-sectional area (A) of a circular pipe is given by the formula:
A=π(D2)2
- For the first section (A1):
A1=π(D12)2=π(2.52)2=π(1.25)2=π×1.5625
- For the second section (A2):
A2=π(D22)2=π(9.762)2=π(4.88)2=π×23.8144
- According to the equation of continuity:
A1⋅V1=A2⋅V2
- Rearranging gives us:
V1V2=A2A1
- Substitute the areas calculated:
V1V2=A2A1=π×23.8144π×1.5625
- The π cancels out:
V1V2=23.81441.5625
- Performing the division:
V1V2=15.21
- Therefore, the ratio of the velocities V1 to V2 is:
V1:V2=15.21:1
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT File (MCQ)
5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Exemplar Problems (Subjective Questions))
5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Additional Exercises)
11 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
An ideal fluid flows through a pipe of circular cross section with diameters 5 cm and 10 cm as shown. The ratio of velocities of fluid at A and B is

View SolutionAn ideal fluid flows through a pipe of circular cross - section with diameters 5 cm and 10 cm as shown in the figure. The ratio of velocities of fluid at A and B is

View Solution
Knowledge Check
An ideal fluid flows through a pipe of circular cross section made of two sections with diameters 2.5 cm and 3.75 cm. The ratio of the velocities in the two pipes is
A9:4,B3:2,C√3:√2D√2:√3An ideal fluid flows through a pipe of circular cross-section made of two sections with diameters 2.5cm and 3.75cm. The ratio of the velocities in the two pipes is
A9:4B3:2C√3:√2D√2:√3An ideal fluid through a pipe of circular cross-section made of two sections with diameters 2.5cm and 3.75cm. The ratio of the velocities in the two pipes is
A9:4B3:2C√3:√2D√2:√3
An ideal fluid flows through a pipe of circular cross section of radius r at a speed v0. Now a viscous liquid is made to flow through the pipe at the same volume flow rate (measured in m3s–1). Find the maximum speed of a fluid particle in the pipe.
View SolutionIn streamline flow of liquid through a pipe of uniform cross sectional area, all stremlines are
View SolutionWater flows through a non-uniform tube of area of cross section A, B and C whose values are 25, 15 and 35cm2 resprectively. The ratio of the velocities of water at the sections A,B and C is
View SolutionAssertion : When an ideal fluid flows through a pipe of non-uniform cross-section, then pressure is more at that section where area is more if the pipe is horizontal.
Reason : According to Bernoulli's theorem speed at broader cross-section will be less.
View Solution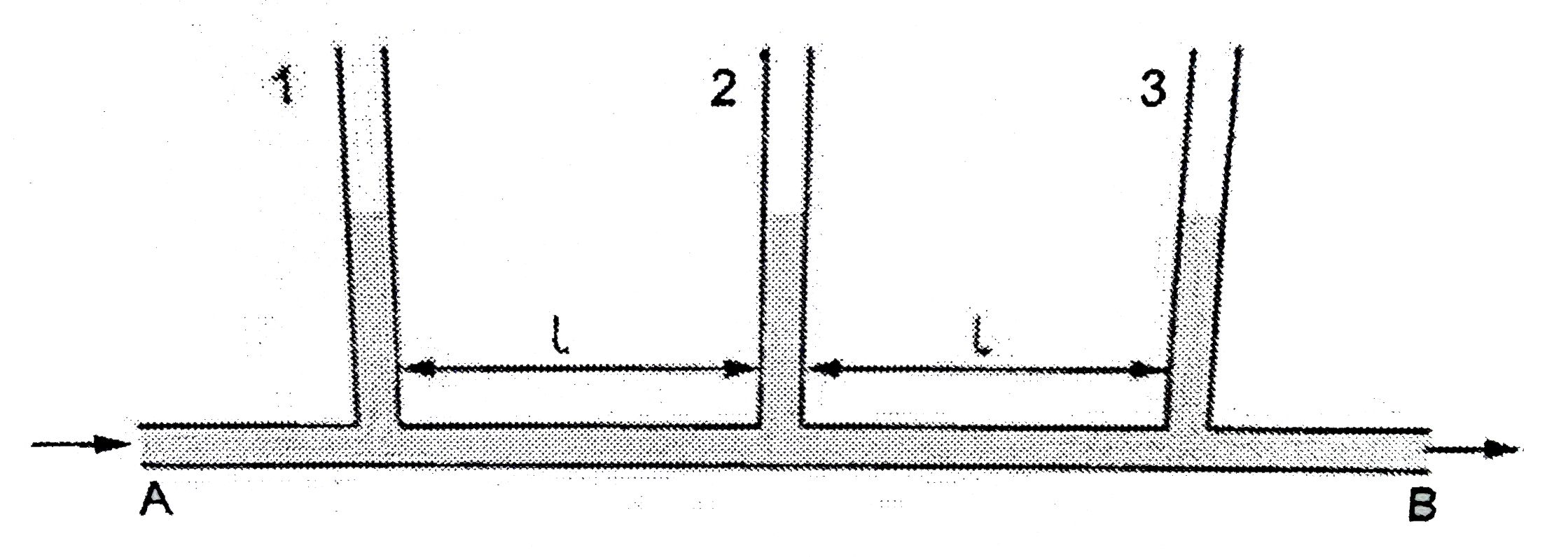
An ideal liqquid flows through the horizontal pipe AB, which is of uniform cross-section. The vertical pipes 1,2 and 3 equispaced. The liqudi levels in these pipes are at heightes h1,h2h3 respectively above AB. Liquid flows from A to B in AB.
View Solution
