An ideal gas consisting of rigid diatimic molecules goes through an adiabatic process process. How do the mean free path and the number of collisions of each molecule per second depend in this process on
(a) the volume ,
(b) the pressure ,
( c) the temperature ?
(a)
Thus and
But in an adiabatic process
constant
or Thus
(b)
But constant or or
Thus
( c)
But constant or
Thus
.
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Phase Transformations
35 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
An ideal gas goes through a polytropic process with exponent n. Find the mean free path λ and the number of collisions of each molecule per second v as a function of
(a) the volume V ,
(b) the pressure p ,
( c) the temperature T.
View SolutionHow does the mean free path λ and the number of collisions of each molecule per unit time v depend on the absolute temperature of an ideal gas undergoing
(a) an isochoric process ,
(b) an isobaric process ?
View Solution
Knowledge Check
The variation of pressure P with volume V for an ideal monatomic gas during an adiabatic process is hown in figure. At the magnitude of rate of change of pressure with volume is-
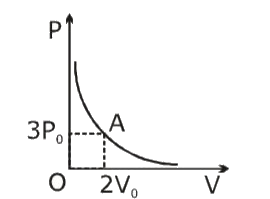 A3P05V0B5P03V0C3P02V0D5P02V0
A3P05V0B5P03V0C3P02V0D5P02V0During an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio CP/CV for the gas is
A43B2C53D32A mono-atomic ideal gas is compressed form volume V to V/2 through various process. For which of the following processes final pressure will be maximum:
AisobaricBisothermalCadiabaticDPV2= constant
As a result of some process the pressure of an ideal gas increases n−fold. How many times have the mean free path λ and the number of collisions of each molecule per unit time v changed and how, if the process is
(a) isochoric ,
(b) isothermal ?
View SolutionDetermine the molar heat capacity of a polytropic process through which an ideal gas consisting of rigid diatomic molecules goes and in which the number of collisions between the molecules remains constant
(a) in a unit volume ,
(b) in the total volume of the gas.
View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio CP/CV for the gas is
View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio CP/CV for gas is
View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature the ratio CpCv for the gas is
View Solution
