One end of a rod, enclosed in a thermally insulating sheath, is kept at a temperature T1 while the other, at T2. The rod is composed of two sections whose lengths are l1 and 12 and heat conductivity coefficients x1 and x2. Find the temperature of the interface.
Let T = temperature of the interface
Then heat flowing from left = heat flowing into right in equilibrium.
Thus k1T1−Tt1=k2T−T2l2 or T=(k1T1l1+k2T2l2)(k1l1+k2l2).
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Phase Transformations35videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
Similar Questions
Find the temperature distribution in a substance placed between two parallel plates kept at temperatures T1 and T2. The plate separation is l. The heat conductivity coefficient λ varies with temperature as 1/√T.
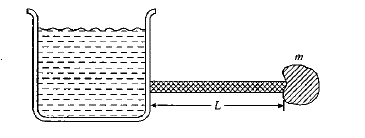
View SolutionFigure-4.13 shows a water tank at a constant temperature. T0 and a small bodyof mass m, and specific heat S at a temperature T1 . Given that T1<T0. A metal rod of length L, cross-sectional area A whose thermal conductivity is K is placed between the tank and the body to connect than. Find the temperature of body as a function of time. Given that the heat capacity of rod is negligible.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
One end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
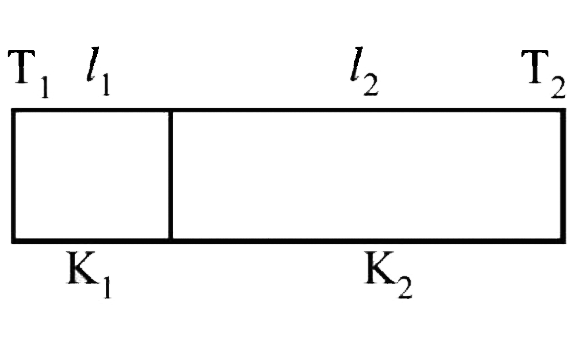 AK1l1T1+K2l2T2K1l1+K2l2BK2l2T1+K1l1T2K1l1+K2l2CK2l1T1+K1l2T2K2l1+K1l2DK1l2T1+K2l1T2K1l2+K2l1
AK1l1T1+K2l2T2K1l1+K2l2BK2l2T1+K1l1T2K1l1+K2l2CK2l1T1+K1l2T2K2l1+K1l2DK1l2T1+K2l1T2K1l2+K2l1 - Question 2 - Select One
One end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
A(k1l1T1+k2l2T2)(k1l1+k2l2)B(k2l2T1+k1l1T2)(k1l1+k2l2)C(k2l1T1+k1l2T2)(k2l1+k1l2)D(k1l2T1+k2l1T2)(k1l2+k2l1) - Question 3 - Select One
Two rods A and B are of equal lengths. Their ends of kept between the same temperature and their area of cross-section are A1 and A2 and thermal conductivities K1 and K2. The rate of heat transmission in the two rods will be equal, if
AK1A2=K2A1BK1A1=K2A2CK1=K2DK1A1=K2A2
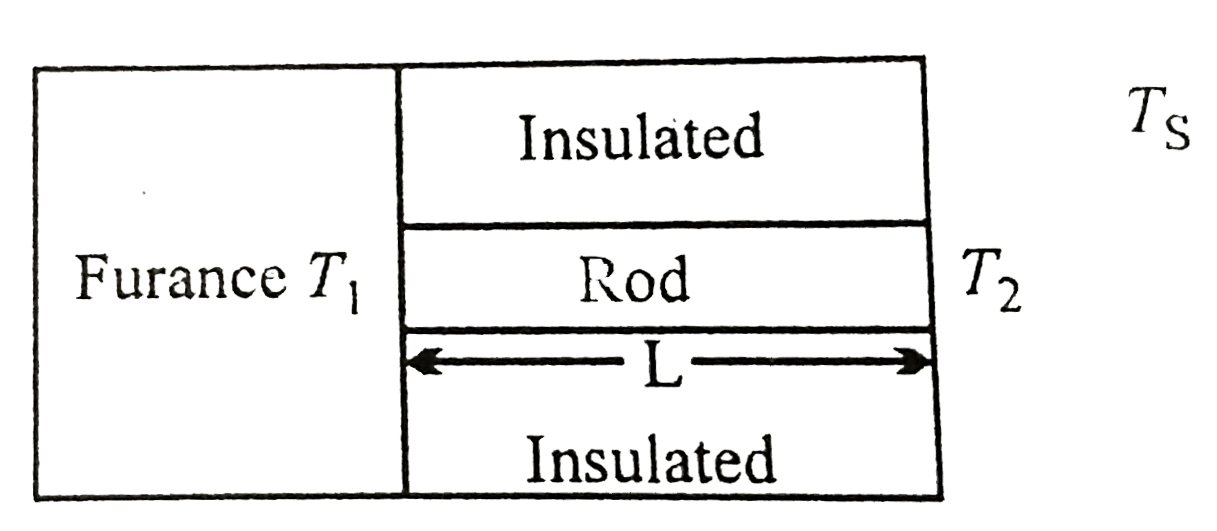
One end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
 View Solution
View SolutionFind the temperature distribution in a substance palced between two parallel plates kept at temperatures T1 and T2. The plate separation is equal to l, the heat conductivity coefficient of the substance x¯¯¯¯¯¯∝V¯¯¯T.
View SolutionThe ends of a metal rod are kept at temperatures θ1 and θ2 with θ2>θ1. The rate of flow of heat along the rod is directly proportional to
View SolutionHeat flows through two rods having same temperature difference at the ends. One rod is of length l1 and r1 and thermal conductivity K1 and the other rod of l2,r2 and K2 . The heat flow rate through the two rods will be equal, if
View SolutionHeat flows through two rods having same temperature difference at the ends. One rod is of length l1 and r1 and thermal conductivity K1 and the other rod of l2,r2 and K2 . The heat flow rate through the two rods will be equal, if
View Solution

