An ideal gas is enclosed in a cyclinder with a movable piston on top. The piston has mass of 8000g and an area of 5.00cm2 and is free to slide up and down, keeping the pressure of the gas constant. How much work is done as the temperature of 0.200mol of the gas is raised from 200∘C to 300∘C?
The correct Answer is:A
To solve the problem, we need to calculate the work done when the temperature of an ideal gas is raised while keeping the pressure constant. Here’s a step-by-step solution:
Step 1: Identify the given values
- Mass of the piston, m=8000g=8kg
- Area of the piston, A=5.00cm2=5.00×10−4m2
- Number of moles of gas, n=0.200mol
- Initial temperature, T1=200∘C=200+273.15=473.15K
- Final temperature, T2=300∘C=300+273.15=573.15K
Step 2: Calculate the change in temperature
ΔT=T2−T1=573.15K−473.15K=100K
Step 3: Use the ideal gas constant
The ideal gas constant R is given as:
R=8.31J/(mol K)
Step 4: Calculate the work done
The work done at constant pressure can be calculated using the formula:
W=nRΔT
Substituting the known values:
W=(0.200mol)×(8.31J/(mol K))×(100K)
W=0.200×8.31×100=166.2J
Final Answer
The work done as the temperature of the gas is raised from 200∘C to 300∘C is 166.2J.
---
- Mass of the piston, m=8000g=8kg
- Area of the piston, A=5.00cm2=5.00×10−4m2
- Number of moles of gas, n=0.200mol
- Initial temperature, T1=200∘C=200+273.15=473.15K
- Final temperature, T2=300∘C=300+273.15=573.15K
ΔT=T2−T1=573.15K−473.15K=100K
The ideal gas constant R is given as:
R=8.31J/(mol K)
The work done at constant pressure can be calculated using the formula:
W=nRΔT
Substituting the known values:
W=(0.200mol)×(8.31J/(mol K))×(100K)
W=0.200×8.31×100=166.2J
The work done as the temperature of the gas is raised from 200∘C to 300∘C is 166.2J.
Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Single Correct
27 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 More Than One Correct
6 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 1 Objective Questions
1 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
Similar Questions
An ideal gas is enclosed in a cylinder with a movable piston on top of it. The piston has a mass of 800 g and an area of 5.00cm2 and is free slide up and down, keeping the pressure of the gas constant. How much work is done on the gas as the temperature of 0.200 mol of the gas is raised from 20.0∘C to 300∘C ?
View SolutionA cylinder has a movable piston on its top. The piston has a mass of 7 kg and an area of 6×10−4m2. The piston can slide up and down, keeping the pressure of the ideal gas enclosed in the cylinder constant. What is the work done if the temperature of 0.5 mol of the gas in raised from 30∘C to 250∘C?[R=8.31Jmol−1K−1]
View Solution
Knowledge Check
An ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
A12π√MV0AγP0B12πAγP0V0MC12πV0MP0A2γD12π√A2γP0MV0
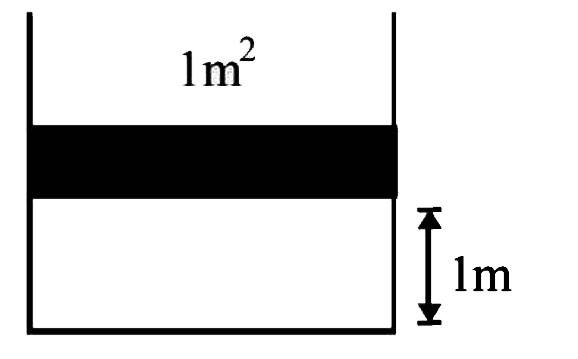
A diatomic gas is enclosed in a vessel fitted with massless movable piston. Area of cross section of vessel is 1m2. Initial height of the piston is 1m (see the figure). The initial temperature of the gas is 300K. The temperature of the gas is increased to 400K, keeping pressure constant, calculate the new height of the piston. The piston is brought to its initial position with no heat exchange. Calculate the final temperature of the gas. You can leave answer in fraction.
View SolutionSuppose there are N molecules each of mass m, of an ideal gas in a container. The x component of velocity of a molecule is denoted by ux. The gas is enclosed using a horizontal piston of area A as shown.

If the piston is moved so as to reduce the volume of gas by half, keeping the temperature of gas constant , we know from the gas law that the pressure will be doubled. On microscopic level the increase in pressure on the piston is because
View SolutionOne mole of an ideal gas (Cv,m=52R) at 300 K and 5 atm is expanded adiabatically to a final pressure of 2 atm against a constant pressure of 2 atm. Final temperature of the gas is :
View SolutionAn ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View SolutionTwo moles of a gas at 8.21 bar and 300 K are expanded at constant temperature up to 2.73 bar against a constant pressure of 1 bar. How much work (in Latm) is done by the gas?
(neglect the sign)
View Solution200cm2 of a ga at 800 mm pressure is allowed to expand till the pressure is 0.9 atm keeping ath temperature constant. Calculate the volume of the gas.
View SolutionOne mole of a gas is enclosed in a cylinde in a cyclinder and occupies a volume of 1.5L at a pressure 1.5 atm. It is subjected to strong heating due to which temperature of the gas increase according to the relation T=αV2, where α is a positive constant and V is volume of the gas.
a. Find the work done by air in increasing the volume of gas to 9L.
b. Draw the P−V diagram of the process.
c. Determine the heat supplied to the gas (assuming γ=1.5).
View Solution
