An ideal gas is taken round a cyclci thermodynamic process ABCA as shown if Fig. If the internal energy of the gas at point A is assumed zero while at B it is 50 J. The heat absorbed by the gas in the process BC is 90 J.
(a) What is the internal energy og the gas at point C ?
(b) How much heat energy is absorbed by the gas in the process AB?
(c ) Find the heat energy rejected or absorbed by the gas in the process CA.
(d) What is the net work done by the gas in the complete cycle ABCA ?
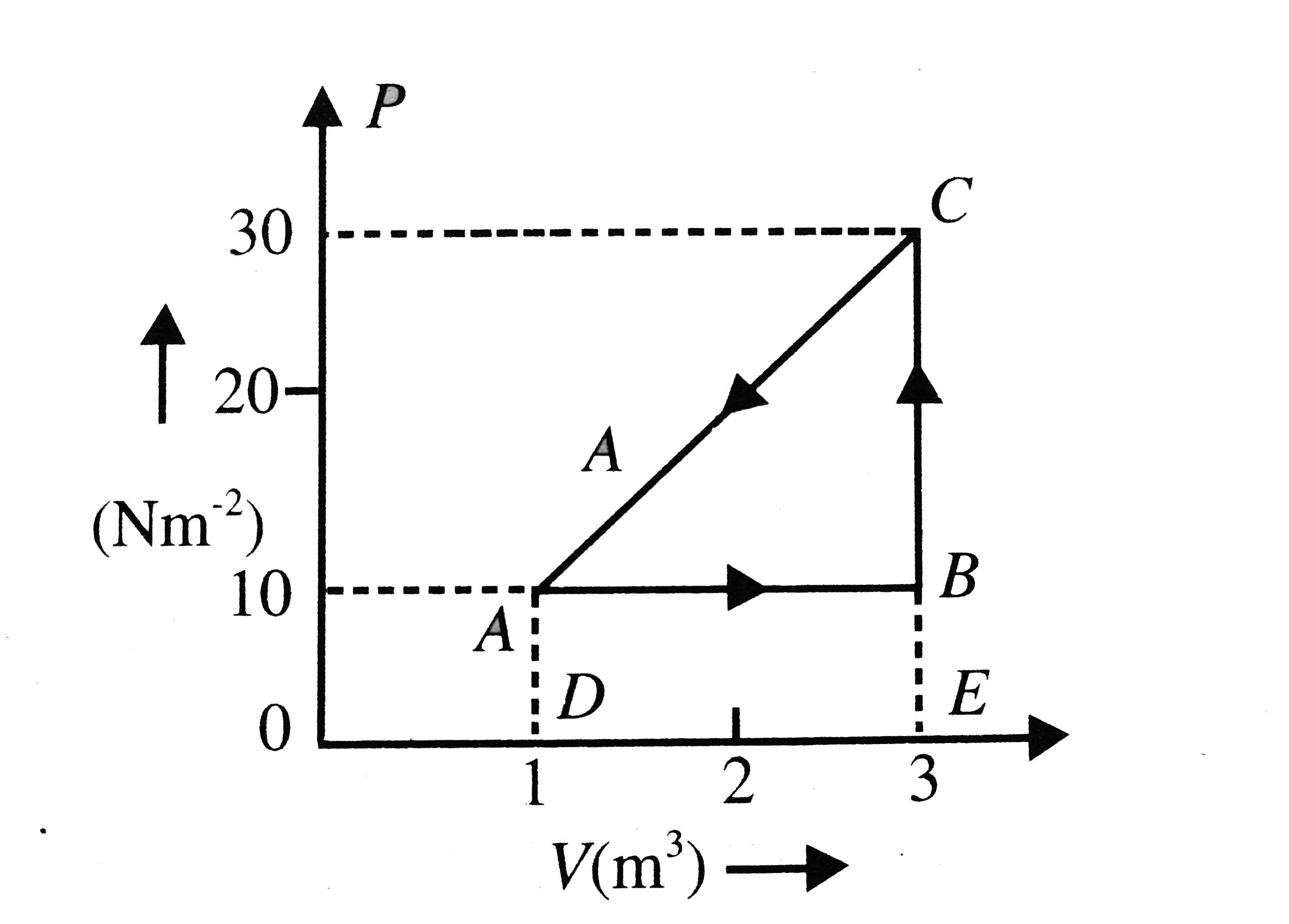
Given that UA=0,UB=50J and QBC=90J
Also PA=PB=10Nm−2,PC=300Nm−2,VA=1m3
and VB=VC=3m3
a. In process BC as volume of gas remains constant, work done by gas in this process is zero, thus
WBC=0
Heat abosrbed by the gas is QBC=90J. From the first law of thermodynamics.
(ΔU)BC=UC−UB=QBC−WBC=90J−0=90J
UC=(ΔU)BC+UB=90J+50J=140J
b. In process AB, we have
(ΔU)AB=UB−UA
=50−0=50J
work done is given as
WAB = area under AB in P - V diagram
= area of rectangle ABED
=AB×AD=(3m3=1m3)×10Nm−2
=20J
Thus heat abosrbed by the system is
QAB=(ΔU)AB+WAB=50+20=70J
c. For process CA
(ΔU)CA−UA−UC=0−140=−140J
Work done is given as
WCA= area ACED
= area of triangle ACB + area of rectangle ABED
1/2×AB×BC+AB×AD
=1/2×(3−1)m3×(30−10)Nm−2+20
=20+20=40J
In this process, the volume decreases, the work is done on the gas, Hence, the work done is negaitve,
Thus,
WCA=−40J
Thus heat rejected by the gas is
QCA=(ΔU)CA+WCA=−140−40=−180J
Net work done in the complete cyclic process ABCA is
W=area of triangleABC=12×2×20=20J
As the cycle is anticlockwise, net work is done on the gas.
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Solved Examples
14 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.1
20 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
Similar Questions
An ideal gas follows a cyclic process as shown in figure. Internal energy of gas at point A is 10 J while at B is 70 J. the heat absorbed by gas in BC is 120 J.
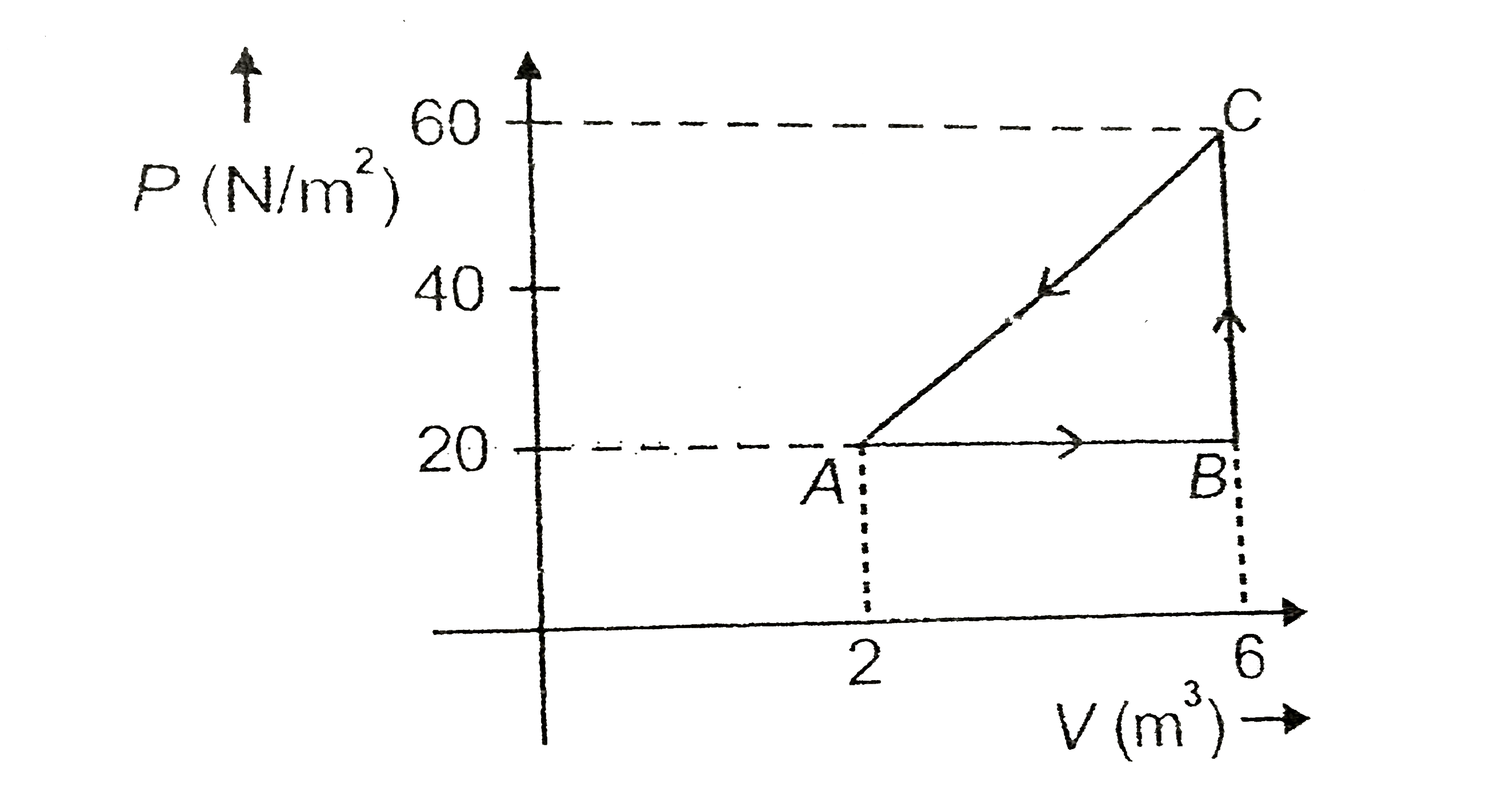
(a) How much heat is absorbed in process AB?
(b) Find heat energy rejected or absorbed by gas in process CA.
View SolutionA gas is taken through a cyclic process ABCA as shown in, if 2.4 cal of heat is given in the process, what is the value of J ?
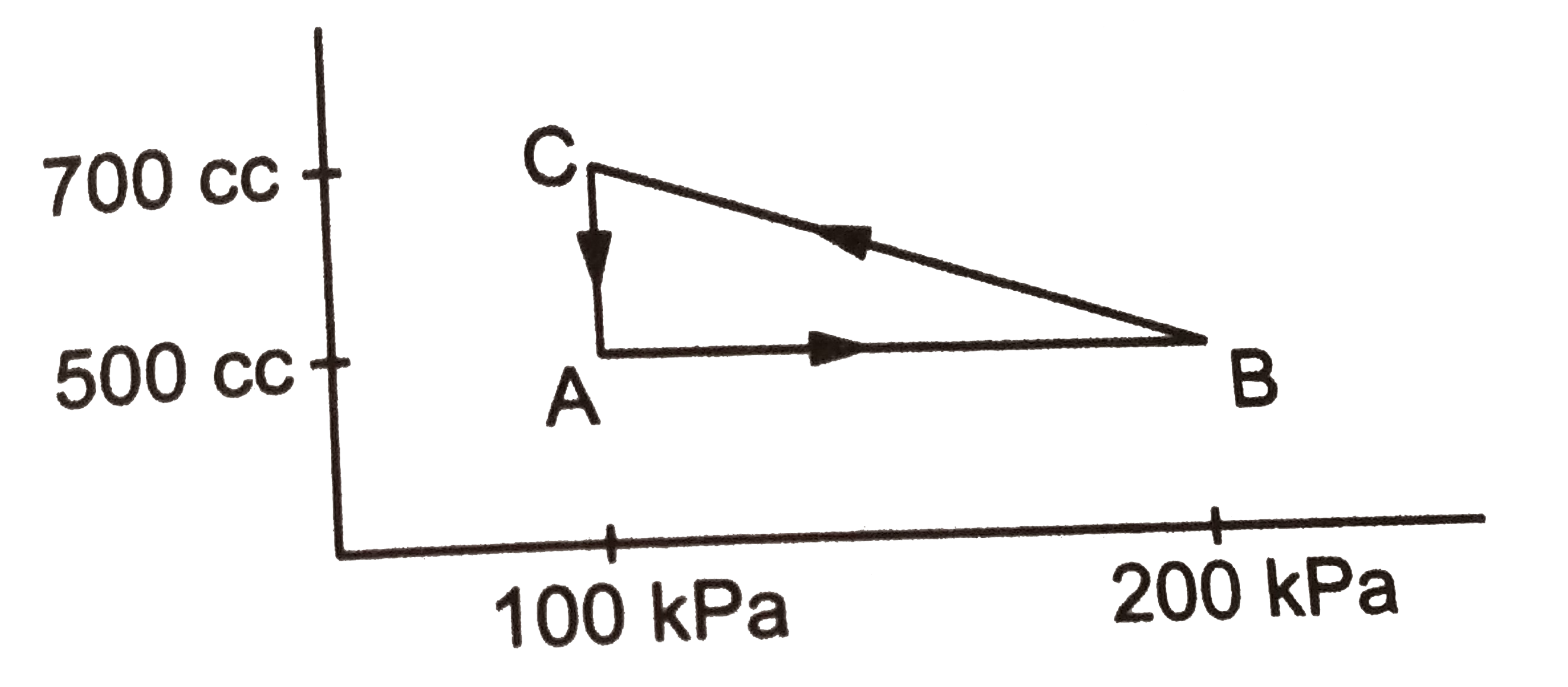
View Solution
Knowledge Check
In a cyclic process, the internal energy of the gas
AincreasesBdecreasesCremains constant,Dbecome zero.In a cyclic process, the internal energy of the gas
AIncreasesBDecreasesCRemains constantDBecomes zeroIf the internal energy of an ideal gas varies as U=2PV and the gas undergoes an expansion as shown below, then heat absorbed in the process will be :
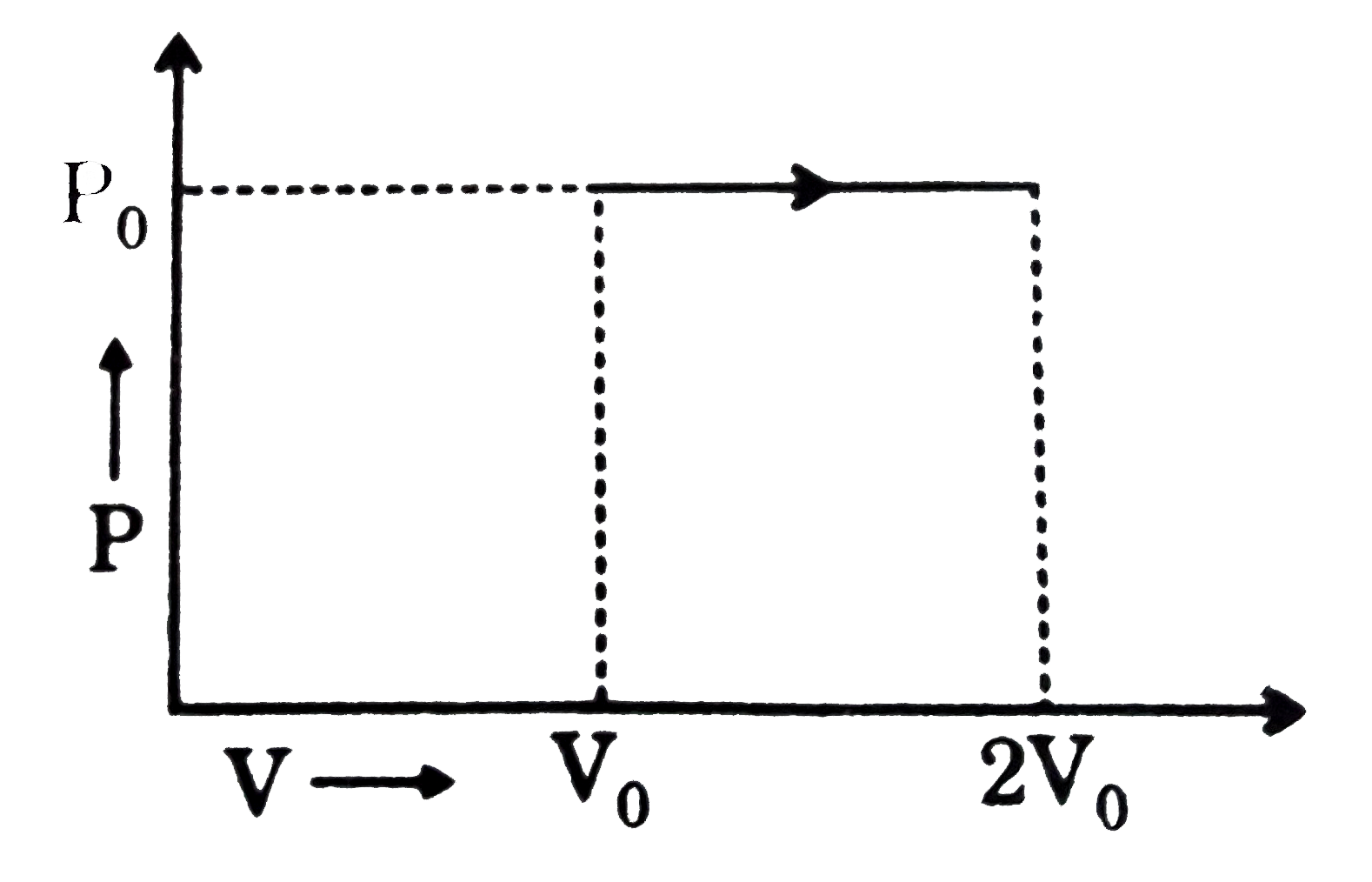 AP0V0BP0V02C3P0V0D32P0V0
AP0V0BP0V02C3P0V0D32P0V0
One mole of ideal monoatomic gas is taken round the cyclic process as shown in figure.
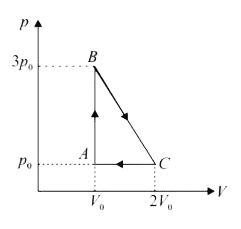
The heat rejected by the gas in the path is ………...and the heat absorbed by the gas in the path AB is ………...........
View SolutionMethod 5 of W
Heat taken from a gas in a process is 80 J and increase in internal energy of the gas is 20J. Find work done by the gas in the given process.
View SolutionAn ideal gas is taken through the process ABC as shown in figure. If the internal energy of the substance decreases by 10000J and a heat of 7159 cal is released by the system, calculate the value of meachanical equivalent of heat (J).
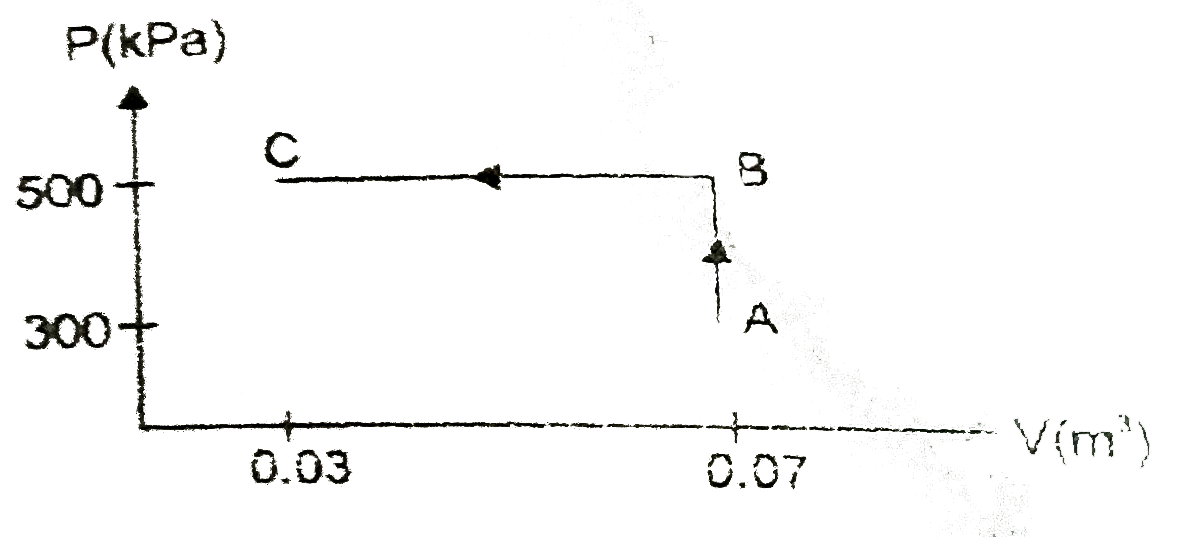
View Solution
A sample of an ideal gas is taken through the cyclic process abca and shown in the figure. The chagne in the internal energy of the gas along the path ca is −180J. The gas aborbs 250J of heat along the path ab and 60 J along the path bc. the work done by the along the path abc is:
View SolutionIn an adiabatic process 90 J of work is done on the gas. The change in internal energy of the gas is
View Solution
