The value of γ=CP/CV is 4/3 for an adaibatic process of an ideal gas for which internal energy U=K+nPV. Find the value of n (K is constant) :
The correct Answer is:3
PVγ= constant
PV4/3= constant
In (V4)+In(P3)= constant
4(dVV)=−3(dPP)
4P(dV)+3V(dP)=0
3(PdV+VdP)+PdV=0
For adiabatic process, dQ=0=dU+dW
dU+PdV
Compare Eps. (i) (ii), dU=3(PdV+VdP)
U=K+3PV
So, n=3
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Comprehension
Explore 56 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 9 Videos
Similar Questions
The internal energy of an ideal gas is sum of total kinetic energy of molecules. Consider an ideal gas in which the relation among U, P and V is U=2+3PVThe gas is
View SolutionFor an ideal gas the ratio of specific heats is CpCv=γ. The gas undergoes a polytropic process PV^(n) = a constant. Find the values of n for which the temperature of the gas increases when it rejects heat to the surrounding.
View Solution
Knowledge Check
The value of γ=CP/Cv is 4/3 for an adiabatic process of an ideal gas for which internal energy U=A+BPV. The value of B will be (A is a constant)
A2B3C4D5P-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
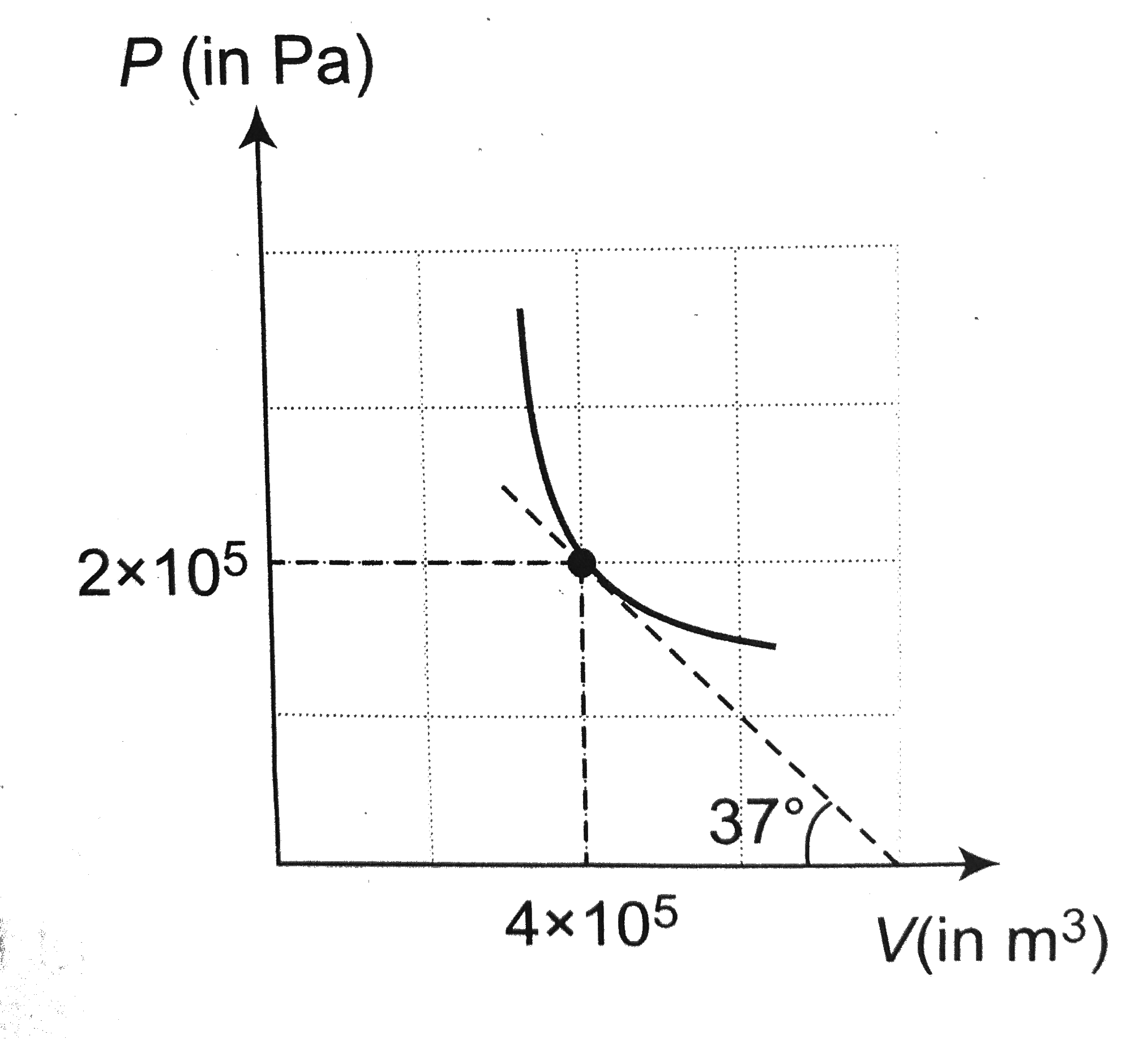 A34B−32C53D32
A34B−32C53D32In previous, Find the value of γ=CP/Cv:
A1.6B1.5C1.6D1.66
An ideal gas (CpCv=γ) is taken through a process in which the pressure and volume vary as (p=aVb. Find the value of b for which the specific heat capacity in the process is zero.
View SolutionThe relation between internal energy U, pressure P and volume V of a gas in an adiabatic process is
U=a+bPV where a and b are constant . What is the effective value of adiabatic constant γ.
View SolutionThe relation between U, p and V for an ideal gas in an adiabatic process is given by relation U=a+bpV. Find the value of adiabatic exponent (γ) of this gas.
View SolutionAn ideal gas with adiabatic exponent γ=43 undergoes a process in which internal energy is related to volume as U=V2 . Then molar heat capacity of the gas for the process is :
View SolutionAn ideal gas with adiabatic exponent (γ=1.5) undergoes a process in which work done by the gas is same as increase in internal energy of the gas. Here R is gas constant. The molar heat capacity C of gas for the process is:
View Solution