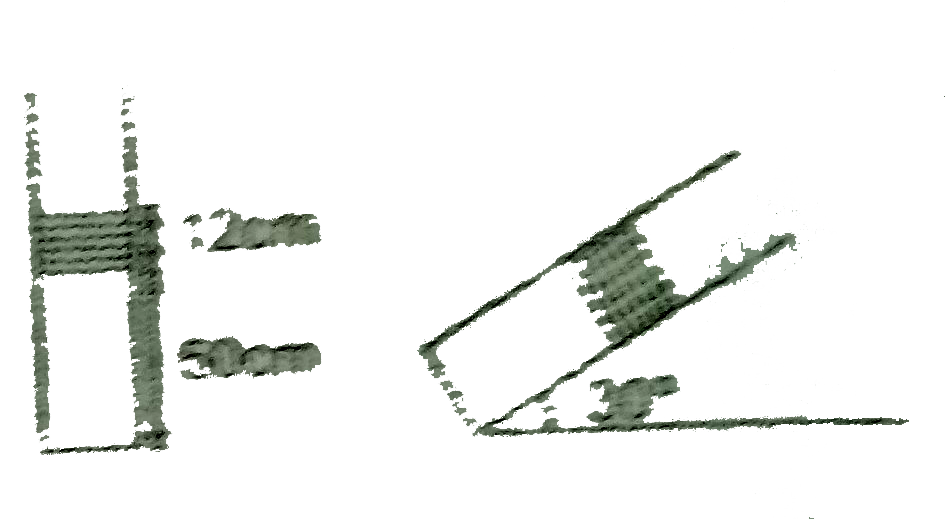
An ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals 76cm of mercury. The lenghts of the mercury column and the trapped air column are 20cm and 43cm respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60∘? Assume the temperature to remain constant.

Case ①: h0+l0=h1⇒76+20=h1
h1=96cm
Case ②: h0+l0cos60∘=h2⇒76+20×12=h2
h2=86cm
P1V1=P2V2
h1Al1=h2Al2
96×43=86l⇒l=48cm
Note: For explanation of symbols, consider alternative Solution: of previous problem.
Topper's Solved these Questions
Similar Questions
An ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to atmosphere (atmospheric pressure = 76 cm of Hg). The length of mercury and the trapped gas columns are 20 cm and 43 cm respectively. What will be the length of the gas column when the tube is titled slowly at constant temperature in a vertical plane through an angle of 60∘ ?
View SolutionAn ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to atmosphere (atmospheric pressure = 76 cm of Hg). The length of mercury and the trapped gas columns are 20 cm and 43 cm respectively. What will be the length of the gas column when the tube is titled slowly at constant temperature in a vertical plane through an angle of 60∘ ?
View Solution
Knowledge Check
- Question 1 - Select One
In a resonace tube experiment the lengths of the air columns for the first and second resonace differ by 25 cm . What is the wavelength of the sound in the tube ?
A20 cmB30 cmC40 cmD50 cm - Question 2 - Select One
Atmospheric pressure is 76 cm Hg and pressure of the gas is 77 cm Hg. Hence, height, 'h' of the mercury column in open arm is
A1 cmB113.6×980cmC153 cmD1×1.36×980 cm - Question 3 - Select One
When an air column in a tube open at both the ends is set into vibration with
AOdd harmonics are presentBSome harmonics are presentCAll harmonic are presentDEven harmonics are present
In given figure, an ideal gas is trapped between a mercury column and the closed end of a uniform vertical tube. The upper end of the tube is open to the atmosphere. Initially the lengths of the mercury column and the trapped air colume are 12cm and 50cm respectively. when the tube is titted solwly in a vertical plane through an angle of 30∘ with horizontal then the new length of air colume is x41m. Find x. Assuming the temperature to remains constant. (Patm=76cmofHg)
 View Solution
View SolutionThe atmospheric pressure at sea-level is equivalent to the pressure exerted by _____ cm mercury column at that place.
View SolutionA column of mercury of 10cm length is contained in the middle of a narrow horizontal 1m long tube which is closed at both the ends. Both the halves of the tube contain air at a pressure of 76 cm of mercury. By what distance will the column of mercury be displaced if the tube is held vertically?
View SolutionIf the length of the mercury column in a mercury barometer is 76 cm, what is the equivalent height of the water column ?
View SolutionWhat will be the length of mercury column in a barometer tube when the atmospheric pressure is x cm of mercury and the tube is inclined at an angle ϕ with the vertical direction ?
View Solution

