An ideal gas undergoes an expansion from a state with temperature T1 and volume V1 through three different polytropic processes A,B and C as shown in the P−V diagram. If |ΔEA|,|ΔEB| and |ΔEC| be the magnitude of changes in internal energy along the three paths respectively, then :

|ΔEA|<|ΔEB|<|ΔEC| if temperature in every process decreases
|ΔEA|>|ΔEB|>|ΔEC| if temperature in every process decreases
|ΔEA|>|ΔEB|>|ΔEC| if temperature in every process increases
|ΔEB|<|ΔEA|<|ΔEC| if temperature in every process increases
The correct Answer is:A, C
Initial state is same for all the three processes (say initial internal energy =E0).
In the final state, VA=VB=VC
and PA>PB>PC
PAVA>PBVB>PCVC
EA>EB>EC
If T1<T2, then E0>Ef for all the three processes and hence (E0−EA)<(E0−EB)<(E0−EC)
|ΔEA|<|ΔEB|<|ΔEC|
If T1<T2, then E0<Ef for all three processes and hence (EA−E0)>(EB−E0)>(EC−E0)
|ΔEA|>|ΔEB|>|ΔEC|
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Comprehension
56 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Single Correct
140 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
Similar Questions
One mole of an ideal gas is taken from state A to state B by three different processes (a) ACB, (b) ADB and (c ) AEB as shown in the P−V diagram. The heat absorbed by the gas is

View SolutionA gas is expanded from volume V0 to 2V0 under three different processes, as shown in the figure. Process 1 is isobaric process, process 2 is isothermal and process 3 is adiabatic. Let ΔU1,ΔU2 and ΔU3 be the change in internal energy of the gas in these three processes. Then
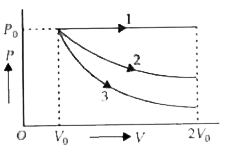
View Solution
Knowledge Check
Let ΔU1 and ΔU2 be the changes in internal energy of an ideal gas in the processes A and B then
AΔU1>ΔU2BΔU1=ΔU2CΔU1<ΔU2DΔU1≠ΔU2An ideal gas goes from state A to state B via three different processes as indicated in the P-V diagram. If Q1,Q2,Q3 indicate the heat absorbed by the gas along the three processes and ΔU1,ΔU2,ΔU3 indicate the change in internal energy along the three processes respectively, then
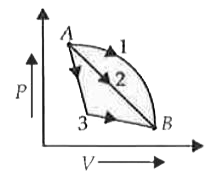 AQ1>Q2>Q3 and ΔU1=ΔU2=ΔU3BQ1>Q2>Q3 and ΔU1=ΔU2=ΔU3CQ1=Q2=Q3 and ΔU1>ΔU2>ΔU3DQ3>Q2>Q1 and ΔU1>ΔU2>ΔU3
AQ1>Q2>Q3 and ΔU1=ΔU2=ΔU3BQ1>Q2>Q3 and ΔU1=ΔU2=ΔU3CQ1=Q2=Q3 and ΔU1>ΔU2>ΔU3DQ3>Q2>Q1 and ΔU1>ΔU2>ΔU3An ideal gas goes from State A to state B via three different process as indicate in the P−V diagram.
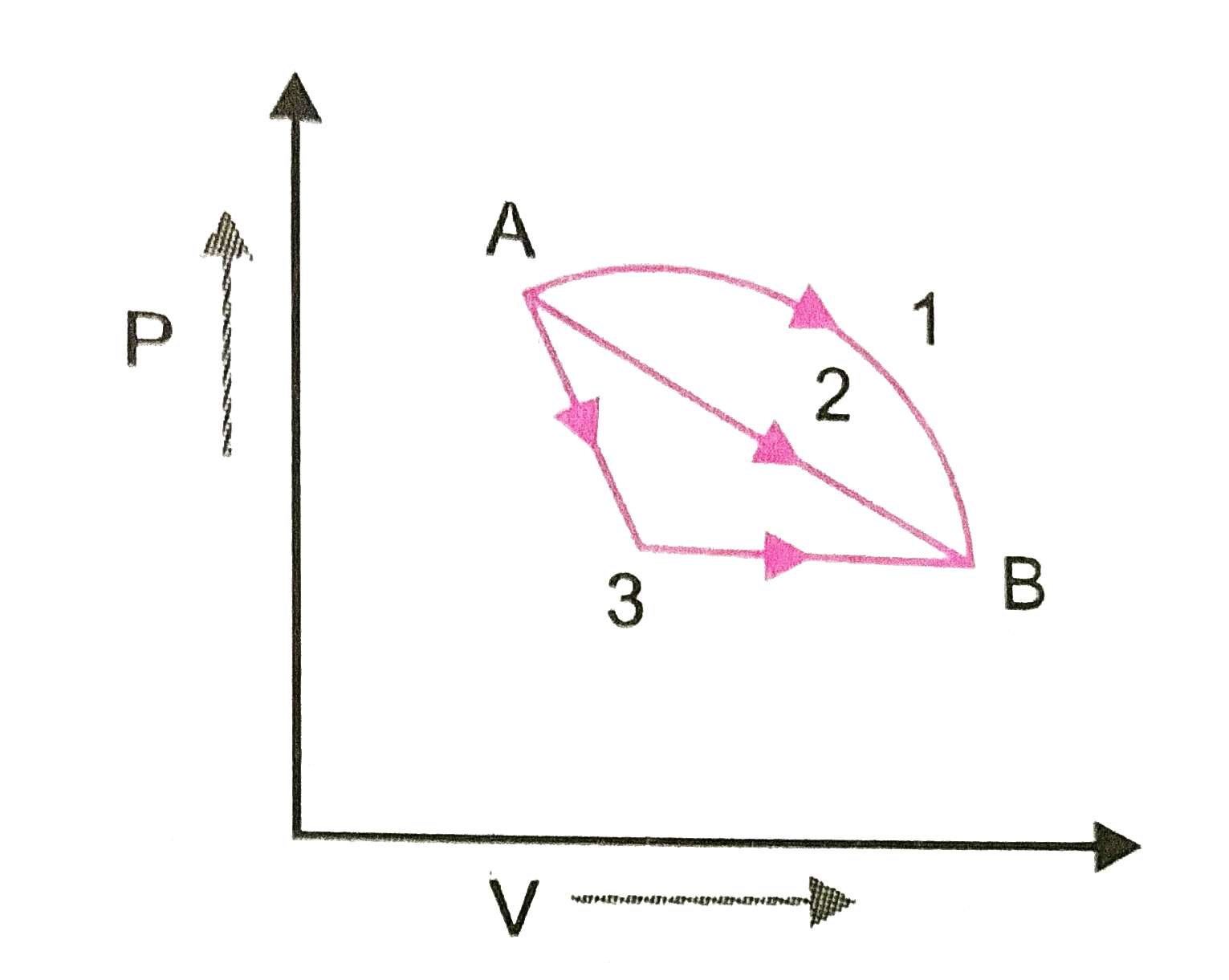
If Q2,Q3 indicates the heat absorbed by the gas along the three processes and ΔU1,ΔU2,ΔU3 indicates the change in internal energy along the three processes respectively, thenAQ1>Q2>Q3 and ΔU1=δU2=ΔU3BQ3>Q2>Q1 and ΔU1=ΔU2=ΔU3CQ1=Q2=Q1 and ΔU1>ΔU2>ΔU3DQ3>Q2Q1 and ΔU1>ΔU2>ΔU3
A system is changed from state A to state B by one path and from B to A by another path. If ΔE1 and ΔE2 are the corresponding changes in internal energy, then
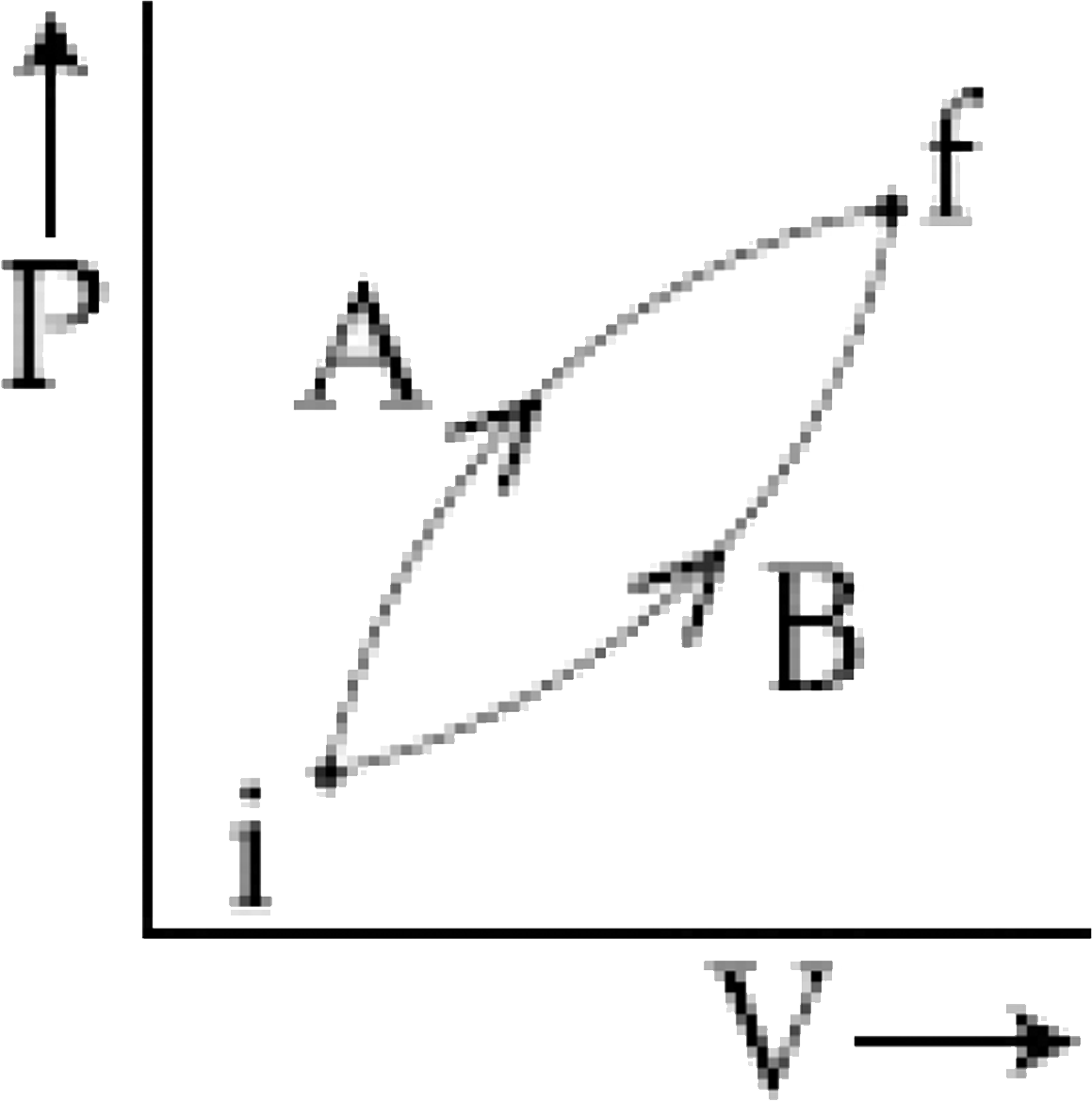
View SolutionFollowing figure shows two process A and B for a gas. If ΔQA and ΔQB are the amount of heat absorbed by the system in two case, and ΔUA and ΔUB are changes in internal energies, respectively, then :
View SolutionOne mole of an ideal gas is taken from state A to state B by three different processes (a) ACB, (b) ADB and (c ) AEB as shown in the P−V diagram. The heat absorbed by the gas is

View SolutionIn figure, three isothermal processes are shown for the same gas and for same change in volume (Vi−Vf) but at different temperature. If ΔQ1,ΔQ2, and ΔQ3 are the heat transferred in the respective process, then
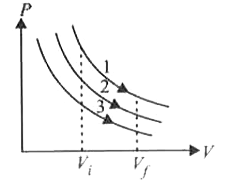
View SolutionA system is changed from state A to state B by one path and from B to A by another path. If ΔE1 and ΔE2 are the corresponding changes in internal energy, then
View Solution
