An ideal gas (whose CpCv=λ, and internal energy U at absolute zero temp. is equal to zero) undergoes a reversible adiabatic compression. If U,p,V,T Represent the internal energy, pressure, volume and temperature respectively of the ideal gas, then
UVλ =const
Upλ =const
VU1λ−1 =const
TVλ−1 =const
To solve the problem, we need to analyze the behavior of an ideal gas undergoing reversible adiabatic compression. Here's a step-by-step solution:
Step 1: Understand the properties of an ideal gas
An ideal gas follows the ideal gas law, which is given by:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the universal gas constant, and T is temperature.
Step 2: Recognize the conditions of adiabatic processes
For a reversible adiabatic process, the relationship between pressure and volume can be expressed as:
PVγ=constant
where γ=CpCv is the heat capacity ratio.
Step 3: Relate the ideal gas law to the adiabatic condition
From the ideal gas law, we can express pressure P in terms of volume V and temperature T:
P=nRTV
Substituting this into the adiabatic condition gives:
(nRTV)Vγ=constant
This simplifies to:
nRTVγ−1=constant
Step 4: Express the relationship in terms of temperature and volume
From the equation derived in Step 3, we can rearrange it to isolate T:
TVγ−1=constantnR
This implies that:
TVγ−1=constant
Step 5: Conclusion
Thus, we conclude that during a reversible adiabatic compression of an ideal gas, the product of temperature T and volume raised to the power of γ−1 remains constant:
TVγ−1=constant
Final Answer
The correct relationship that holds true for the ideal gas undergoing reversible adiabatic compression is:
TVγ−1=constant
---
An ideal gas follows the ideal gas law, which is given by:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the universal gas constant, and T is temperature.
For a reversible adiabatic process, the relationship between pressure and volume can be expressed as:
PVγ=constant
where γ=CpCv is the heat capacity ratio.
From the ideal gas law, we can express pressure P in terms of volume V and temperature T:
P=nRTV
Substituting this into the adiabatic condition gives:
(nRTV)Vγ=constant
This simplifies to:
nRTVγ−1=constant
From the equation derived in Step 3, we can rearrange it to isolate T:
TVγ−1=constantnR
This implies that:
TVγ−1=constant
Thus, we conclude that during a reversible adiabatic compression of an ideal gas, the product of temperature T and volume raised to the power of γ−1 remains constant:
TVγ−1=constant
The correct relationship that holds true for the ideal gas undergoing reversible adiabatic compression is:
TVγ−1=constant
Topper's Solved these Questions
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Numerical MCQs Single Options Correct
42 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Advance MCQs with One or More Options Correct
10 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Discussion Question
17 Videos
- PHOTOELECTRIC EFFECT AND MATTER WAVESBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - PHOTOELECTRIC EFFECT AND MATTER WAVESEXERCISE - Unsolved numerical problems
42 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
Similar Questions
Knowledge Check
If P, V, M, T and R are symbols of pressure, volume, molecular weight, temperature and Gas contstant, what is the equation of density of ideal gas
ARTPMBPRTCMVDPMRTThe internal energy (U), pressure (P) and volume (V) of an ideal gas are related as U=3PV+4. The gas is :-
ADiatomic onlyBPolyatomic onlyCEither monoatomic or diatomicDEither monoatomic or diatomicDuring a reversible adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio CPCV for the gas is
A3/2B7/2C5/3D9/7
The internal energy(U) ,pressure (P) and volume (V) of an ideal gas are related as U=3PV+4 .The gas is:
View SolutionThe quantity 2UfkT represents (where U= internal energy of gas)
View SolutionAn ideal gas with adiabatic exponent γ undergoes a process in which internal energy depends on volume
as U=aVα then select the correct statement .
View SolutionAn ideal gas in thermally insulated vessel at internal (pressure)=P1,(volume)=V1 and absolute temperature=T1 expands irreversiby against zero external, pressure , as shown in the diagram,
The final internal pressure, volume and absolute temperature of the gas are p2,V2andT2, respectively . For this expansion

View SolutionAn ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
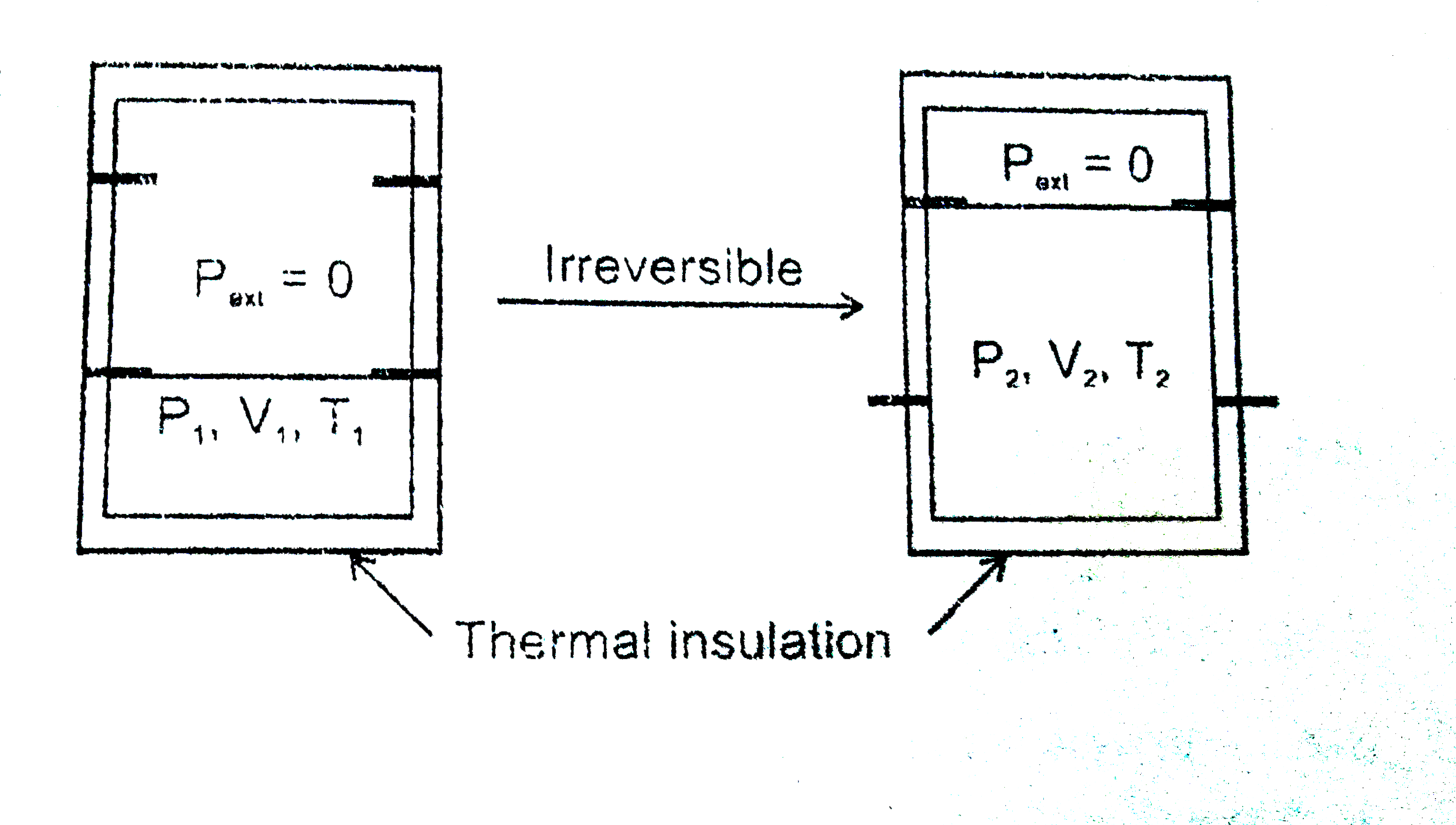
View Solution
