An ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
(a) 4Mgk
(b) 2Mgk
(c) Mgk
(d) Mg2k
The correct Answer is:B
To find the maximum extension in the spring when a block of mass M is attached to it and released from rest, we can use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Understand the Forces Acting on the Block
When the block is released, two main forces act on it:
- The gravitational force Fg=Mg acting downwards.
- The spring force Fs=kx acting upwards when the spring is stretched by an amount x.
Step 2: Set Up the Energy Conservation Equation
At the maximum extension of the spring, the kinetic energy of the block will be zero (it momentarily stops). Thus, the potential energy lost due to gravity will equal the potential energy stored in the spring.
The work done by gravity as the block moves down by a distance x is:
Wg=−Mgx
The potential energy stored in the spring when it is stretched by x is:
Ws=12kx2
Step 3: Apply Conservation of Energy
According to the conservation of energy:
Work done by gravity+Work done by spring=0
This gives us:
−Mgx+12kx2=0
Step 4: Rearrange the Equation
Rearranging the equation leads to:
12kx2=Mgx
Step 5: Solve for x
To solve for x, we can rearrange the equation:
12kx2−Mgx=0
Factoring out x:
x(12kx−Mg)=0
This gives us two solutions:
1. x=0 (the trivial solution)
2. 12kx−Mg=0 which simplifies to:
12kx=Mg⇒x=2Mgk
Conclusion
Thus, the maximum extension in the spring is:
x=2Mgk
When the block is released, two main forces act on it:
- The gravitational force Fg=Mg acting downwards.
- The spring force Fs=kx acting upwards when the spring is stretched by an amount x.
At the maximum extension of the spring, the kinetic energy of the block will be zero (it momentarily stops). Thus, the potential energy lost due to gravity will equal the potential energy stored in the spring.
Wg=−Mgx
The potential energy stored in the spring when it is stretched by x is:
Ws=12kx2
According to the conservation of energy:
Work done by gravity+Work done by spring=0
This gives us:
−Mgx+12kx2=0
Rearranging the equation leads to:
12kx2=Mgx
To solve for x, we can rearrange the equation:
12kx2−Mgx=0
Factoring out x:
x(12kx−Mg)=0
This gives us two solutions:
1. x=0 (the trivial solution)
2. 12kx−Mg=0 which simplifies to:
12kx=Mg⇒x=2Mgk
Thus, the maximum extension in the spring is:
x=2Mgk
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives(multiple Correct)
3 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (assertion-reasoning)
1 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer
14 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A sping of spring constant k is attached to the ceiling. A block of mass M is attached to its lower end and is released suddenly.
(ii) Find its speed at the instant it passes throught the equilibrium position.
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View Solution
Knowledge Check
An ideal spring with spring - constant K is bung from the colling and a block of mass M is attached to its lower end the mass is released with the spring initally unstetched . Then the maximum exlemsion in the spring is
A4MgKB2MgKCMgKDMg4KAn ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is
A4mgkB2MgkCMgkDMg2kA block of mass m attached in the lower and vertical spring The spring is hung from a calling and force constant value k The mass is released from rfest with the spring velocity unstrached The maximum value praduced in the length of the spring will be
AMg/kB2Mg/kC4Mg/kDMg/2k
spring of force constant k clamped rigidly at onoe end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?

View SolutionA block of mass 2M is attached to a massless spring with spring-constant k. This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are a1a2 and a3 as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is x0 Which of the following option(s) is(are) correct? [g is the acceleration due to gravity. Neglect friction]
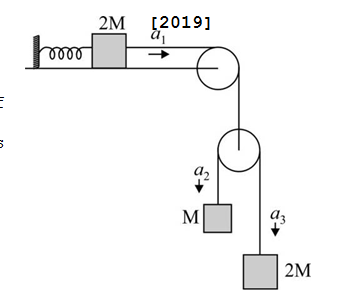
View SolutionIn the shown diagram mass of A is m and that of B is 2 m. All the surfaces are smooth. System is released from rest with spring unstretched. Then, the maximum extension (xm) in spring will be:

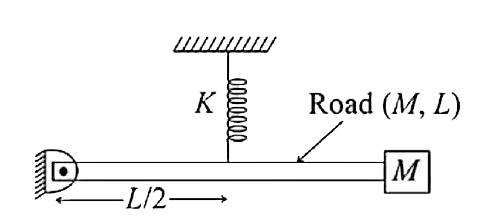
View SolutionA rod of mass 'M' and length'
L' is hinged about one end and a
particle of mass 'M' is
attached to its other end If it is
kept horizontal with the help of
a spring of spring constant 'K'
as shown in fig. find the
extension in spring :-
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View Solution
