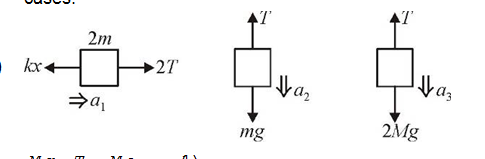
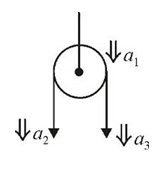
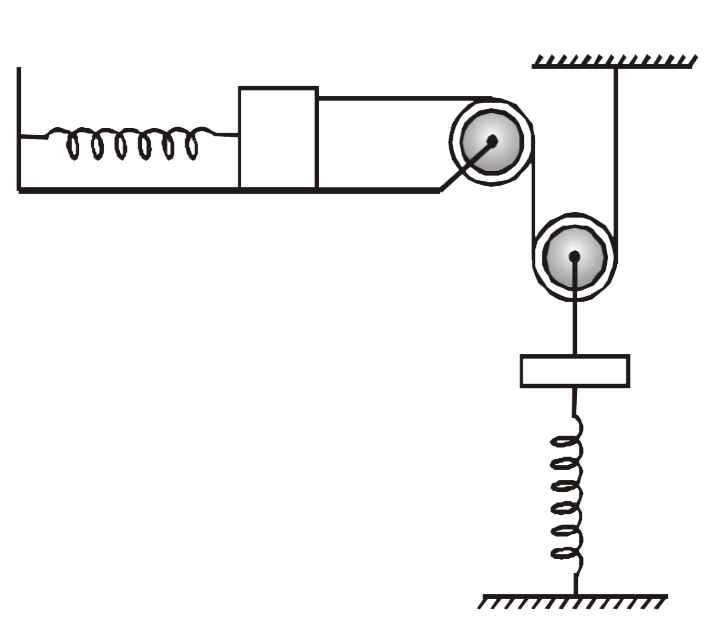
A block of mass 2M is attached to a massless spring with spring-constant k. This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are and as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is Which of the following option(s) is(are) correct? [g is the acceleration due to gravity. Neglect friction]
![A block of mass 2M is attached to a massless spring with spring-constant k. This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are a(1)a(2) and a(3) as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is x(0) Which of the following option(s) is(are) correct? [g is the acceleration due to gravity. Neglect friction]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/VMC_PHY_XI_WOR_BOK_03_C11_E05_023_Q01.png)
At an extension of of the spring, the magnitude of acceleration of the block connected to the spring is
When spring achieves an extension of for the first time, the speed of the block connected to the spring is
The correct Answer is:A
...(1)
...(2)
...(3)
From (1) and
implies ...(4)
,[Maximum elongation=2A]
Correct answer is (A)
Similar Questions
An ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View Solution
Knowledge Check
An ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
A(a) 4MgkB(b) 2MgkC(c) MgkD(d) Mg2kA 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)
 AzeroB10m/s2 , upwardsC10m/s2 downwardsD5m/s2 upwards
AzeroB10m/s2 , upwardsC10m/s2 downwardsD5m/s2 upwardsA block of mass m is attached with a massless spring of force constant k. The block is placed over a fixed rought inclined surface for which the coefficient of friction is μ=34 . The block of mass m is initially at rest . The block is mass M is released from rest with spring in unstretched state. The minimum value of M required to move the block up the plane is ( neglect mass of string and pulley and friction in pulley )
 A35mB45mC65mD32m
A35mB45mC65mD32m
A block of mass m attached in the lower and vertical spring The spring is hung from a calling and force constant value k The mass is released from rest with the spring initially unstreched The maximum value of extension produced in the length of the spring will be
View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
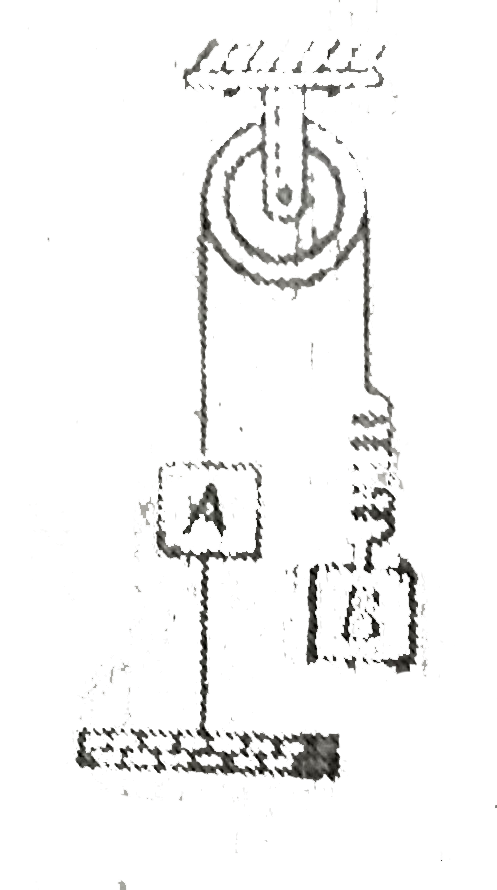
View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
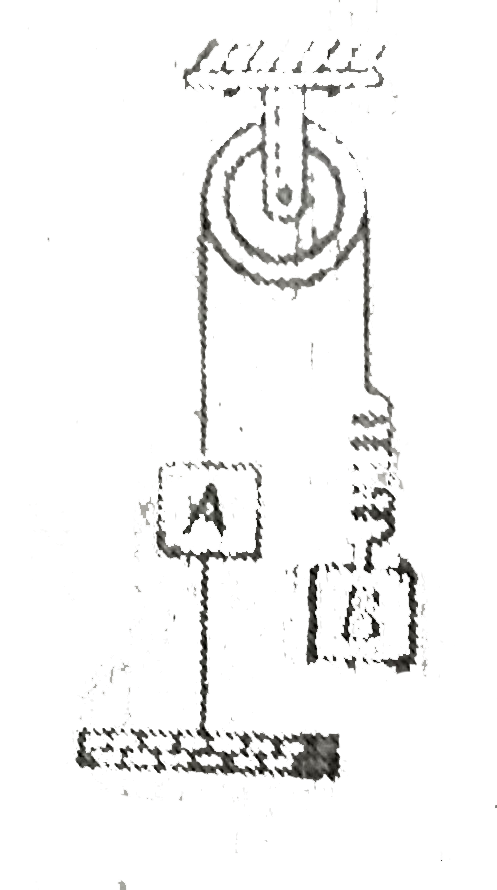
View SolutionA 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)

View SolutionIn the figure shown, the system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N/m.
Maximum speed of the block placed horizontally is:
View Solution
