An inductor and two capacitors are connected in the circuit as show in Fig Initially capacitor A has no charge and capacitor B has CV charge. Assume that the circuit has no resistance at all. At t=0, switch S is closed, then [given
LC=2π2×104S2 and Cv=100mC]
![An inductor and two capacitors are connected in the circuit as show in Fig Initially capacitor A has no charge and capacitor B has CV charge. Assume that the circuit has no resistance at all. At t = 0, switch S is closed, then [given LC = (2)/(pi^(2) xx 10^(4)) S^(2) and Cv = 100 mC]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V05_C04_E01_098_Q01.png)
when current in the circuit is maximum, charge on each capacitor is same
when current in the circuit is maximum, charge on capacitor A is twice the charge on capacitor B
q=50(1+cos100πt)mC, where q is the charge on capacitor B at time t
q=50(1−cos100πt)mC, where q is the charge on capacitor B at time t
The correct Answer is:A, C
Let at any time, charge and current in the circuit wire are as shows.

I=dq1dt
Applying kirchoff's law,
CV−q1C−q1C−LdIdt=0⇒CV−2q1LC=Ld2q1dt2
⇒d2q1dt2=−2LC(q1−CV2)
⇒q1−CV2=Asin(ωt+δ) (i)
where ω=√2LC=100πrad/s
At t=0, q1=0⇒0−CV2=Asinδ (ii)
Differentiating (i), dq1dt−0=Aωcos(ωt+δ)
⇒I=Aωcos(ωt+δ)
At t=0,I=0⇒0=Aωcosδ⇒δ=π2
From (ii), A=−CV2
From (i), q1=CV2−CV2sin(ωt+π2) (iv)
⇒q1=CV2(1cos100πt)mC
Now q2=CV−q1=CV2(1+cosωt) (v)
=50(1+cosωπt)
From (ii), I=−Aωsinωt
Current in the circuit is maximum for ωt=π2⋅
And for ωt=π2, we see from (iv) and (v) that q1=q2=CV2
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (linked Compreshension)
36 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (single Correct )
65 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
Knowledge Check
In the given LC circuit if initially capacitor C has change Q on it and 2C has charge 2Q. The polarities are as shown in the figure. Then after closing the switch s at t=0
 Aenergy will get equally distributed in both the capacitor just after closing the switchBInitial rate of growth of current in inductor will be 2Q/3CLCMaximum energy in the inductor will be 3Q2/2CDNone of these
Aenergy will get equally distributed in both the capacitor just after closing the switchBInitial rate of growth of current in inductor will be 2Q/3CLCMaximum energy in the inductor will be 3Q2/2CDNone of theseIn the circuit shown in fig. when the switch is closed, the capacitor charges with a time constant
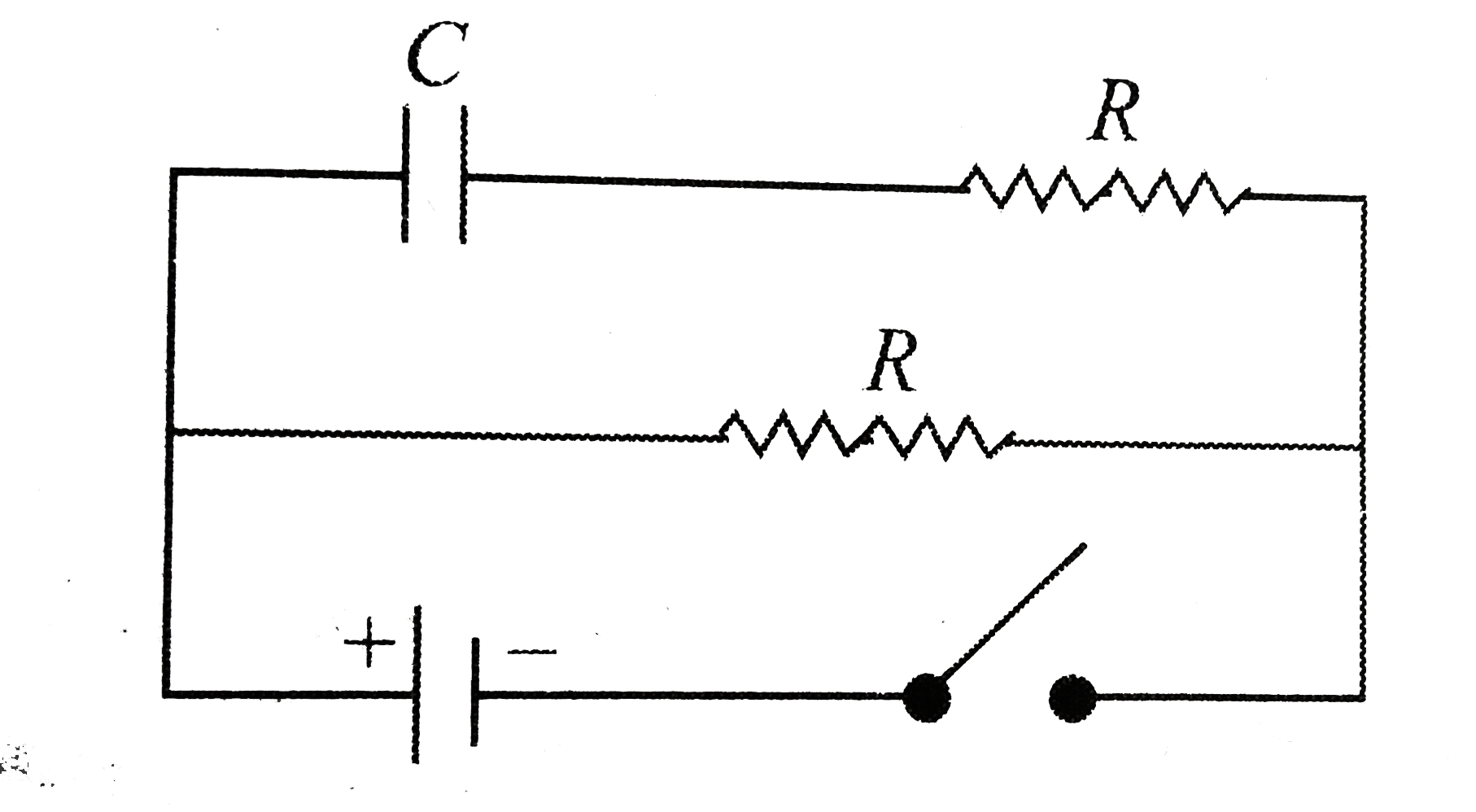 ARCB2 RCC12RCDRC log2
ARCB2 RCC12RCDRC log2In the given LC circuit,if initially capacitor C has charge Q on it and 2C has charge 2Q. The polar ar as shown in figure. Then after closing switch S and t=0
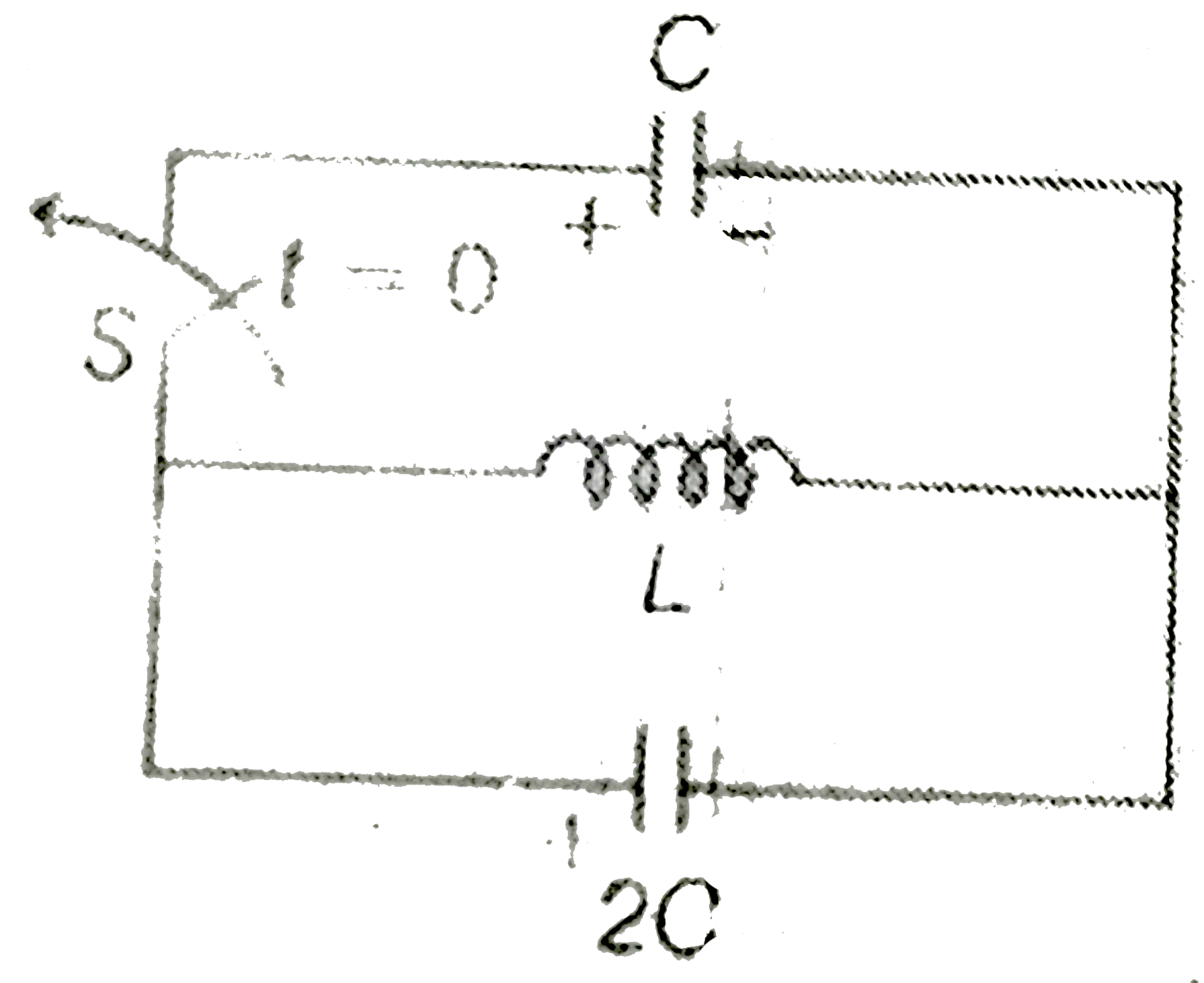 Aenergy will get equally distributed in both the capacitors ust after closing the switchBinitial rate of groqth of current in inductor will be 2Q/3CLCmaximum energy in the inductor will be 3Q2/2CDnone of these
Aenergy will get equally distributed in both the capacitors ust after closing the switchBinitial rate of groqth of current in inductor will be 2Q/3CLCmaximum energy in the inductor will be 3Q2/2CDnone of these
The switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
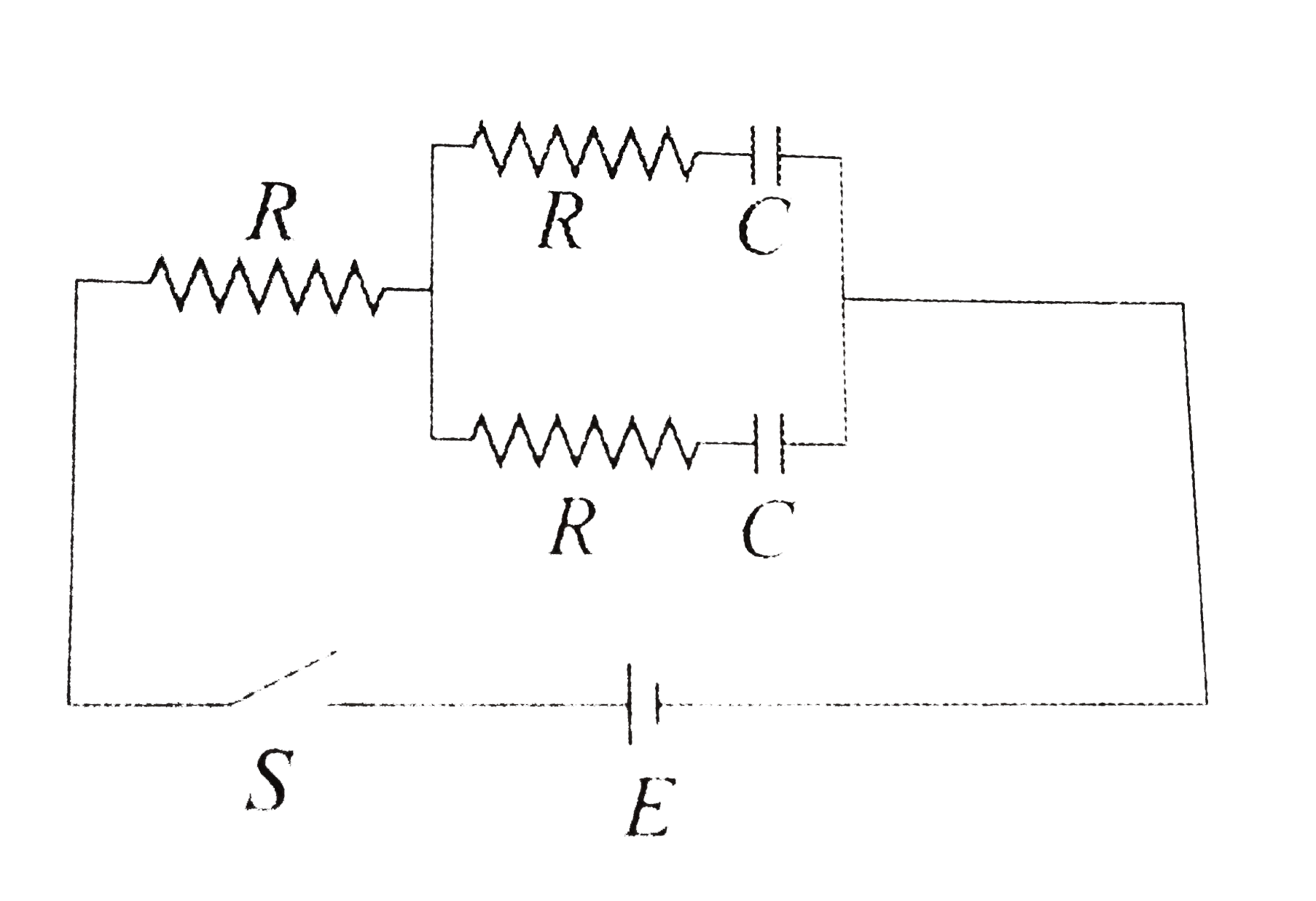
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant

View SolutionThe switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is

View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant

View SolutionInitially capacitor is uncharged at t=0 switch is closed. Charge on capacitor when current in the circuit is 10% of maximum current :
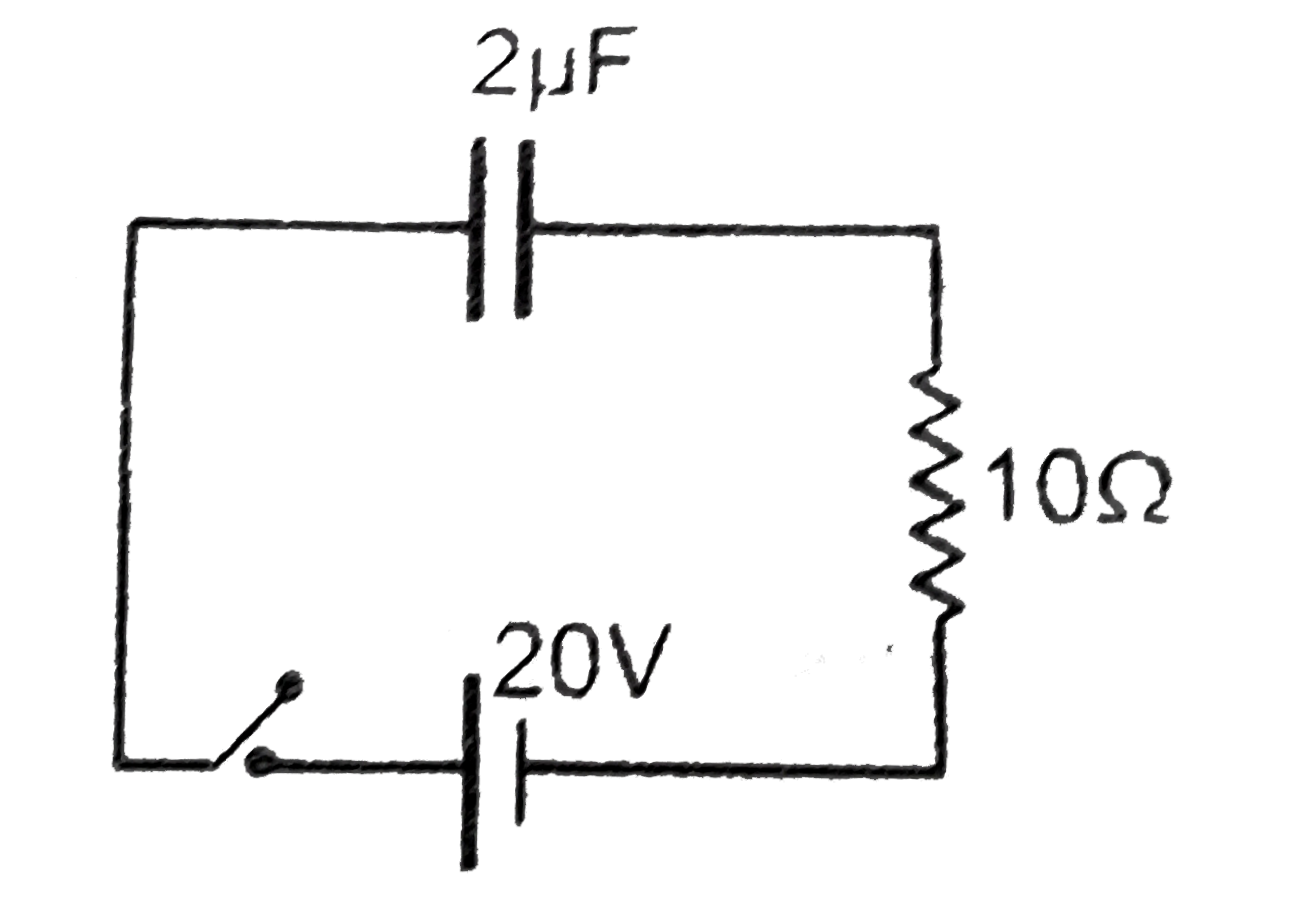
View Solution
