An L-C_R series circuit is joined to a source of alternating e.m.f. If R=9Ω,XL=28Ω,XC=16Ω, then the impedance of the circuit will be
10Ω
15Ω
20Ω
30Ω
The correct Answer is:B
Z=√R2+(XL−XC)2=√92+(28−16)2=15Ω.
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS EXERCISE - TEST YOUR GRASP - 1630videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS
- BOOK - MARVEL PUBLICATIONCHAPTER - ELASTICITYEXERCISE - Test Your Grasp - 515videos
ELASTICITY
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTRONS AND PHOTONS EXERCISE - TEST YOUR GRASP - 1715videos
ELECTRONS AND PHOTONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In series LCR circuit 3=ΩXL=8Ω,XC=4Ω, the impendance of the circuit is:
A3ΩB7ΩC5ΩD25Ω - Question 2 - Select One
An L-C-R series circuit , connected to a source E, is at resonance. Then,
Athe voltage across R is zeroBthe voltage across R equals applied voltageCthe volatage across C is zeroDthe voltage across C equals applied voltage - Question 3 - Select One
In an L-C-R series circuit R = 10Ω,XL=8Ωand XC=6Ωthe total impedance of the circuit is -
A10.2ΩB17.2ΩC10ΩDNone of the above
Consider the parallel resonant circuit shown in adjacent figure. One branch contains an inductor of inductance L and a small ohmic resistance R, whereas the other branch contains a capacitor of capacitance C. The circuit is fed by a source of alternating emfE=Eoejωt=Eosinωt
The impedance of inductor branch, Z(1)=R+jωL
The impendence of capacitor branch, Z(2) = (1//jomegaC)therefourNetimpedanceZofthetwoparal≤lbranchesisgivenby<br>(1)/(Z)=(1)/(Z_(1))+ (1)/)Z_(2)=(1)/(R+jomegaC<br>=(R-jomegaL)/(jomegaL)(R-jomegaL)+jomegaC=(R)/(R^(2)+omega^(2)+L^(2))+jomega[C-(L)/(R^(2)+omegaL^(2))]<br>Thecurrentflow∈g∈the∘uit<br>I=(E)/(Z)=(E)[(R)/(R^(2)+omega^(2)L^(2))+jomega(C-(L)/(R^(2)+omega^(2)L^(2)))]<br>Forresonance→our,thecurrentμstbe∈phasewiththeappliedemf.Forthis,thereactivecompo≠ntofcurrentshod––bezero,l.e.<br>omega[C-(L)/(R^(2)+omega^(2)L^(2))]=0<br>orC=(L)/(R^(2)+omega_(r)^(2)L^(2))(writ∈gomega_(r)foromegaatresonance)<br>Thisgivesresonantanga––requency<br>omega_(r)=sqrt((1)/(LC)-R^(2)/(L^(2))) At parallel circuit resonance, theimpendence is maximum and current is minimum. Parallel resonant circuit is sometimes called the anti-resonance in order to distinguish from series resonance
QFind the impedance of AC circuit at resonance shown in the adjacent figure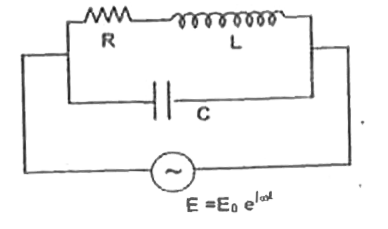
A coil of inductance 100 muH and 60 Omega effective resistance is connected in parallel with a condenser of 100 pF. The resonant circuit so formed is excited from an alternating current source. The frequency of the source is varied until the maximum impendence of the circuit is obtained. The frequency of the generator at which this occurs is approximatelyView SolutionConsider the parallel resonant circuit shown in adjacent figure. One branch contains an inductor of inductance L and a small ohmic resistance R, whereas the other branch contains a capacitor of capacitance C. The circuit is fed by a source of alternating emfE=Eoejωt=Eosinωt
The impedance of inductor branch, Z(1)=R+jωL
The impendence of capacitor branch, Z(2) = (1//jomegaC)therefourNetimpedanceZofthetwoparal≤lbranchesisgivenby<br>(1)/(Z)=(1)/(Z_(1))+ (1)/)Z_(2)=(1)/(R+jomegaC<br>=(R-jomegaL)/(jomegaL)(R-jomegaL)+jomegaC=(R)/(R^(2)+omega^(2)+L^(2))+jomega[C-(L)/(R^(2)+omegaL^(2))]<br>Thecurrentflow∈g∈the∘uit<br>I=(E)/(Z)=(E)[(R)/(R^(2)+omega^(2)L^(2))+jomega(C-(L)/(R^(2)+omega^(2)L^(2)))]<br>Forresonance→our,thecurrentμstbe∈phasewiththeappliedemf.Forthis,thereactivecompo≠ntofcurrentshod––bezero,l.e.<br>omega[C-(L)/(R^(2)+omega^(2)L^(2))]=0<br>orC=(L)/(R^(2)+omega_(r)^(2)L^(2))(writ∈gomega_(r)foromegaatresonance)<br>Thisgivesresonantanga––requency<br>omega_(r)=sqrt((1)/(LC)-R^(2)/(L^(2)))Atparal≤l∘uitresonance,theimpendenceismaxiμmandcurrentisminiμm.Paral≤lresonant∘uitissome×cal≤dtheanti−resonance∈order→dist∈guishomseriesresonance<br>QF∈dtheimpedanceofAC∘uitatresonanceshown∈theadjacentfigure<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/FIITJEE_PHY_MB_06_C03_E04_002_Q01.pngwh=80%mx-autosty≤=background:white;><br>Thereactanceofthe∘uit∈theadjacentfigureis20Ω.F∈dthevalueofI_(rms)
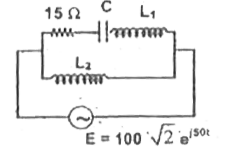 View Solution
View SolutionConsider the parallel resonant circuit shown in adjacent figure. One branch contains an inductor of inductance L and a small ohmic resistance R, whereas the other branch contains a capacitor of capacitance C. The circuit is fed by a source of alternating emfE=Eoejωt=Eosinωt
The impedance of inductor branch, Z(1)=R+jωL
The impendence of capacitor branch, Z(2) = (1//jomegaC)therefourNetimpedanceZofthetwoparal≤lbranchesisgivenby<br>(1)/(Z)=(1)/(Z_(1))+ (1)/)Z_(2)=(1)/(R+jomegaC<br>=(R-jomegaL)/(jomegaL)(R-jomegaL)+jomegaC=(R)/(R^(2)+omega^(2)+L^(2))+jomega[C-(L)/(R^(2)+omegaL^(2))]<br>Thecurrentflow∈g∈the∘uit<br>I=(E)/(Z)=(E)[(R)/(R^(2)+omega^(2)L^(2))+jomega(C-(L)/(R^(2)+omega^(2)L^(2)))]<br>Forresonance→our,thecurrentμstbe∈phasewiththeappliedemf.Forthis,thereactivecompo≠ntofcurrentshod––bezero,l.e.<br>omega[C-(L)/(R^(2)+omega^(2)L^(2))]=0<br>orC=(L)/(R^(2)+omega_(r)^(2)L^(2))(writ∈gomega_(r)foromegaatresonance)<br>Thisgivesresonantanga––requency<br>omega_(r)=sqrt((1)/(LC)-R^(2)/(L^(2))) At parallel circuit resonance, theimpendence is maximum and current is minimum. Parallel resonant circuit is sometimes called the anti-resonance in order to distinguish from series resonance
QFind the impedance of AC circuit at resonance shown in the adjacent figure

Find the impedance of AC circuit at resonance shown in the adjacent figure
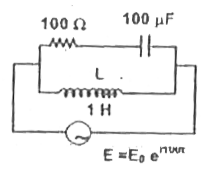 View Solution
View SolutionConsider the parallel resonant circuit shown in adjacent figure. One branch contains an inductor of inductance L and a small ohmic resistance R, whereas the other branch contains a capacitor of capacitance C. The circuit is fed by a source of alternating emfE=Eoejωt=Eosinωt
The impedance of inductor branch, Z(1)=R+jωL
The impendence of capacitor branch, Z(2) = (1//jomegaC)therefourNetimpedanceZofthetwoparal≤lbranchesisgivenby<br>(1)/(Z)=(1)/(Z_(1))+ (1)/)Z_(2)=(1)/(R+jomegaC<br>=(R-jomegaL)/(jomegaL)(R-jomegaL)+jomegaC=(R)/(R^(2)+omega^(2)+L^(2))+jomega[C-(L)/(R^(2)+omegaL^(2))]<br>Thecurrentflow∈g∈the∘uit<br>I=(E)/(Z)=(E)[(R)/(R^(2)+omega^(2)L^(2))+jomega(C-(L)/(R^(2)+omega^(2)L^(2)))]<br>Forresonance→our,thecurrentμstbe∈phasewiththeappliedemf.Forthis,thereactivecompo≠ntofcurrentshod––bezero,l.e.<br>omega[C-(L)/(R^(2)+omega^(2)L^(2))]=0<br>orC=(L)/(R^(2)+omega_(r)^(2)L^(2))(writ∈gomega_(r)foromegaatresonance)<br>Thisgivesresonantanga––requency<br>omega_(r)=sqrt((1)/(LC)-R^(2)/(L^(2))) At parallel circuit resonance, theimpendence is maximum and current is minimum. Parallel resonant circuit is sometimes called the anti-resonance in order to distinguish from series resonance
QFind the impedance of AC circuit at resonance shown in the adjacent figure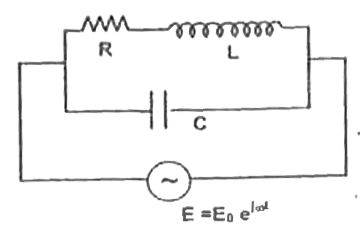
Which of the following graph shows correct relation beteen current I and frequency f in a parallel AC circuitView SolutionAn inductance of 0.4π henry and a resistace of 30Ω are joined in series. If an alternating e.m.f. of 200 V, 50 Hz is applied to their combination, then the impedance of the circuit will be
View Solution

