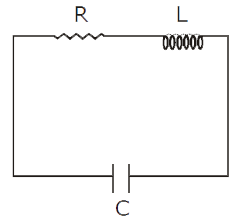
An LCR curcuit is equivalent to a damped pendulum. In an LCR circuit the capacitor is charged to (Q0) and then connected to the L ans R as shown below.
If a student plaots graphs of the square of maximum charge (Q2max) on the capacitor with time (t) for two different values L1andL2(L1>L2) of L then which of the following represents this graph correclty? (plots are schematic and not drawn to scale).
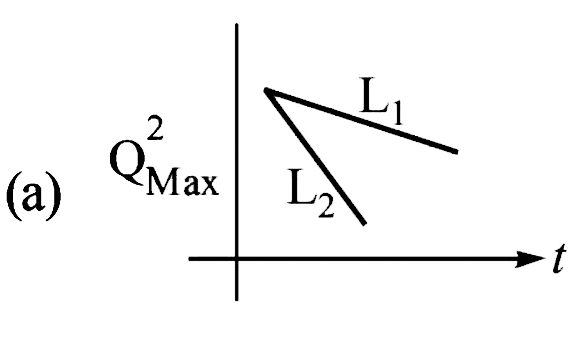
The correct Answer is:C
(c) From KVL at anytime t
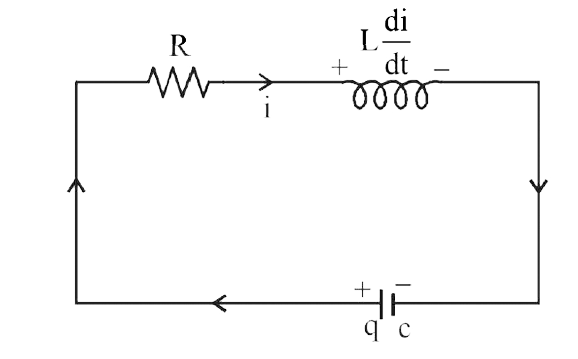
qc−iR−Ldidt)=0
i=−dqdt⇒qcR+ld2qdt2=0
(d^(2)q)/(dt^(2))+R/L (dq)/(dt)+(q)/(Lc)=0<br>Fromdampedharmonicoscilla→r,theamplitudeis<br>givenbyA=(A_(o)e-(dt)/(2m)<br>Doub≤d⇔erentialequation(d^(2)x)/(dt^(2))+b/m(dx)/(dt)+(k)/(m)x=0Q_(max)=(Q_o)e-(Rt)/(2L) implies Q_(o)^(2)e-(Rt)/(L)
Hence damping will be faster for leser inductance.
Topper's Solved these Questions
Similar Questions
The voltage-current graphs for two resistor of the same material and the same radius with lengths, L1andL2 are shown in fig 5.2. if L1>L2, state with reason which of these graphs represents voltage- current change of L1.
View SolutionIn the circuit shown in the figure, if both the lamps L1 and L2 are identical
View Solution
Knowledge Check
- Question 1 - Select One
An LCR circuit is equivalent to a damped pendulum In an LCR circuit the capacitor is charged to Q0 and then connected to the L and R as shown below : Thus potential energy stored in the capacitor and that in the inductor also oscillates between maximum value an zero with double the frequency.
If a student plots graphs of the square of maximum charge (Q2max) on the capacitor with time (t) for two different values L1andL2(L1>L2) of L then which of the following reprersent this graph correctly ? (Plots are shematic and not drawn to scale )A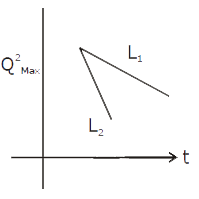
B
C
D
- Question 2 - Select One
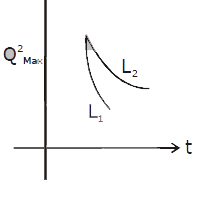
In an LC circuit the capacitor has maximum charge q0. The value of (dIdt)max is
Aq0LCBq0√LCCq0LC−1Dq0LC+1 - Question 3 - Select One
In LCR circuit, capacitor C is changed to 4C, then what should be the value of L to keep resonance frequency same
A2 LBL/2CL/4D4L
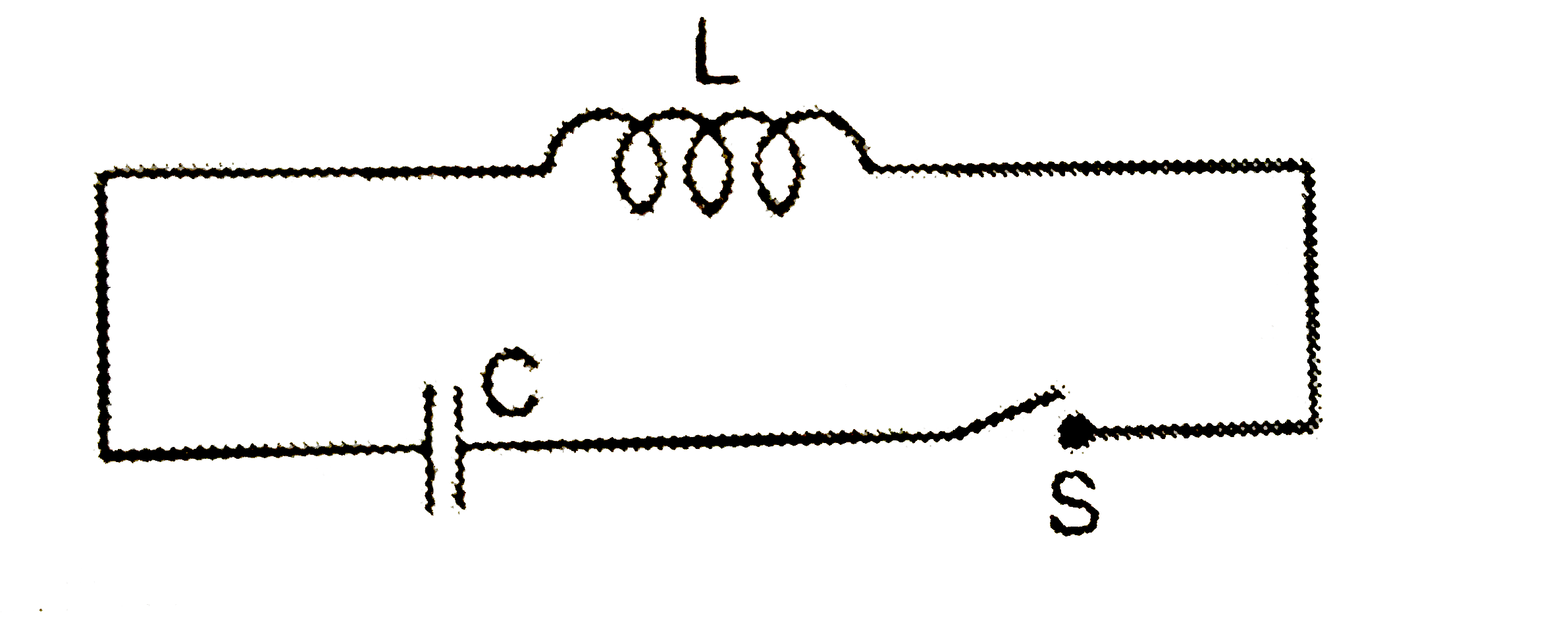
The capacitor of capacity C is given charge Q and then connected to the coil of inductance L by closing the switch S. The maximum current flowing in the circuit at any later time will beView SolutionThe current in an L - R circuit in a time t = 2L / R reduces to-
View SolutionWhen a capacitor is charged then
lc= conduction current ld = displacembet current)View SolutionA capacitor of capacitance C is given charge Q and then connected in parallel to a coil of inductance L. There is no resitance in the circuit. When the charge on the capacitor becomes zero, the current in the coil will be
View SolutionThe graph between L and T2 is
View Solution