An object 2.4 m in front of a lens forms a sharp image on a film 12 cm behind the lens. A glass plate 1 cm thick, of refractive index 1.50 is interposed between lens and film with its plane faces parallel to film. At what distance (from lens) should object shifted to be in sharp focus of film?
7.2 m
2.4 m
3.2 m
5.6 m
The correct Answer is:D
To solve the problem step by step, we will follow these procedures:
Step 1: Understand the given information
We have an object located 2.4 m (or 240 cm) in front of a lens, forming a sharp image 12 cm behind the lens. A glass plate of thickness 1 cm and refractive index 1.50 is placed between the lens and the film.
Step 2: Use the lens formula
The lens formula is given by:
1f=1v−1u
Where:
- f = focal length of the lens
- v = image distance from the lens
- u = object distance from the lens
Step 3: Substitute the known values into the lens formula
Given:
- v=12 cm (image distance, positive since it is on the opposite side of the object)
- u=−240 cm (object distance, negative as per sign convention)
Substituting these values into the lens formula:
1f=112−1−240
Calculating the right side:
1f=112+1240
Finding a common denominator (which is 240):
1f=20240+1240=21240
Thus, the focal length f is:
f=24021 cm≈11.43 cm
Step 4: Calculate the shift due to the glass plate
The shift S caused by the glass plate can be calculated using the formula:
S=t(1−1μ)
Where:
- t=1 cm (thickness of the glass plate)
- μ=1.50 (refractive index)
Substituting the values:
S=1(1−11.50)=1(1−23)=1(13)=13 cm
Step 5: Adjust the image distance
The new image distance v′ after placing the glass plate will be:
v′=v−S=12−13=363−13=353 cm
Step 6: Find the new object distance
Using the lens formula again with the new image distance v′:
1f=1v′−1u′
Rearranging gives:
1u′=1v′−1f
Substituting v′=353 cm and f=24021 cm:
1u′=335−21240
Finding a common denominator (which is 240):
1u′=3⋅24035⋅240−21⋅35240⋅35
Calculating:
1u′=7208400−7358400=−158400
Thus:
u′=−840015=−560 cm
Step 7: Conclusion
The object should be shifted to a distance of approximately 5.6 cm from the lens to be in sharp focus on the film.
We have an object located 2.4 m (or 240 cm) in front of a lens, forming a sharp image 12 cm behind the lens. A glass plate of thickness 1 cm and refractive index 1.50 is placed between the lens and the film.
The lens formula is given by:
1f=1v−1u
Where:
- f = focal length of the lens
- v = image distance from the lens
- u = object distance from the lens
Given:
- v=12 cm (image distance, positive since it is on the opposite side of the object)
- u=−240 cm (object distance, negative as per sign convention)
1f=112−1−240
Calculating the right side:
1f=112+1240
Finding a common denominator (which is 240):
1f=20240+1240=21240
Thus, the focal length f is:
f=24021 cm≈11.43 cm
The shift S caused by the glass plate can be calculated using the formula:
S=t(1−1μ)
Where:
- t=1 cm (thickness of the glass plate)
- μ=1.50 (refractive index)
S=1(1−11.50)=1(1−23)=1(13)=13 cm
The new image distance v′ after placing the glass plate will be:
v′=v−S=12−13=363−13=353 cm
Using the lens formula again with the new image distance v′:
1f=1v′−1u′
Rearranging gives:
1u′=1v′−1f
Substituting v′=353 cm and f=24021 cm:
1u′=335−21240
Finding a common denominator (which is 240):
1u′=3⋅24035⋅240−21⋅35240⋅35
Calculating:
1u′=7208400−7358400=−158400
Thus:
u′=−840015=−560 cm
The object should be shifted to a distance of approximately 5.6 cm from the lens to be in sharp focus on the film.
Topper's Solved these Questions
Similar Questions
An object 240 cm in front of a lens forms a sharp image on a screen 12 cm behind the lens. A glass slab 1 cm thick, having refractive index 1.50 is placed between the lens and the screen with its refracting faces perpendicular to the principal axis of the lens.
(a) By how much distance the object must be moved so as to again cast a sharp image on the screen?
(b) Another identical glass slab is interposed between the object and the lens. How much further the object shall be moved so as to form a sharp image on the screen.
View SolutionAn object is placed 12cm in front of a lens to form an image on a screen. The size of the image is twice that of the object. What is the distance between the object and the image?
View Solution
Knowledge Check
An object placed 10cm in front of a lens has an image 20cm behind the lens. What is the power of the lens( in diopters ) ?
A1.5B3.0C−15.0D+15.0A point object is placed at a distance of 25 cm from a convex lens of focal length 20cm. If a glass slab of thickness t and refractive index 1.5 is inserted between the lens and the object, the image is formed at infinity. The thickness t is
A10cmB5cmC20cmD15cmA point object is placed at a diatance of 25 cm from a convex lens of focal length 20 cm. If a glass slab of thickness t and refractive index 1.5 is inserted between the lens and the object, the image is formed at infinity. The thickness t is
A10 cmB5 cmC20 cmD15 cm
A point object is placed at a distance of25cmfrom a convex lens of focal length 20cm.If a glass slab of thicknesstand refractive index 1.5is inserted between the lens and object.The image is formed at infinity .Find the thickness?
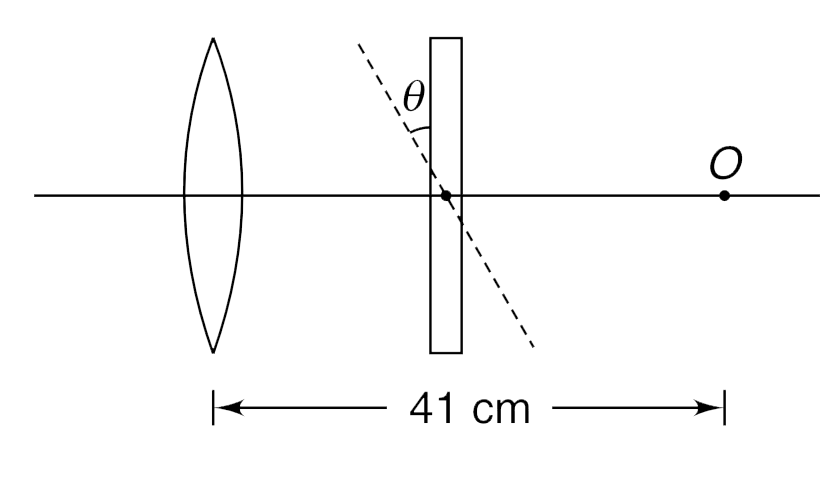
View SolutionA point object O is placed at a distance of 41 cm from a convex lens of focal length f=20 cm on its principal axis. A glass slab of thickness 3 cm and refractive index μ=1.5 is placed between the lens and the object with its faces perpendicular to the principal axis of the lens. Image of the object is formed at point I1. Now the glass slab is tilted by an angle of θ=1° (as shown in the Figure) and the final image is formed at I2. Calculate the distance between points I1 and I2. Consider only paraxial rays for the lens and near normal incidence for the glass slab.
View SolutionA point object is placed at a distance of 25cm from a convex lens. Its focal length is 22cm. A glass slab of refractive index 1.5 is inserted between the lens and the object, then the image is formed at infinity. Find the thickness of the glass slab (in cm).
View SolutionA point object is placed at a distance 25cm from a convex lens of focal length 20cm. If a glass slab of thickness t annd refractive index 1.5 is inserted between the lens and object, image is formed at . Thickness t is found to be K times of 5cm. Fink K.
View SolutionFocal length of an equiconvex lens is 20 cm. The refractive index of material of the lens is 1.5. Now one of the curved surface is silvered. At what distance from the lens an object is to be placed, so that image coincides with the object ?
View Solution
