An object approaches a convergent lens from the left of the lens with a uniform speed 5m/s and stops at the focus. The image.
moves away from the lens with an uniform speed 5ms−1
moves away from the lens with an uniform acceleration
moves away from the lens with a non-uniform acceleration
moves towards the lens with a non -uniform acceleration.
The correct Answer is:C
To solve the problem of how the image behaves as an object approaches a convergent lens with a uniform speed, we can follow these steps:
Step 1: Understand the Lens Formula
The lens formula relates the object distance (u), the image distance (v), and the focal length (f) of the lens:
1f=1v−1u
Where:
- u is the object distance (negative in lens convention),
- v is the image distance (positive for real images),
- f is the focal length (positive for converging lenses).
Step 2: Define the Initial Conditions
Assume the focal length f of the lens is given (for example, 20 cm). The object starts at a distance greater than the focal length and approaches the lens at a speed of 5m/s.
Step 3: Calculate Image Distance at Various Object Distances
As the object approaches the lens, we can calculate the image distance v for several values of u (object distance). For example:
- If u=−50cm:
120=1v−1−50⟹v=33.3cm
- If u=−45cm:
120=1v−1−45⟹v=36cm
- If u=−40cm:
120=1v−1−40⟹v=40cm
Step 4: Analyze the Variation of Image Distance
As the object moves closer to the lens, we observe that the image distance v changes non-linearly. The image distance increases at a varying rate as the object approaches the focus.
Step 5: Determine the Nature of Image Motion
Since the object is moving towards the lens at a constant speed, the change in image distance v is not uniform. The image distance increases with a non-uniform acceleration because the rate of change of v with respect to u is not constant.
Conclusion
Thus, the image moves away from the lens with a non-uniform acceleration as the object approaches the focus.
The lens formula relates the object distance (u), the image distance (v), and the focal length (f) of the lens:
1f=1v−1u
Where:
- u is the object distance (negative in lens convention),
- v is the image distance (positive for real images),
- f is the focal length (positive for converging lenses).
Assume the focal length f of the lens is given (for example, 20 cm). The object starts at a distance greater than the focal length and approaches the lens at a speed of 5m/s.
As the object approaches the lens, we can calculate the image distance v for several values of u (object distance). For example:
- If u=−50cm:
120=1v−1−50⟹v=33.3cm
- If u=−45cm:
120=1v−1−45⟹v=36cm
- If u=−40cm:
120=1v−1−40⟹v=40cm
As the object moves closer to the lens, we observe that the image distance v changes non-linearly. The image distance increases at a varying rate as the object approaches the focus.
Since the object is moving towards the lens at a constant speed, the change in image distance v is not uniform. The image distance increases with a non-uniform acceleration because the rate of change of v with respect to u is not constant.
Thus, the image moves away from the lens with a non-uniform acceleration as the object approaches the focus.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSERTION AND REASON
15 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - MULTIPLE CHOICE QUESTIONS
100 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT Exemplar
11 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A point object O approaches a biconvex lens of focal length 40 cm along its optic axis with a speed of 10 m/s while the later receeds away from the former with a speed of 4 cm/s. Find the speed and direction of motion of the image when the object is at a distance of 60 cm from the lens.

View SolutionAn object is approaching a convex lens of focal length 0.3m with a speed of 0.01ms−1. Find the magnitudes of the ratio of change of position and lateral magnification of image when the object is at a distance of 0.4m from the lens
View SolutionAn object is placed at the focus of an equiconvex lens. Match the following

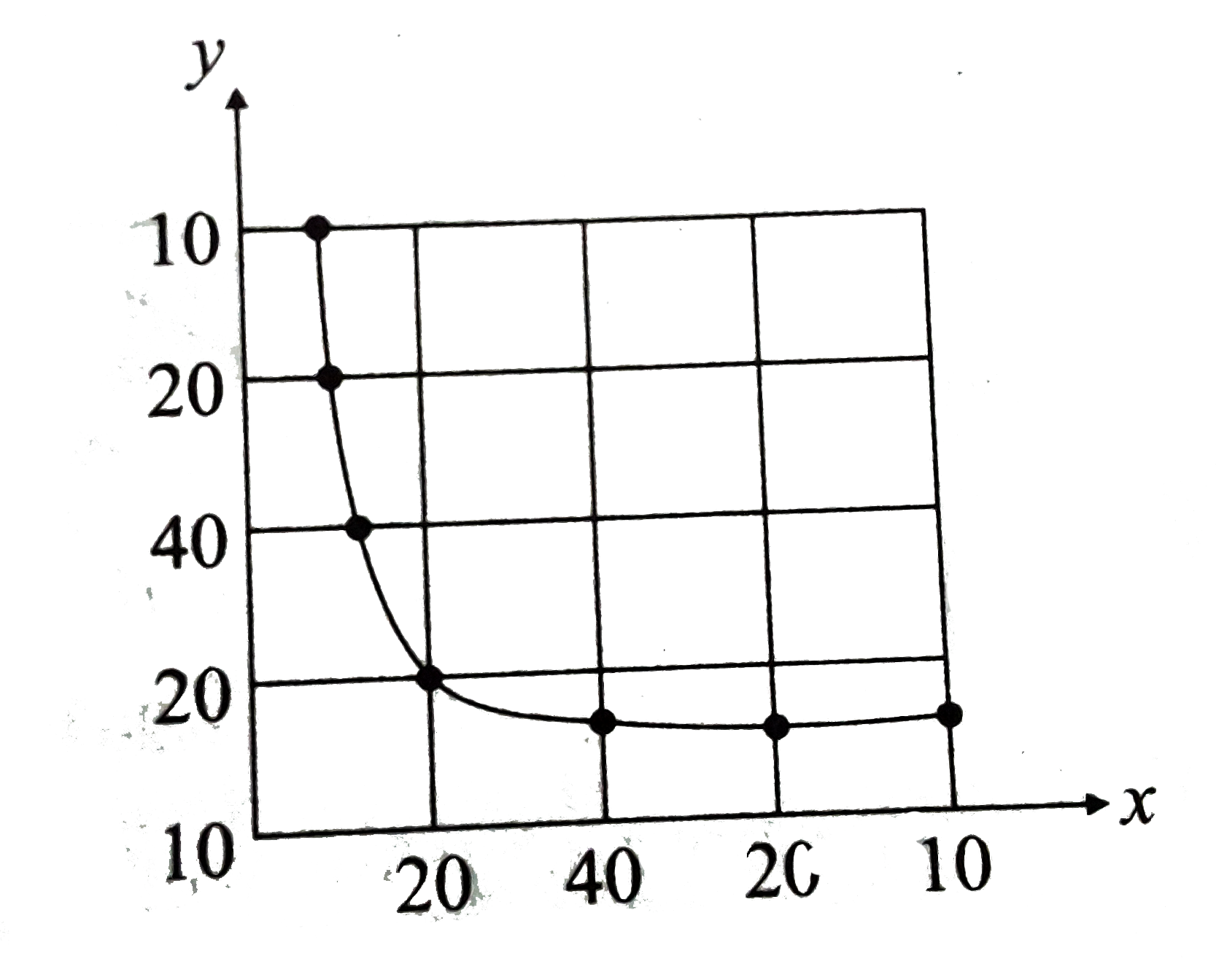
View SolutionA lens forms a real image of an object. The distance from the object to the lens is x cm and that from the lens to the image is y cm. The graph shows the variation of y with x.
It can be deduced that the lens is
View SolutionAn object is at a distance of 20 m form a convex lens of focal length 0.3m The lens forms an image of the object moves away form the lens at a speed of 5m/s the speed and direction of the image will be :
View SolutionFigure shows a point object and a converging lens. Find the final image formed.

View SolutionAn object is moving towards a converging lens on its axis. The image is also found to be moving towards the lens. Then, the object distance u must satisfy
View SolutionAn object is placed in front of a lens between its optical centre and the focus and forms a virtual, erect and diminished image.
Name the lens which formed this image.
View SolutionA lens produces a virtual image between the object and the lens.
Name the lens.
View SolutionAn object is placed in front of a concave lens. A virtual image of the object is formed on the same side of the lens as the object but is closer to the lens. Will rays form this image refract once again at the lens to form a second image?
View Solution
