An object has velocity →v1 w.r.t. ground. An observer moving with constant velocity →v0 w.r.t. ground measures the velocity of the object as →v2. The magnitudes of three velocities are related by
v0≥v1+v2
v1≤v2+v0
v2≥v1+v0
All of the above
The correct Answer is:B
To solve the problem, we need to relate the velocities of the object, the observer, and the object as measured by the observer using vector addition and the triangle inequality.
1. Define the Velocities:
- Let →v1 be the velocity of the object with respect to the ground.
- Let →v0 be the velocity of the observer with respect to the ground.
- Let →v2 be the velocity of the object as measured by the observer.
2. Relative Velocity Concept:
- The velocity of the object with respect to the observer can be expressed as:
→v2=→v1−→v0
- This equation shows that to find the velocity of the object relative to the observer, we subtract the observer's velocity from the object's velocity.
3. Magnitude Relation:
- The magnitudes of these velocities can be related using the triangle inequality. According to the triangle inequality, for any three vectors →A,→B,→C:
|→A+→B|≤|→C|
- In our case, we can rearrange the equation:
|→v1|=|→v2+→v0|
4. Applying Triangle Inequality:
- From the triangle inequality, we know:
|→v2|+|→v0|≥|→v1|
- This means that the sum of the magnitudes of the velocities |→v2| and |→v0| is greater than or equal to the magnitude of |→v1|.
5. Conclusion:
- Therefore, the relationship between the magnitudes of the three velocities is:
|→v2|+|→v0|≥|→v1|
Final Answer:
The magnitudes of the three velocities are related by:
|→v2|+|→v0|≥|→v1|
- Let →v1 be the velocity of the object with respect to the ground.
- Let →v0 be the velocity of the observer with respect to the ground.
- Let →v2 be the velocity of the object as measured by the observer.
- The velocity of the object with respect to the observer can be expressed as:
→v2=→v1−→v0
- This equation shows that to find the velocity of the object relative to the observer, we subtract the observer's velocity from the object's velocity.
- The magnitudes of these velocities can be related using the triangle inequality. According to the triangle inequality, for any three vectors →A,→B,→C:
|→A+→B|≤|→C|
- In our case, we can rearrange the equation:
|→v1|=|→v2+→v0|
- From the triangle inequality, we know:
|→v2|+|→v0|≥|→v1|
- This means that the sum of the magnitudes of the velocities |→v2| and |→v0| is greater than or equal to the magnitude of |→v1|.
- Therefore, the relationship between the magnitudes of the three velocities is:
|→v2|+|→v0|≥|→v1|
The magnitudes of the three velocities are related by:
|→v2|+|→v0|≥|→v1|
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Multiple Correct Answer Type
26 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Select the odd one w.r.t. ground tissue system is
View SolutionA person crossing a road with a certain velocity due north sees a car moving towards east The relative velocity of the car w.r.t the person is √2 times that fo the velocity of the persons. The angle made by the relative velocity with the east is
View Solutionf A and B persons are moving with VAandVB. velocities in opposite directions. Magnitude of relative velocity of B w.r.t. A is x and magni-tude of relative velocity of A w.r.t B is y. Then
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
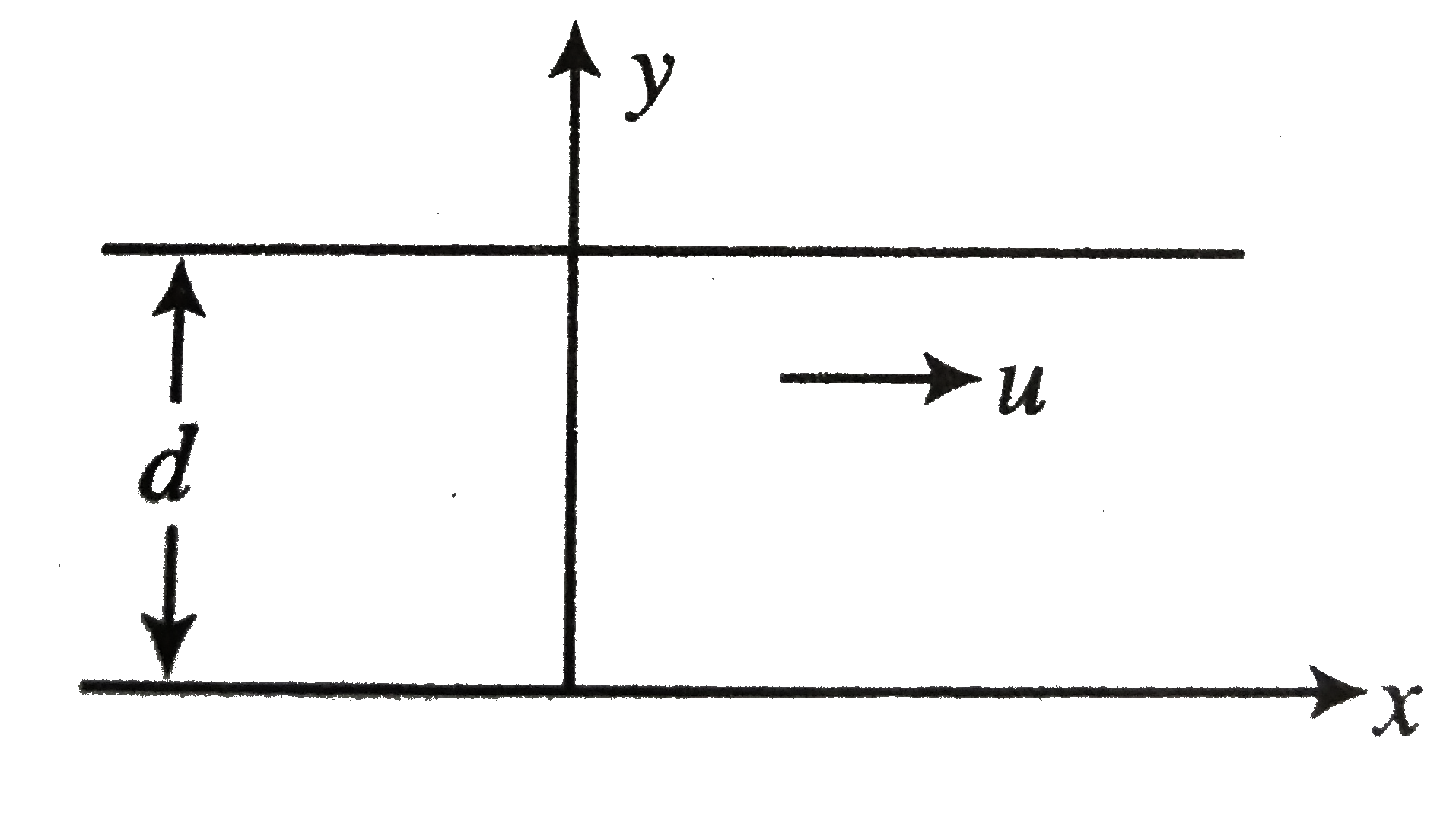
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units. Find time taken by him to across the river.
View SolutionTwo objects A and B are moving in opposite directions with velocities vAandvB respectively, the magnitude of relative velocity of A w.r.t. B is
View SolutionAn uncharged particle is moving with a velocity of →v in non - uniform magnetic field as shown

Velocity →v would be
View SolutionThe velocity varies with time as →v=aˆi+btˆj , where a and b are positive constants. The magnitude of instantaneous velocity and acceleration would be
View SolutionA particle moving with velocity →V is acted by the three forces shown by the vector triangle PQR. The velocity of the particle will :

View Solution
