An object is placed 1m in front of the curved surface of a plano-convex lens whose plane surface is silvered. A real image is formed in front of the lens at a distance of 120cm. Then, the focal length of the lens is
100cm
120cm
109.1cm
110.0cm
The correct Answer is:c.
To solve the problem, we need to find the focal length of a plano-convex lens with its plane surface silvered. The object is placed 1 meter (100 cm) in front of the lens, and a real image is formed at a distance of 120 cm in front of the lens.
1. Identify the given values:
- Object distance (u) = -100 cm (negative because it is in front of the lens)
- Image distance (v) = -120 cm (negative because the image is formed in front of the lens)
- The lens is plano-convex with its plane surface silvered.
2. Understand the behavior of the lens:
- The plano-convex lens will refract the light at the curved surface and reflect it at the silvered plane surface.
- The image formed by the lens will act as a virtual object for the plane mirror (silvered surface).
3. Apply the lens formula for the first surface (curved surface):
1f=1v1−1u
Here, v1 is the image distance formed by the lens before it reflects off the silvered surface. We will denote the focal length of the lens as f.
4. Rearranging the lens formula:
1v1=1f+1100
This gives us our first equation (Equation 1).
5. Consider the second surface (silvered plane surface):
- The image formed by the lens acts as a virtual object for the silvered surface. The distance of this virtual object from the silvered surface is v1.
- For the silvered surface, the object distance is equal to the image distance (as per the mirror formula):
v1=−v1
6. Apply the lens formula for the second surface:
1f=1120−1v1
Rearranging gives us:
1v1=1120−1f
This gives us our second equation (Equation 2).
7. Substitute Equation 1 into Equation 2:
From Equation 1, we have:
1v1=1f+1100
Substitute this into Equation 2:
1f+1100=1120−1f
8. Combine and solve for f:
2⋅1f=1120−1100
Finding a common denominator (600):
2⋅1f=5−6600=−1600
Thus,
1f=−11200
Therefore,
f=−1200 cm
9. Final Calculation:
Since the focal length is positive for a plano-convex lens, we take the absolute value:
f=1200 cm
Conclusion:
The focal length of the plano-convex lens is 120 cm.
- Object distance (u) = -100 cm (negative because it is in front of the lens)
- Image distance (v) = -120 cm (negative because the image is formed in front of the lens)
- The lens is plano-convex with its plane surface silvered.
- The plano-convex lens will refract the light at the curved surface and reflect it at the silvered plane surface.
- The image formed by the lens will act as a virtual object for the plane mirror (silvered surface).
1f=1v1−1u
Here, v1 is the image distance formed by the lens before it reflects off the silvered surface. We will denote the focal length of the lens as f.
1v1=1f+1100
This gives us our first equation (Equation 1).
- The image formed by the lens acts as a virtual object for the silvered surface. The distance of this virtual object from the silvered surface is v1.
- For the silvered surface, the object distance is equal to the image distance (as per the mirror formula):
v1=−v1
1f=1120−1v1
Rearranging gives us:
1v1=1120−1f
This gives us our second equation (Equation 2).
From Equation 1, we have:
1v1=1f+1100
Substitute this into Equation 2:
1f+1100=1120−1f
2⋅1f=1120−1100
Finding a common denominator (600):
2⋅1f=5−6600=−1600
Thus,
1f=−11200
Therefore,
f=−1200 cm
Since the focal length is positive for a plano-convex lens, we take the absolute value:
f=1200 cm
The focal length of the plano-convex lens is 120 cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
Knowledge Check
The radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
Aact as a convex lens only for the objects that lie on its curved side.Bact as a concave lens for the objects that lie on its curved side.Cact as a convex lens irrespective of the side on which the object lies.Dact as a concave lens irrespective of side on which the object lies.
The flat face of a plano-convex lens of focal length 10 cm is silvered. A point source placed 30 cm in front of the curved surface will produce a
View SolutionThe plane surface of a plano-convex lens of focal length 60 cm is silvered. A point object is placed at a distance 20 cm from the lens. Find the position and nature of the final image formed.
View SolutionA plano-convex lens P and a concavo-convex lens Q are in contact as shown in figure. The refractive index o fthe material of the lens P and Q is 1.8and1.2 respectively. The radius of curvature of the concave surface of the lens Q is double the radius of curvature of the convex surface. The convex surface of Q is silvered.

An object is placed on the placed on the principal axis at a distance 10cm form the plane surface. The image is formed at a distance 40cm from the plane surfaces on the same side. The focal length of the system is
View SolutionA point object is placed in front of a silvered plano convex lens of refractive index n radius of curvature R, so that its image is formed on itself. Then the object distance is equal to

View SolutionA point object is placed at a distance of 20cm from a thin plano-convex lens of focal length 15cm(μ=1.5). The curved surface is silvered. The image will form at
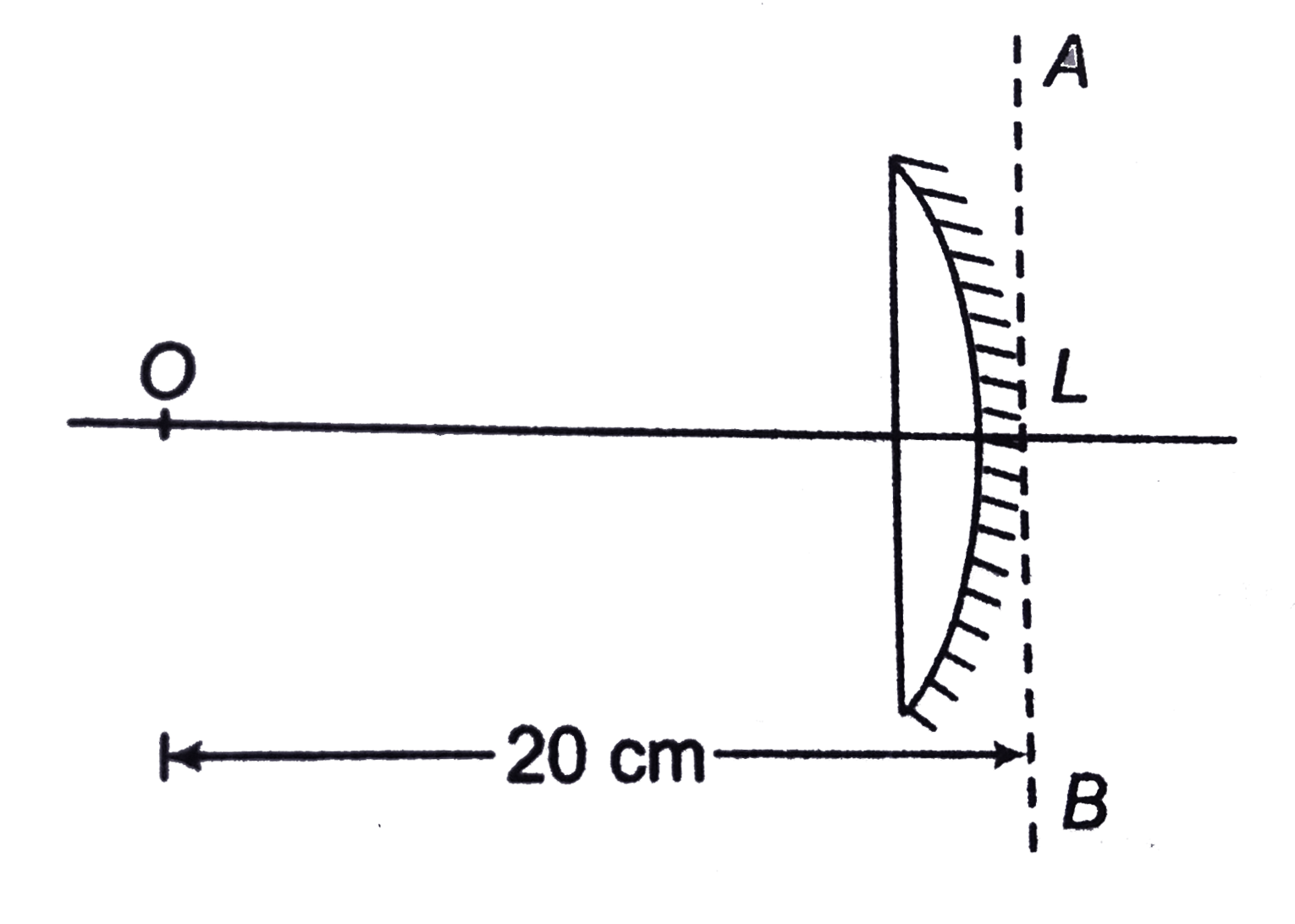
View SolutionA point object is placed at a distance of 20cm from a thin plano-convex lens of focal length 15cm(μ=1.5). The curved surface is silvered. The image will form at

View SolutionThe radius of curvature of curved surface of a thin plano-convex lens is 10cm and the refractive index is 1.5. If the plano surface is silvered, then the focal length will be.
View Solution
