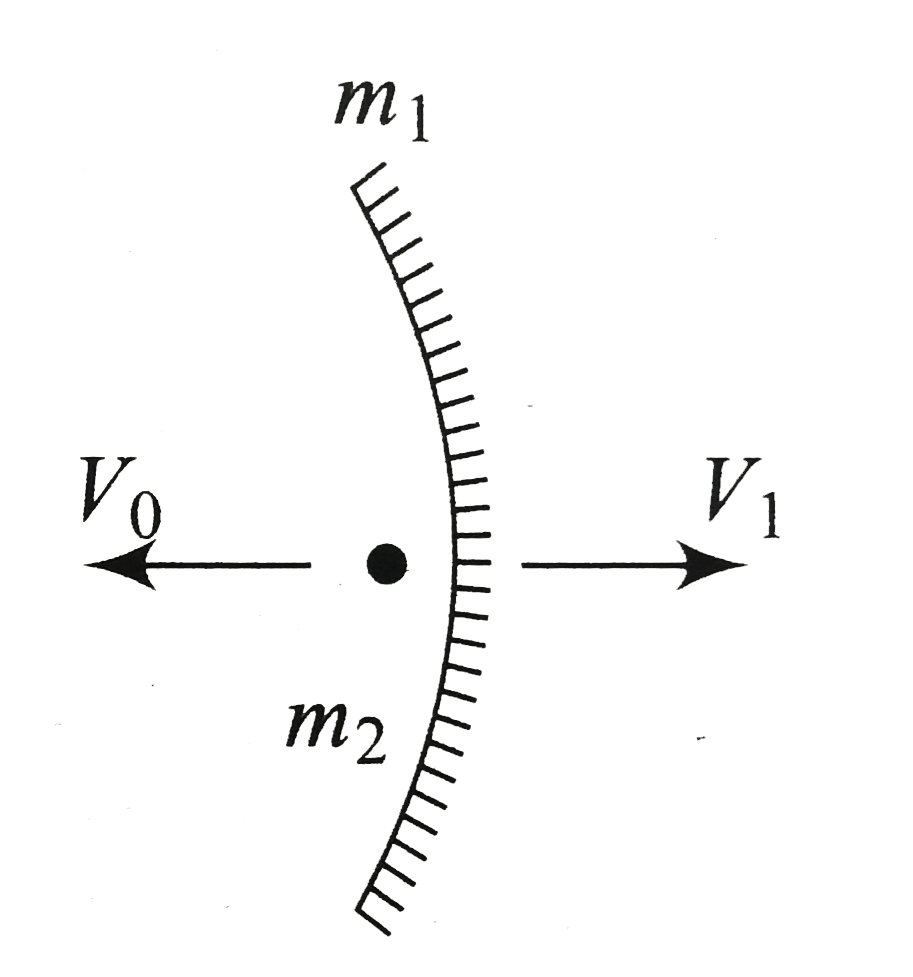
A gun of mass M fires a bullet of mass m with a horizontal speed V. The gun is fitted with a concave mirror of focal length f facing towards the receding bullet. Find the speed of separation of the bullet and the image just after the gun was fired.

A

$(1 + \frac{m_{2}}{m_{1}}) v_{0}$

B

$2 (1 - \frac{m_{2}}{m_{1}}) v_{0}$

C

$2 (1 + \frac{2 m_{2}}{m_{1}}) v_{0}$

D

$2 (1 + \frac{m_{2}}{m_{1}}) v_{0}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Let $v_{1}$ be the speed of gun (or mirror) just after the firing of bullet. From conservation of linear momentum,
$m_{2} v_{0} = m_{1} v_{1}$
$v_{1} = \frac{m_{2} v_{0}}{m_{1}}$ (i)
Now rate at which distance between mirror and bullet is increasing,
$\frac{d u}{d t} = v_{1} + v_{0}$ (ii)
$\frac{d v}{d t} = (\frac{v^{2}}{u^{2}}) \frac{d u}{d v}$
Here, $\frac{v^{2}}{u^{2}} = m^{2} = 1$
(as at the itme of firing, the bullet is at pole).
$\frac{d v}{d t} = \frac{d u}{d t} = v_{1} + v_{0}$ (iii)
Here, $d v / d t$ is the rate at which distance between image (of bullet) and mirror is increasing . So, if $v_{2}$ is the absolute velocity of image (towards right), then
$v_{2} - v_{1} = \frac{d v}{d t} = v_{1} + v_{0}$
or $v_{2} = 2 v_{1} + v_{0}$ (iv)
Therefore, speed of separation of the bullet and the image will be
$v_{r} = v_{2} + v_{0} = 2 v_{1} + v_{0} + v_{0}$
$v_{r} = 2 (v_{1} + v_{0})$
Substituting value of $v_{1}$ from Eq. (i), we have
$v_{r} = 2 (1 + \frac{m_{2}}{m_{1}}) v_{0}$

Updated on:21/07/2023

|

Class 12 PHYSICS RAY OPTICS AND OPTICAL INSTRUMENTS

Topper's Solved these Questions

Similar Questions

Knowledge Check

A machine gun fires n bullets per second and the mass of each bullet is m. If v is the speed of each bullet, then the force exerted on the machine gun is
Am n g
Bm n v
Cm n v g
D(m n v )/g

CENGAGE PHYSICS ENGLISH-GEOMETRICAL OPTICS-Single Correct

Home
Ask Doubt
Profile