An object is placed at a distance of 15cm from a convex lenx of focal length 10cm. On the other side of the lens, a convex mirror is placed at its focus such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
20 cm
10 cm
15 cm
30 cm
The correct Answer is:B
To solve the problem step by step, we will use the lens formula and the properties of mirrors.
Step 1: Identify the given values
- Object distance from the convex lens (U) = -15 cm (negative because it is on the same side as the incoming light)
- Focal length of the convex lens (F) = +10 cm (positive for a convex lens)
Step 2: Use the lens formula to find the image distance (V)
The lens formula is given by:
1V−1U=1F
Rearranging the formula gives:
1V=1F+1U
Substituting the known values:
1V=110+1−15
Finding a common denominator (30):
1V=330−230=130
Thus,
V=30 cm
Step 3: Determine the position of the image formed by the lens
The image formed by the lens is at a distance of 30 cm on the opposite side of the lens.
Step 4: Analyze the convex mirror
The convex mirror is placed at the focus of the lens, which is 10 cm from the lens. Since the image formed by the lens is at 30 cm, the distance from the lens to the mirror is:
30 cm−10 cm=20 cm
This means that the image formed by the lens is 20 cm away from the convex mirror.
Step 5: Use the mirror formula to find the focal length of the convex mirror
For a convex mirror, the focal length (f) is related to the radius of curvature (R) by:
f=R2
Since the image coincides with the object, the distance from the convex mirror to the image is equal to the radius of curvature. Therefore, the radius of curvature (R) is 20 cm.
Step 6: Calculate the focal length of the convex mirror
Substituting R into the focal length formula:
f=20 cm2=10 cm
Conclusion
The focal length of the convex mirror is 10 cm.
- Object distance from the convex lens (U) = -15 cm (negative because it is on the same side as the incoming light)
- Focal length of the convex lens (F) = +10 cm (positive for a convex lens)
The lens formula is given by:
1V−1U=1F
Rearranging the formula gives:
1V=1F+1U
Substituting the known values:
1V=110+1−15
Finding a common denominator (30):
1V=330−230=130
Thus,
V=30 cm
The image formed by the lens is at a distance of 30 cm on the opposite side of the lens.
The convex mirror is placed at the focus of the lens, which is 10 cm from the lens. Since the image formed by the lens is at 30 cm, the distance from the lens to the mirror is:
30 cm−10 cm=20 cm
This means that the image formed by the lens is 20 cm away from the convex mirror.
For a convex mirror, the focal length (f) is related to the radius of curvature (R) by:
f=R2
Since the image coincides with the object, the distance from the convex mirror to the image is equal to the radius of curvature. Therefore, the radius of curvature (R) is 20 cm.
Substituting R into the focal length formula:
f=20 cm2=10 cm
The focal length of the convex mirror is 10 cm.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - C. comprehension type question
14 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
A point object is placed at a distance of 12cm from a convex lens of focal length 10cm. On the other side of the lens, a convex mirror is placed at a distance of 10cm from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
nature of the image
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View SolutionFocal length of a convex mirror is 10 cm
View SolutionA point object O is placed at a distance of 15 cm from a convex lens L of focal length 10 cm as shown in figure below. On the other side of the lens, a convex mirror M is placed such that its distance from the lens is equal to the focal length of the lens. The final image formed by this combination is observed to coincide with the object 0. Find the focal length of the convex mirror.
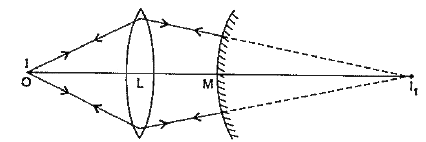
View SolutionAn object is placed at a distance 24 cm in front of a convex lens of focal length 8 cm.
Calculate the distance of the image from the lens.
View SolutionAn object is placed at 20 cm from a convex mirror of focal length 20 cm. The distance of the image from the pole of the mirror is
View SolutionAn object is placed at a distance 20 cm from the pole of a convex mirror of focal length 20 cm. The image is produced at
View SolutionAn object is placed at 20 cm from a convex mirror of focal length 10 cm. The image formed by a mirror is
View SolutionA point object is placed at distance of 30 cm in front of a convex mirror of Focal length 30 cm. The image will form at
View Solution
