An object is thrown towards the tower which is at a horizontal distance of 50 m with an initial velocity of 10ms−1 and making an angle 30∘ with the horizontal. The object hits the tower at certain height. The height from the bottom of the tower, where the object hits the tower is (Take, g=10ms−2)
50√3[1−10√3]m
503[1−10√3]m
100√3[1−10√3]m
1003[1−10√3]m
The correct Answer is:A
Consider the diagram.
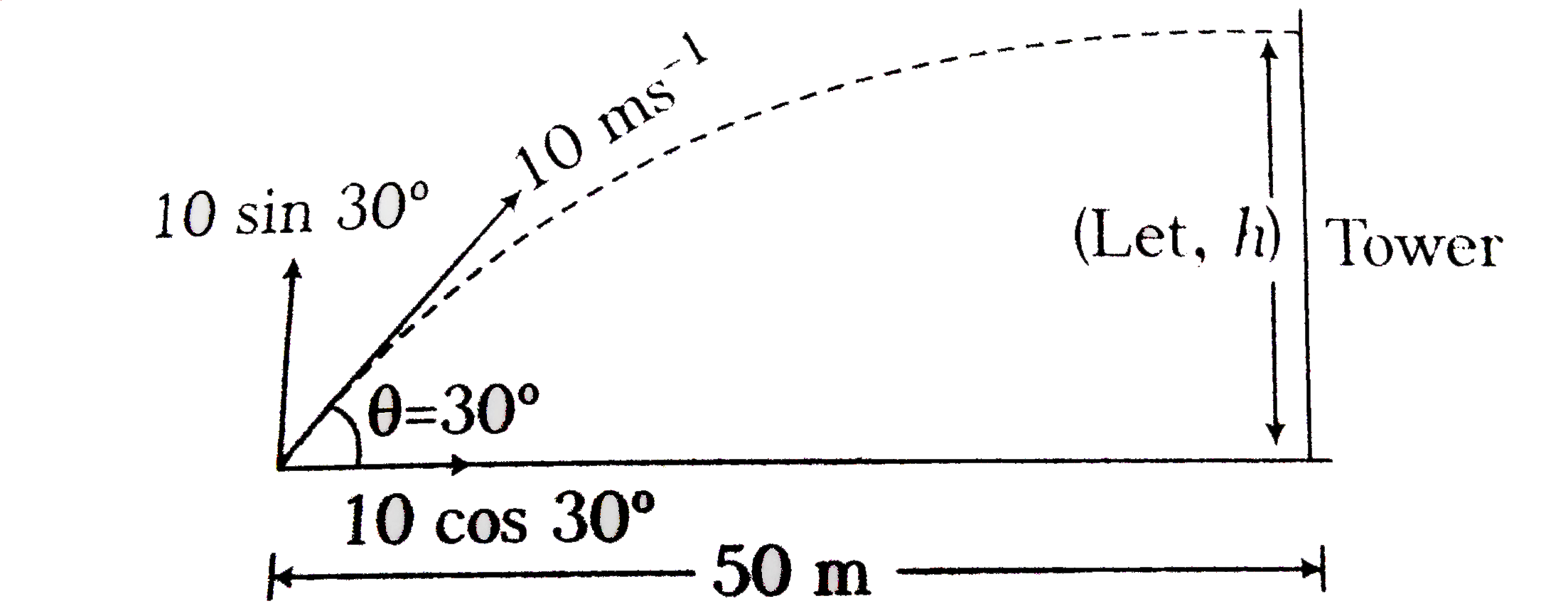
For horizontal motion,
50=10cos30∘×t
⇒t=5cos30∘=5√32=10√3
For vertical motion,
h=10sin30∘×10√3−12×10×(10√3)2
=10×12×10√3−100√35√3=100√3(12−5√3)
=50√3[1−10√3]m
Topper's Solved these Questions
Similar Questions
A ball is thrown from the top of a tower with an initial velocity of 10 m//s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
View SolutionA ball is thrown from the top of a tower of 61m high with a velocity 24.4ms−1 at an elevation of 30∘ above the horizontal. What is the distance from the foot of the tower to the point where the ball hits the ground?
View Solution
Knowledge Check
A ball is thrown from the top of tower with an initial velocity of 10ms−1 at an angle of 30∘ with the horizontal. If it hits the ground of a distance of 17.3m from the back of the tower, the height of the tower is (Takeg=10ms−2)
A5mB20mC15mD10mA stone is thrown from the top of a tower of height 50m with a velocity of 30ms−1 at an angle of 30∘ above the horizontal.Find the time during which the stone will be in air
A2secB3secC4secD5secA ball is projected upwards from the top of a tower with a velocity 50ms−1 making an angle 30∘ with the horizontal. The height of tower is 70m. After how many seconds from the instant of throwing, will the ball reach the ground. (g=10ms−2)
A2 sB5 sC7 sD9 s
A ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
View SolutionA stone is thrown up from the top of a tower 20,m with a velocity of 24m/s a tan elevation of 30∘ above the horizontal. Find the horizontal distance from the foot of the tower to the point at which the stone hits the ground. Take g=10m/s2
View SolutionA ball is thrown with velocity 40m/s at angle 30∘ with horizontal from the top of a tower of height 60m. At what horizontal distance from the foot of tower, the ball will strike the gorund ?
View SolutionA stone is thrown from the top of a tower of height 50 m with a velocity of 30 m per second at an angle of 30∘ above the horizontal. Find (a) the time during which the stone will be in air, (b) the distance from the tower base to where the stone will hit the ground, (c) the speed with which the stone will hit the ground, (d) the angle formed by the trajectory of the stone with the horizontal at the point of hit.
View SolutionThe angle of elevation of the top of a tower at a horizontal distance equal to the height of the tower from the base of the tower is
View Solution
