An object of mass m slides down a hill of height h of arbitrary shape

An object of mass $m$ slides down a hill of arbitrary shape and after travelling a certain horizontal path stops because of friction. The total vertical height descended is $h$ . The friction coefficient is different for different segments for the entire path but is independent of the velocity and direction of motion. The work that a tangerial force must perform to return the object to its initial position along the same path is

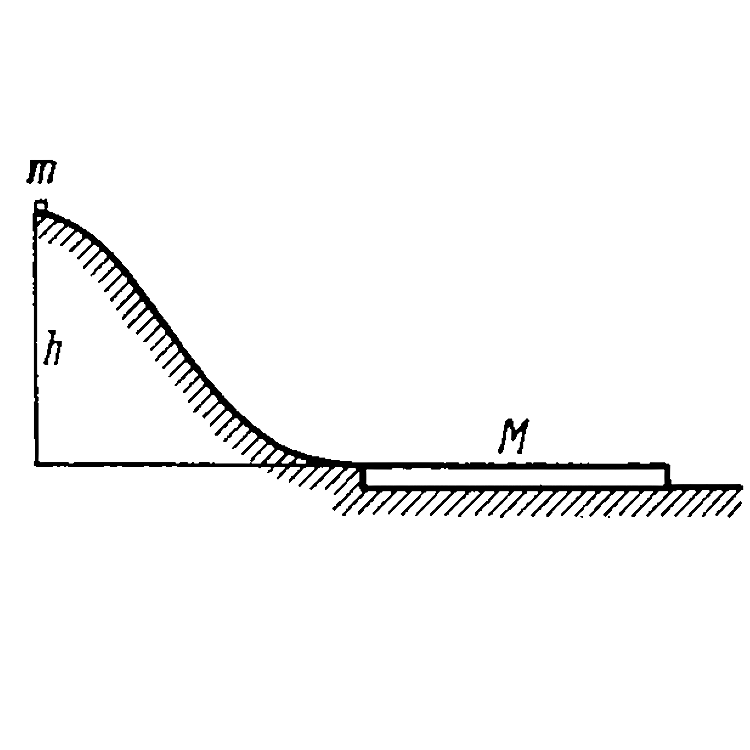
View Solution

A small disc of mass m slides down a smooth hill of height h without initial velocity and gets onto a plank of mass M lying on the horizontal plane at the base of the hill. (figure). Due to friction between the disc and the plank the disc slows down and, beginning with a certain moment, moves in one piece with the plank.
(1) Find the total work performed by the friction forces in this process.
(2) Can it be stated that the result of obtained does not depend on the choice of the reference frame?
ocr_image

View Solution

A particle of mass m is released from a certain height h with zero initial velocity. It strikes the ground elastlcally (direction of its velocity is reversed but magnitude remains the same). Plot the graph between its kinetic energy and time till it returns to its initial position.

View Solution

A model rocket rests on a frictionless horizontal surface and is joined by a string of length $l$ to a fixed point so that the rocket moves in a horizontal circular path of radius $l$ . The string will break if its tensiion exceeds a value $T$ . The rocket engine provides a thrust $F$ of constant magnitude along the rocket's direction of motion. the rocket has a mass $m$ that does not change with time. Answer the following questions based on the above passage.
What distance does the rocket travel between the time $t_{1}$ when the string breaks and the time $2 t_{1}$ ? The rocket engine continues of operate after the string breaks.

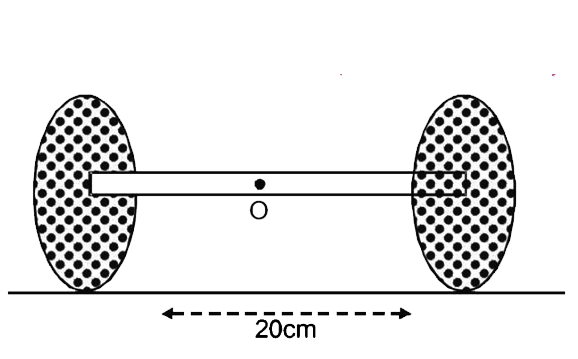
View Solution

Two thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of $9 m / s^{2}$ Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors $ˆ i, ˆ j and ˆ k$ in the x,y, and z directions.
ocr_image

View Solution

Momentum is the ability of imparting or tending to import motion to other bodies. The total momentum of a system remains conserved if no external force is acting it. This is calculated by the formula $\to p = m \to v$ .
Consider a situation where a cart carrying five boys is moving without friction due to inertia along a straight horizontal road, with a speed of 10 m/s. After travelling certain dfistance a boy jumps from the cart with a speed of 2 m/s with respect to cart in opposite direction to it. Then, second boy jumps with the same speed w.r.t. the cart, but in a perpendicular direction to the cart. The mass of the cart is 100 kg and mass of each boy is 20 kg.
Answer the following questions.
The speed of the cart after second boy jumps will

View Solution

A 100 kg block is started with a speed of $2.0 m s^{- 1}$ on a long, rough belt kept fixed in a horizontal position. The coefficient of kinetic friction between the block and the belt is 0.20. (a) calculate the change in the internal energy of the block-belt system as the block comes to a stop on the belt. (b) consider the situation from a frame of reference moving at $2.0 m s^{- 1}$ along the initial velocity of the block. as seen from this frame, the block is gently put on a moving belt and in due time the block starts moving with the belt at $2.0 m s^{- 1}$ , calculate the increase in the kinetic energy of the block as it stops slipping past the belt. (c ) find the work done in this frame by the external force holding the belt.

View Solution

Consider a block of mass m that slides down the different inclined planes having same base legth L and same coefficient of friction.
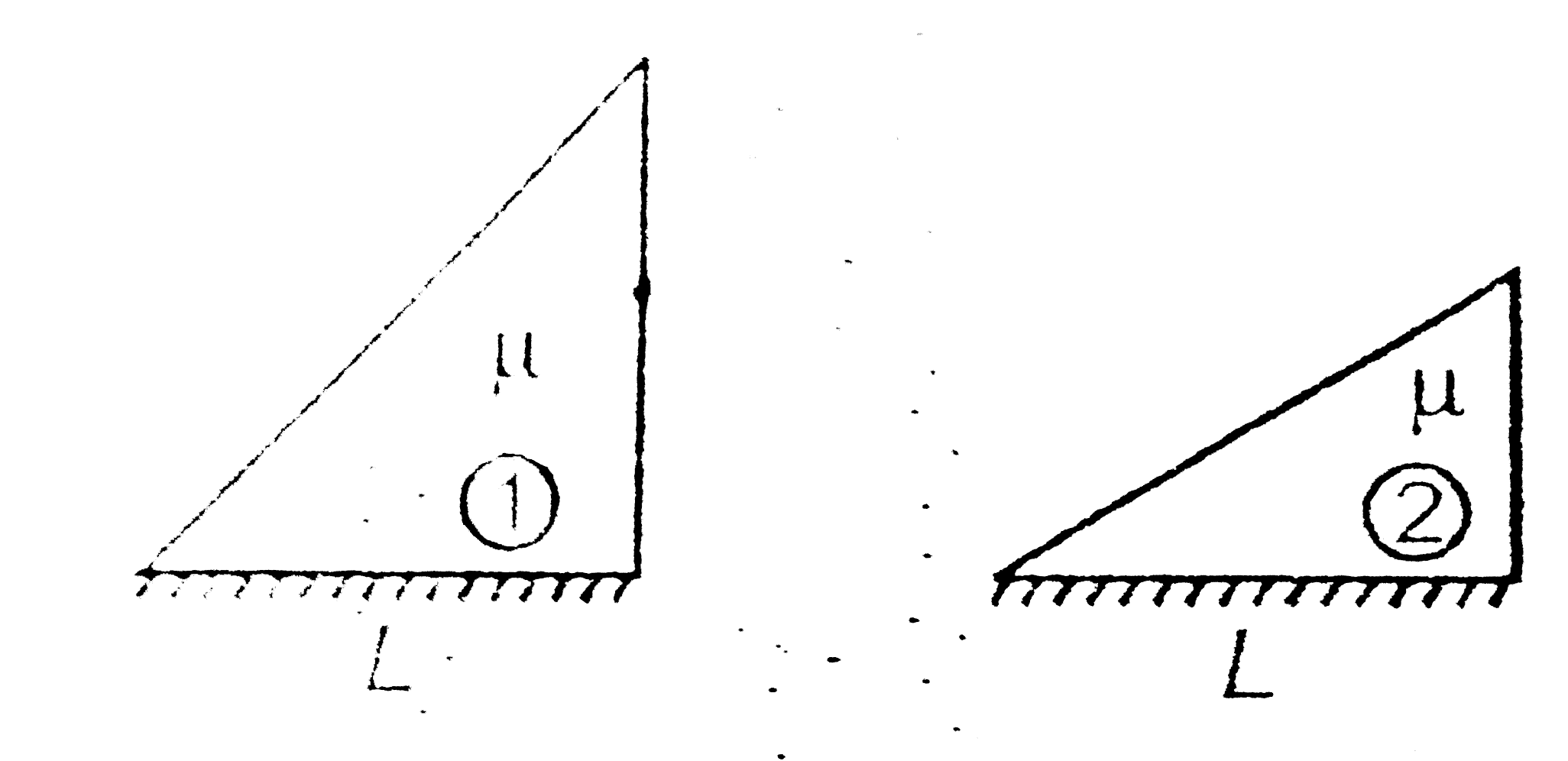
ocr_image
STATEMENT-1 Work done by force of friction will be same for the motion of the two inclined planes.
STATEMENT-2 Frictional force is a conservation force.

View Solution

A particle of mass $m$ is released from height $h$ on smooth quarter circular fixed wedge. The horizontal surface $A B$ following the circular path at bottom of wedge is rough with coefficient of friction $μ$ between surface and $m$ . Find the distance from bottom of wedge where the mass will stop.
ocr_image

View Solution

A projectile is fired with velocity u at an angle $θ$ with horizontal. At the highest point of its trajectory, it splits up into three segments of masses m, m and 2m. First part falls vertically downward with zero initial velocity and second part returns via same path to the point of projection. The velocity of third part of mass 2 m just after explosion will be

View Solution

The correct Answer is:D

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-WORK, POWER & ENERGY-Single Correct