An open knife of mass m is dropped from a height h on a wooden floor. If the blade penetrates up to the depth d into the wood. The average resistance offered by the wood to the knife edge is .
mg(1+hd)
mg(1+hd)2
mg(1−hd)
mg(1+dh)
The correct Answer is:A
To solve the problem of finding the average resistance offered by the wood to the knife edge, we can follow these steps:
Step 1: Understand the scenario
An open knife of mass m is dropped from a height h onto a wooden floor, and it penetrates a depth d into the wood. We need to find the average resistance force offered by the wood.
Step 2: Calculate the potential energy at the height
When the knife is at height h, it has potential energy given by:
PE=mgh
where g is the acceleration due to gravity.
Step 3: Determine the total distance fallen
When the knife hits the wooden floor and penetrates into the wood, the total distance fallen is the sum of the height h and the depth d:
htotal=h+d
Step 4: Calculate the work done during penetration
The work done by the knife while penetrating into the wood is equal to the force of resistance F multiplied by the distance d:
Work done=F⋅d
Step 5: Set the potential energy equal to the work done
At the moment of impact, the potential energy of the knife is converted into work done against the resistance of the wood. Therefore, we can equate the potential energy to the work done:
mgh=F⋅d
Step 6: Solve for the average resistance force F
Rearranging the equation to solve for F:
F=mghd
Step 7: Consider the total distance for average resistance
Since the knife penetrates a distance d, we can express the average resistance force as:
F=mg(h+d)d
This can be simplified to:
F=mg(1+hd)
Conclusion
Thus, the average resistance offered by the wood to the knife edge is:
F=mg(1+hd)
An open knife of mass m is dropped from a height h onto a wooden floor, and it penetrates a depth d into the wood. We need to find the average resistance force offered by the wood.
When the knife is at height h, it has potential energy given by:
PE=mgh
where g is the acceleration due to gravity.
When the knife hits the wooden floor and penetrates into the wood, the total distance fallen is the sum of the height h and the depth d:
htotal=h+d
The work done by the knife while penetrating into the wood is equal to the force of resistance F multiplied by the distance d:
Work done=F⋅d
At the moment of impact, the potential energy of the knife is converted into work done against the resistance of the wood. Therefore, we can equate the potential energy to the work done:
mgh=F⋅d
Rearranging the equation to solve for F:
F=mghd
Since the knife penetrates a distance d, we can express the average resistance force as:
F=mg(h+d)d
This can be simplified to:
F=mg(1+hd)
Thus, the average resistance offered by the wood to the knife edge is:
F=mg(1+hd)
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRANCE SPECIAL QUESTIONS
16 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MATCH THE COLUMNS
7 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.3
10 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
An open knife edge of mass 200g is dropped from height 5m on a cardboar. If the knife edge penetrates a distance 2 m into the cardboard. Find the average resistance offered by the cardboar to the knife edge (in N). (g=10m/s2)

View SolutionA particle of mass m is dropped from a great height h above the hole in the earth dug along its diameter.
View Solution
Knowledge Check
An open knife edge of mass M is dropped from a height h on a wooden floor. If the blade penetrates S into the wood, the average resistance offered by the wood to the blade is
AM gBM g (1+hs)CM g (1−hS)DM g (1+hS)2
An iron nail of mass m is dropped from a height h from level of a sand bed. If it penetrates through a distance x in the sand before coming to rest. Calculate the average force exerted by the sand on the nail. (Take g=10m/s2)
View SolutionHammer of mass M strikes a nail of mass 'm' with a velocity 20 m/s into a fixed wall. The nail penetrates into the wall to a depth of 1 cm. The average resistance of the wall to the penetration of the nail is
View SolutionA body of mass 'm is drhopped from a height 'h'. The speed with which body hits the ground is √0.9gh Find the work done by air-resistance furing its fall.
View SolutionA frequently used device to measure the speed of bullets is the ballistic pendulum. It comprises of a heavy block of wood of mass M suspended by two long chords. A bullet of mass m is fired into the block horizontally. The block, with the bullet embedded in it, swings upwards. The centre of mass of the combination rises through a vertical distance h before coming to rest momentarily. In a particular experiment, a bullet of mass 40 gm is fired into a wooden block of mass 10 kg. The block is observed to rise by a height of 20.0 cm.
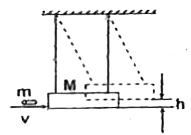
If the bullet penetrates the block to a depth of 3.0 cm, the approximate average force of resistance by the block of wood is
View SolutionA ball is dropped from a height of 5 m onto a sandy floor and penetrates the sand up to 10 cm before coming to rest. Find the retardation of the ball in and assuming it to be uniform.
View SolutionWhen a bullet of mass 10 g and speed 100 m/s penetrates up to distance 1 cm in a human body at rest. The resistance offered by human body is :
View SolutionA ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h<<R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is
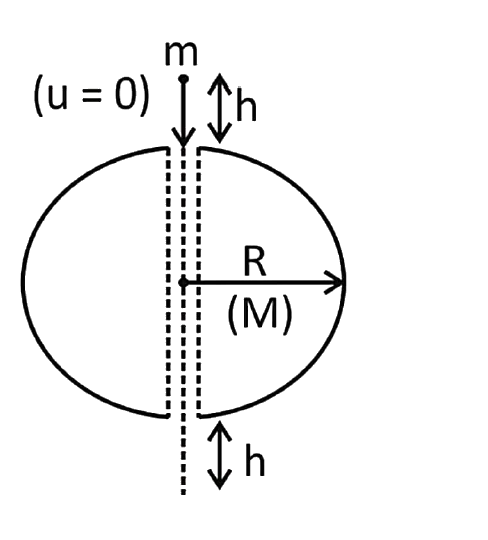
View Solution
