Answer question on the basis of your understanding of the following p

Which of the following characteristics of electrons determines the current in a conductor ?

Electric current density is a_______ quantity whereas electric current is a ______ quantity.

(a) Six lead-acid type of secondary cells each of emf 2.0 V and internal resistance 0.015 $Ω$ are joined in series to provide a supply to a resistance of 8.5 $Ω$ . What are the current drawn from the supply and its terminal voltage ?
(b) A secondary cell after long use has an emf of 1.9 V and a large internal resistance of 380 $Ω$ . What maximum current can be drawn from the cell ? Could the cell drive the starting motor of a car?

View Solution

(a) Using Gauss's law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
(b) The electric field components in the following figure are $E_{x} = α x, E_{y} = 0, E_{z} = 0$ , in which $α = 400 N / C m$ . Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that $a = 0.1 m$ .
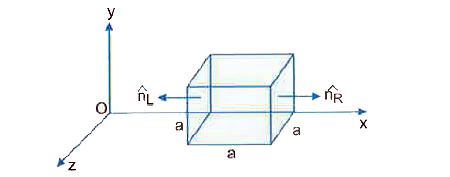ocr_image

View Solution

Define the term 'work function' of a metal. The threshold frequency of a metal is $f_{0}$ . When the light of frequency $2 f_{0}$ is incident on the metal plane, the maximum velocity of electrons is $v_{1}$ . When the frequency of the incident is increased to $5 f_{0}$ , the maximum velocity of electrons emitted is $v_{2}$ . find the ratio of $v_{1}$ to $v_{2}$ .

View Solution

A cylindrical copper conductor AB length $L$ areaa of cross-section a has large number of free electrons which at mean temperature move at random within the body of the conductor like the molecules of a gas. The average thermal motion at room temperature is of the enter of $10^{5} m s^{- 1}$ where a potential difference $V$ is applied free electronic in the condictior experience , the free electrons in the conductor experience force and are accelerated towards the positive emf of the condutor on their gained kinetic energy After each collision the free electronic are angle acceleration due of the electric field , towards the positive end the conductor and next collision with the ions/atoms of the electrons The average speed of the free electrons with which they drift toward the positive and of the conductor under the effect of applied electric field is called drift of the electrons
The speed of electrons in a conductor is small $(= 10^{- 4} m s^{- 1})$ when the switch is closed, the bulb at a distance glows immediately. It is so because

View Solution

Assertion : Free electrons inside a metal are free to move out of the metal. Reason : Free electrons inside conductor do not need additional energy to get out of the metal.

View Solution

Answer question on the basis of your understanding of the following paragraph and the related studied concepts :
Bulk matter is made up of many molecules, which are so closely packed that the electrons are no longer attached to individual nuclei. In metallic conductors some of the electrons are practically free to move within the bulk material. Ordinarily, the electrons will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random and there is no preferential direction for the velocities of the electrons. So number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction and there will be no net flow of electrons and hence no net current.
When an external electric field $\to E$ is applied across a piece of conductor, electrons will be accelerated at $\to a = \frac{e \to E}{m}$ . If $\to a$ was the velocity of electron after the last collision then velocity ${\to v}_{t}$ after a time t will be ${\to v}_{t} = \to u + \to a t$
The average velocity of the electrons at time t is the average of all $\to v'$ s. However, average value of $\to u'$ s is zero. As collisions of the electrons occur at random times, let $τ$ be the average time between successive collision and then the average velocity electrons is expressed as ${\to v}_{d}$ (known as the drift velocity) and is given as:
${\to v}_{d} = - \frac{e \to E}{m} τ$
This drift motion of electrons is responsible for establishment of an electric current in the conductor on applying an external electric field across it. The magnitude of current is given as : $I = n A e v_{d}$ , where n= number density of free electrons and A = cross-section area of the conductor. It is to be noted here that drift speed is estimated to be of the order of $10^{- 3} m s^{- 1}$ for currents in the range of a few amperes.
Define drift velocity. On what factors does it depend ?

04:40

View Solution

Answer question on the basis of your understanding of the following paragraph and the related studied concepts : Bulk matter is made up of many molecules, which are so closely packed that the electrons are no longer attached to individual nuclei. In metallic conductors some of the electrons are practically free to move within the bulk material. Ordinarily, the electrons will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random and there is no preferential direction for the velocities of the electrons. So number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction and there will be no net flow of electrons and hence no net current. When an external electric field vecE is applied across a piece of conductor, electrons will be accelerated at veca = (e vecE)/(m) . If veca was the velocity of electron after the last collision then velocity vec v_t after a time t will be vecv_t = vecu + veca t The average velocity of the electrons at time t is the average of all vec v' s. However, average value of vecu' s is zero. As collisions of the electrons occur at random times, let tau be the average time between successive collision and then the average velocity electrons is expressed as vecv_d (known as the drift velocity) and is given as: vecv_d = - (e vecE)/(m) tau This drift motion of electrons is responsible for establishment of an electric current in the conductor on applying an external electric field across it. The magnitude of current is given as : I = nAev_d , where n= number density of free electrons and A = cross-section area of the conductor. It is to be noted here that drift speed is estimated to be of the order of 10^(-3) ms^(-1) for currents in the range of a few amperes. If the electron drift speed is so small and the electron charge is small, how can we still obtain large amounts of current even in a thin conducting wire ?

View Solution

Answer question on the basis of your understanding of the following paragraph and the related studied concepts : Bulk matter is made up of many molecules, which are so closely packed that the electrons are no longer attached to individual nuclei. In metallic conductors some of the electrons are practically free to move within the bulk material. Ordinarily, the electrons will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random and there is no preferential direction for the velocities of the electrons. So number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction and there will be no net flow of electrons and hence no net current. When an external electric field vecE is applied across a piece of conductor, electrons will be accelerated at veca = (e vecE)/(m) . If veca was the velocity of electron after the last collision then velocity vec v_t after a time t will be vecv_t = vecu + veca t The average velocity of the electrons at time t is the average of all vec v' s. However, average value of vecu' s is zero. As collisions of the electrons occur at random times, let tau be the average time between successive collision and then the average velocity electrons is expressed as vecv_d (known as the drift velocity) and is given as: vecv_d = - (e vecE)/(m) tau This drift motion of electrons is responsible for establishment of an electric current in the conductor on applying an external electric field across it. The magnitude of current is given as : I = nAev_d , where n= number density of free electrons and A = cross-section area of the conductor. It is to be noted here that drift speed is estimated to be of the order of 10^(-3) ms^(-1) for currents in the range of a few amperes. Are the paths of electrons straight lines between successive collisions in the (i) absence of electric field, (ii) presence of electric field ?

01:30

View Solution

Answer question on the basis of your understanding of the following paragraph and the related studied concepts :
Bulk matter is made up of many molecules, which are so closely packed that the electrons are no longer attached to individual nuclei. In metallic conductors some of the electrons are practically free to move within the bulk material. Ordinarily, the electrons will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random and there is no preferential direction for the velocities of the electrons. So number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction and there will be no net flow of electrons and hence no net current.
When an external electric field $\to E$ is applied across a piece of conductor, electrons will be accelerated at $\to a = \frac{e \to E}{m}$ . If $\to a$ was the velocity of electron after the last collision then velocity ${\to v}_{t}$ after a time t will be ${\to v}_{t} = \to u + \to a t$
The average velocity of the electrons at time t is the average of all $\to v'$ s. However, average value of $\to u'$ s is zero. As collisions of the electrons occur at random times, let $τ$ be the average time between successive collision and then the average velocity electrons is expressed as ${\to v}_{d}$ (known as the drift velocity) and is given as:
${\to v}_{d} = - \frac{e \to E}{m} τ$
This drift motion of electrons is responsible for establishment of an electric current in the conductor on applying an external electric field across it. The magnitude of current is given as : $I = n A e v_{d}$ , where n= number density of free electrons and A = cross-section area of the conductor. It is to be noted here that drift speed is estimated to be of the order of $10^{- 3} m s^{- 1}$ for currents in the range of a few amperes.
Guess the order of magnitude of thermal speed of free electrons in a conductor in the absence of an external electric field.

View Solution

Define relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons ? Use this relation to deduce the expression for the electrical resistivity of the material.

View Solution

Define relaxation time of the free electrons drifting in conductor. How is it related to the drift velocity of free electrons? Use this relation to deduce the expression for the electrical resistivity of the material.

01:58

View Solution

The high thermal conductivity of metal is due to free electrons. The relevant electron property is :

View Solution

Assertion : Free electrons inside a metal are free to move out of the metal.
Reason : Free electrons inside conductor do not need additional energy to get out of the metal.

01:45

View Solution

Electric field (or electrical energy) leavels at the speed of light $(c = 3 \times 10^{8} m s^{- 1})$ inside the conductor.

Topper's Solved these Questions

Similar Questions

U-LIKE SERIES-CURRENT ELECTRICITY -CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS

Electric field (or electrical energy) leavels at the speed of light (c=3×108ms−1) inside the conductor.

Topper's Solved these Questions

Similar Questions

U-LIKE SERIES-CURRENT ELECTRICITY -CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS

Electric field (or electrical energy) leavels at the speed of light $(c = 3 \times 10^{8} m s^{- 1})$ inside the conductor.