(a) Using Gauss's law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
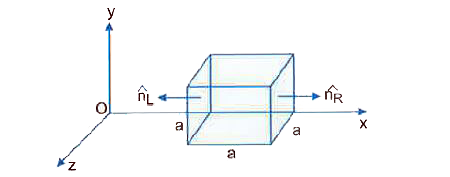
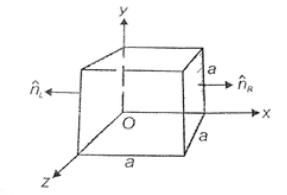
(b) The electric field components in the following figure are , in which . Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that .
(a) Consider an infinitely long straight charged wire of linear charge density . To find electric field at a point P situated at a distance r from the wire by using Gauss. law consider a cylinder of length l and radius r as the Gaussian surface.
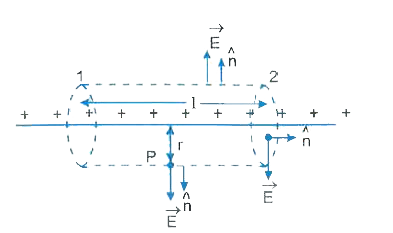
From symmetry consideration electric field at each point of its curved surface is and is pointed outwards normally. Therefore, electric flux over the curved surface
On the side faces 1 and 2 of the cylinder normal drawn on the surface is perpendicular to electric field E and hence these surfaces do not contribute towards the total electric flux.
Net electric flux over the entire Gaussian surface
By Gauss law electric flux
Comparing (i) and (ii), we have
(b) (i) Here, . So the electric flux is linked with only two fa c es of the cube lying in Y -Z plane (i.e., perpendicular to ).
As position of left face of cube is at , hence (inward into the Cube)
Now position of right face of cube is ,
hence .
Net flux
Net flux through the cube outward
(ii) Charge within the cube
Topper's Solved these Questions
- CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)EXERCISE - SECTION C
8 Videos
- CBSE EXAMINATION PAPER 2020 (SOLVED) BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (SOLVED) EXERCISE - SECTION - D
6 Videos
- CURRENT ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - CURRENT ELECTRICITY EXERCISE - SELF ASSESSMENT TEST (SECTION C )
3 Videos
Similar Questions
Using Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
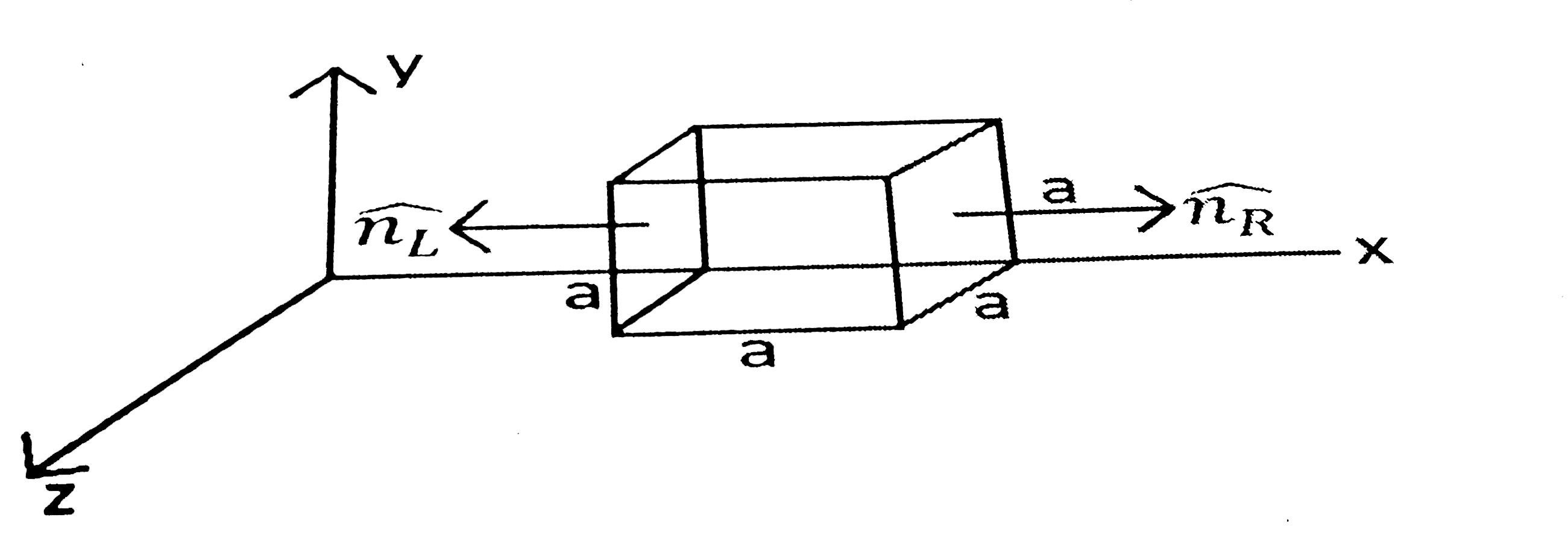
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
View SolutionUsing Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.

View Solution
Knowledge Check
The electric components in the figure are Ex=αx1/2,Ey=0,Ez=0 where α=800N/m2 if a=0.1m is the side of cube then the charge with in the cube is
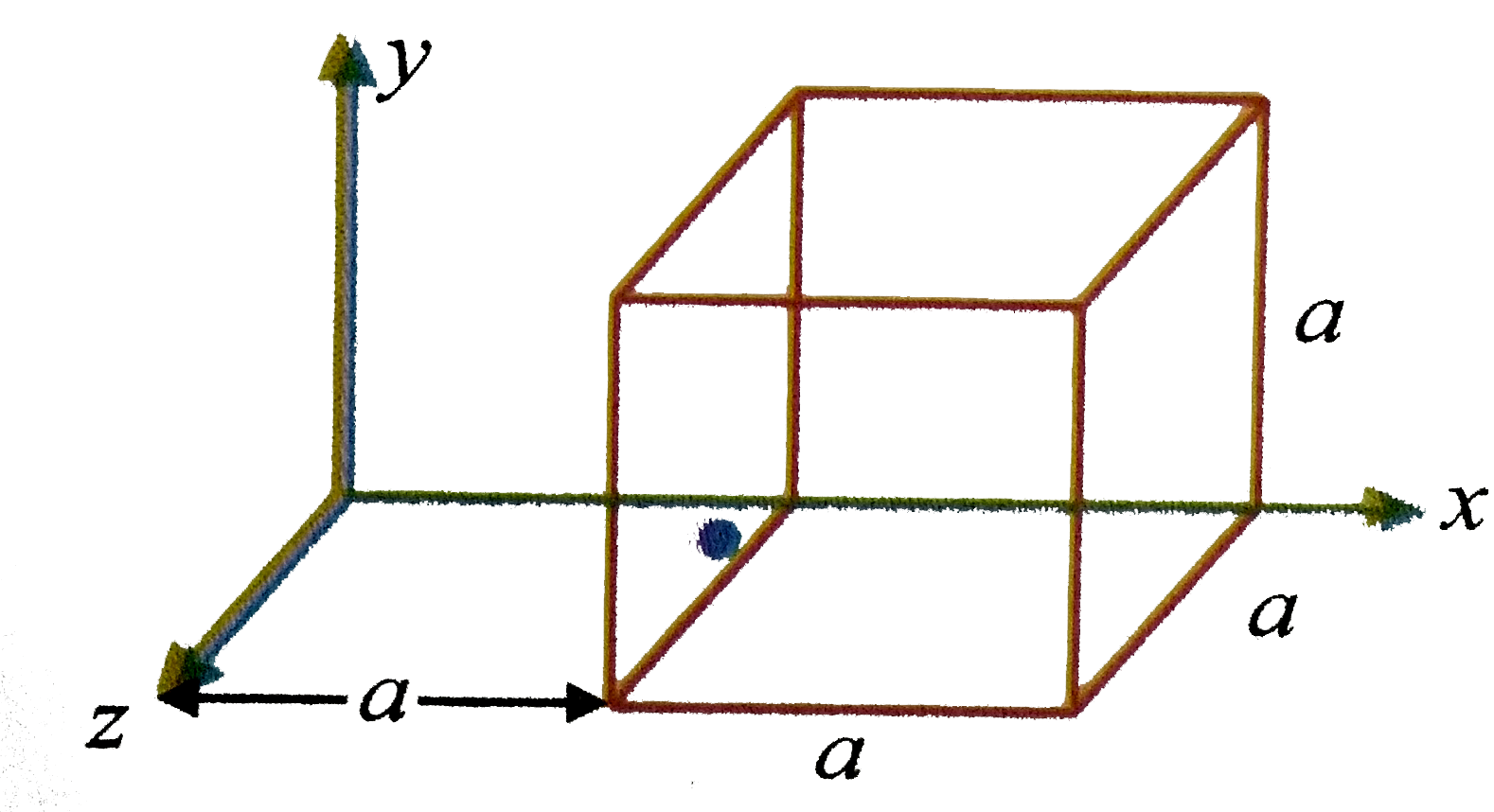 A9.27×10−12CB6×10−12CC2.5×10−12CDZero
A9.27×10−12CB6×10−12CC2.5×10−12CDZero
Using Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
View SolutionUsing Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
View SolutionUsing Gauss's law, derive an expression for the electric field intensity at any point near a uniformly charged thin wire of charge/length=λC/m.
View SolutionThe electric field components in the figure below are Ex=800x2N/C,Ey=Ez=0.
Calculate
(1) The flux throught he cube and
(2) The charge withing the cube
Assume that a =0.1 m
View SolutionThe electric components in the figure are Ex=αx1/2,Ey=0,Ez=0 where α=800N/m2 if a=0.1m is the side of cube then the charge with in the cube is
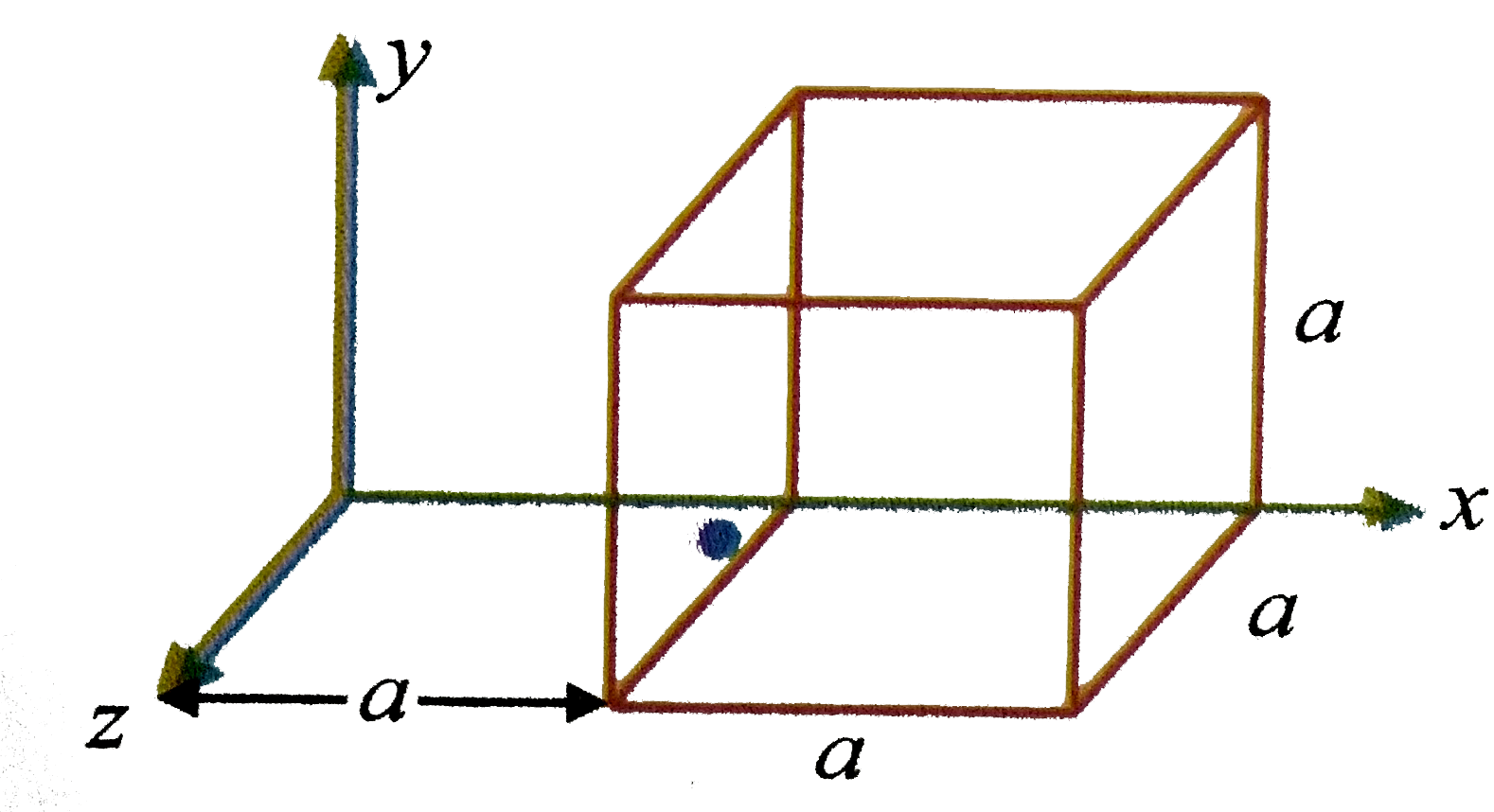
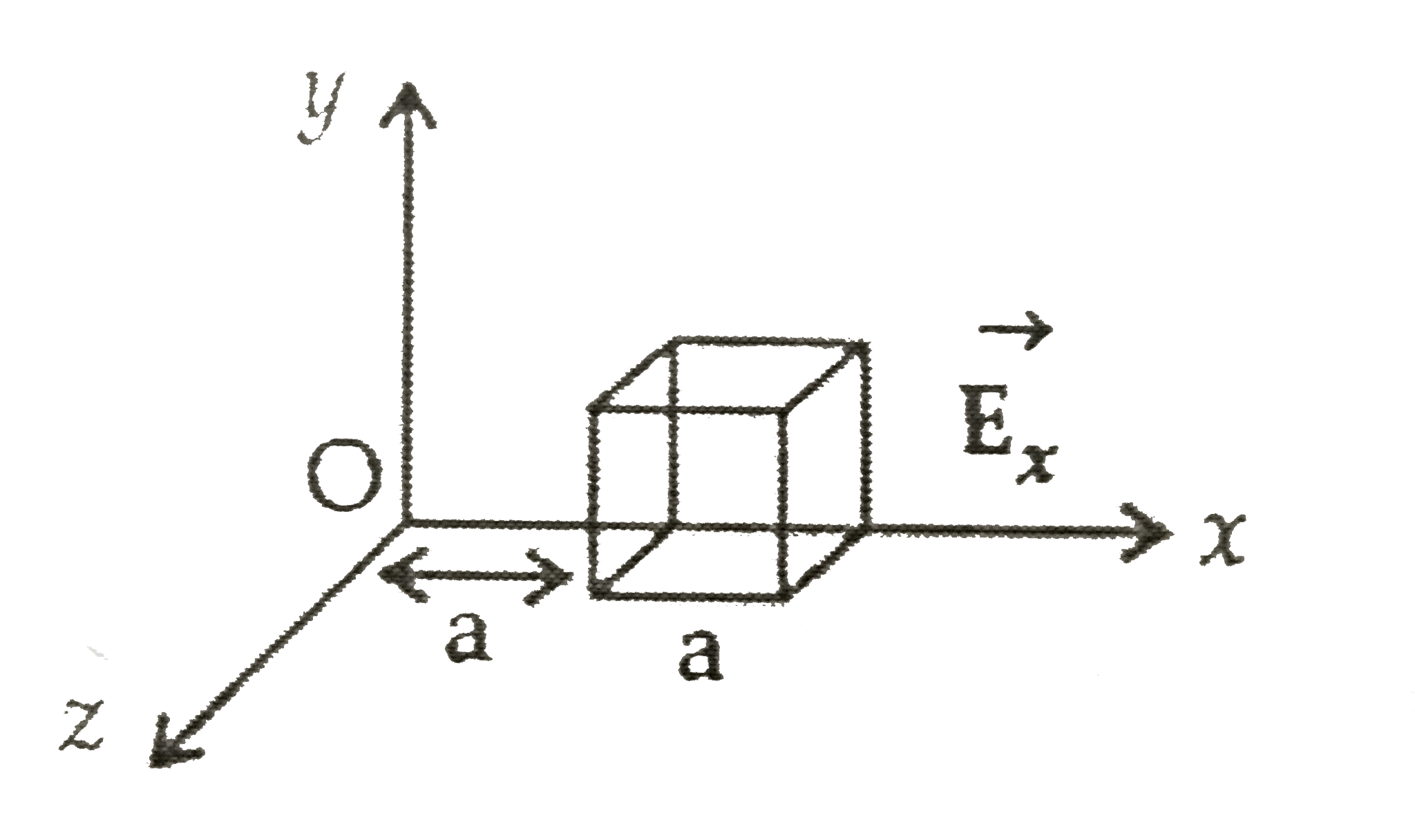
View SolutionDefine electric flux and write its SI unit . The electric field components in the figure shown are : Ex=αx,Ey=0,Ez=0 where α=100NCm.
Calculate the charge within the cube , assuming a = 0.1 m .
View SolutionDefine electric flux and write its SI unit . The electric field components in the figure shown are : Ex=αx,Ey=0,Ez=0 where α=100NCm.
Calculate the charge within the cube , assuming a = 0.1 m .

View Solution
