Using Gauss's law obtain the expression for the electric field due to uniformly charged thin spherical shell of radius R at a point outside the shell. Draw a graph showing the variation of electric tield with r, for r gt R and r lt R.
Electric fieldout side the shell (r→R).
Let we have a spherical shell having +q charge on the surface, we have choosen a spherical Gaussian surface S. According to Gauss's theorem
ϕ=∮s→E.→ds=9∈0
∮scos0∘=q∈0⎧⎪⎨⎪⎩E is constant∮ds=4πr2cos0∘=1
E(4πr2)(1)=q∈0, E=14π∈0qr2
It's equal to the electric field due to a point charge.
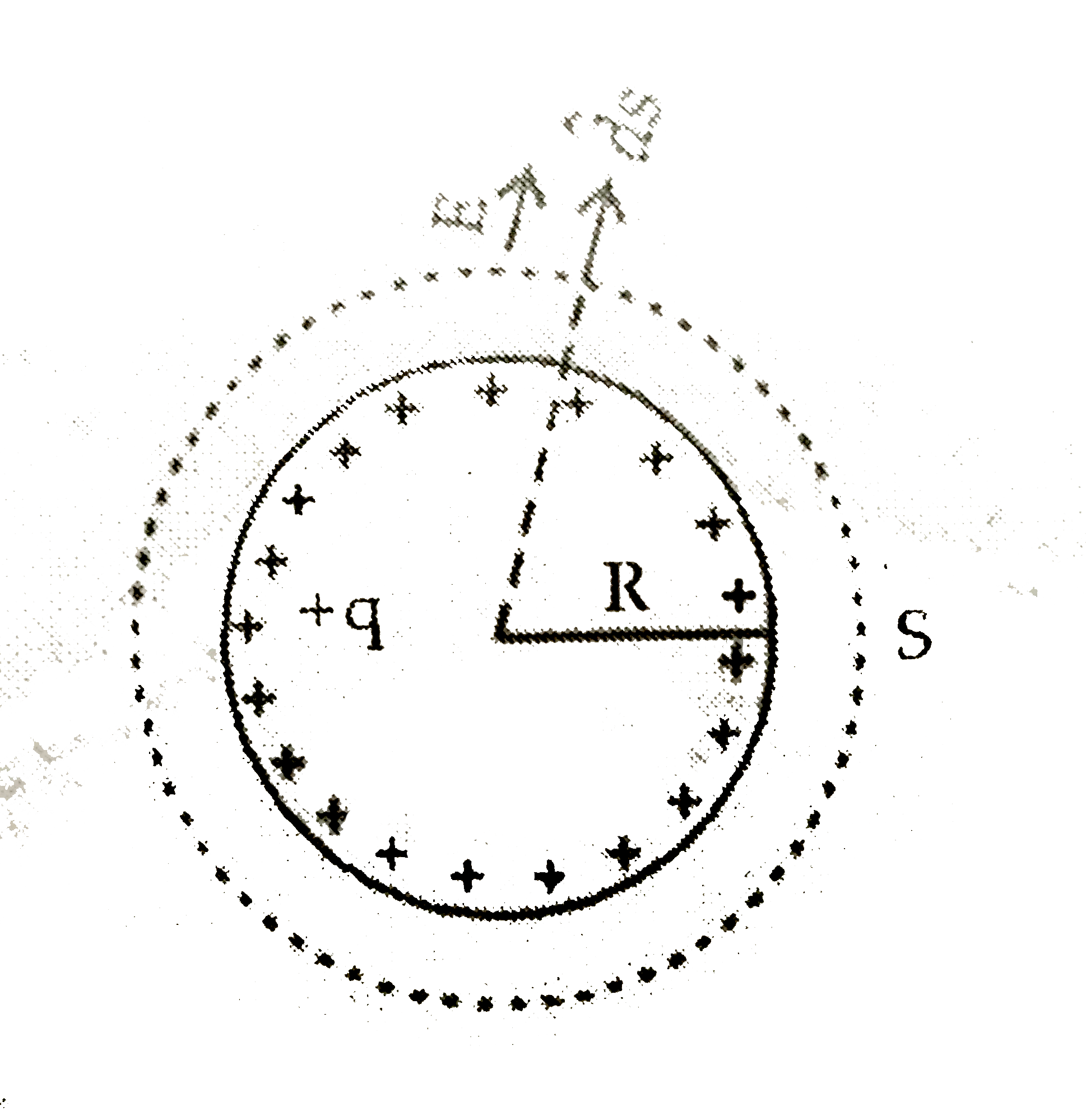
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
AQ4πε0r for points outside and Q4πε0R for points inside the shellBQ4πε0e for both points inside nad outside the shellCzero for points outside and Q4πε0r for points inside the shellDzero for both points inside and outside the shell
Using Gauss' law deduce the expression for the electric field due to uniformaly charged spherical conducting shell of radius R at point (i) outside ,and (ii) inside the shell.
Plot a graph showing variation of electric field as a functions or r for r< R and .(r being the distance from the centre of the shell).View SolutionFind out energy stored in the electric field of uniformly charged thin spherical shell of total charge Q and radius R.
View SolutionUsing Gauss's theorem derive an expression for the electric field at any point outside a charged spherical shell of radius R and of charge density σC/m2
View SolutionUsing Gauss's law derive an expression for the electric field at any point outside a uniformaly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charges density of the sphere is (i) positive (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100μC/m2 Calculate the
(i) charge on the sphere (ii) total electric flux passing through the sphere.View Solution(a) Use Gauss's law to show that due to a uniformly charged spherical shell of radius R, the electric field at any point situated outside the shell at a distance r from its centre is equal to the electric field at the same point, when the entire charge on the shell were concentrated at its centre. Also plot the graph showing the variation of electric field with r, for r≤R and r≥R. (b) Two point charges of +1μC and +4μC are kept 30 cm apart. How far from the +1μC charge on the line joining the two charges, will the net electric field be zero ?
View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.View SolutionUsing Gauss’s theorem in electrostatics, deduce an expression for electric field intensity due to a charged spherical shell at a point (i) inside (ii) on its surface (iii) outside it. Graphically show the variation of electric field intensity with distance from the centre of shell.
View Solution

