Question

Using Gauss's theorem derive an expression for the electric field at any point outside a charged spherical shell of radius R and of charge density $\sigma C/m^2$

Explanation

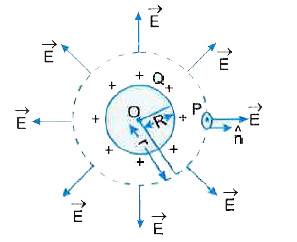
Consider a uniformaly charged thin spherical shell of radius R and having a charge Q. To find electric field at a point outside the shell situated at a distance (` r gt R ) ` from the centre of shell, consider a sphere of radius r as the Gaussian surface. All points on this surface are equivalent relative to given charged sheel and,thus electric ` oversetto E ` at all points of Gaussian surface has same magnitude `oversetto E and hat n ` are parallel to each other.
` therefore ` Total electric flux over the Gaussian surface
` phi _in = int oversetto E hat n ds = E . 4 pi r^(2) " " ...(i) `
According to Gauss.s theorem
` phi _in =(1)/( in _0) ` ( charged enclosed) ` = (Q)/( in _0) " "...(ii) `
Comparing (i) and ( ii) ,we get
` E. 4 pi r^(2) =(Q)/( in_0) or E =(Q)/( 4 pi in _0 r^(2)) `
Thus , for any point outside the shell, the effect is, as if whole charge Q is concentrated at the centre of teh spherical shell.
If surface charge density of shell be ` sigma ` then Q = ` 4 pi R ^(2) sigma ` and therefore
` E= ( 4 pi R ^(2) sigma)/( 4 pi in_0 r^(2)) =( sigma R^(2))/( in _0 r^(2)) `