Applying Gauss's law derive the expression for electric intensity due to a charged conducting spherical shell at (i) a point outside the shell (ii) a point on the surface of the shell and (iii) a point inside the shell.Solution in Telugu
Expression for E due to a charged conducting spherical shell :
(1) Consider a uniformly charged spherical shell. Let total charge on it is 'q' and its radius is R.
Surface charge density σ=Total chargeSurface area=q4πR2 ...(1)
(2) Since the shell is uniformly charged, the intensity of electric field at any point depends on radial distance 'r' from centre 'O'. The direction of E is aways from the centre along the radius.
(i) E at a point outside the shell :
(1) Consider a point at a distance 'r' outside the sphere. Construct a Gaussian surface with 'r' as radius (where r>R).
(2) Total flux coming out of this sphere is ϕ=→E∮.d→s=E∮ds=qε0.
But ∮SdS= Area of sphere =4πr2
∴E.4πr2=qε0
But q=4πR2σ (from equation 1)
∴E=14πr24πR2σε0
(3) Therefore at any point outside the sphere, E=σε0R2r2
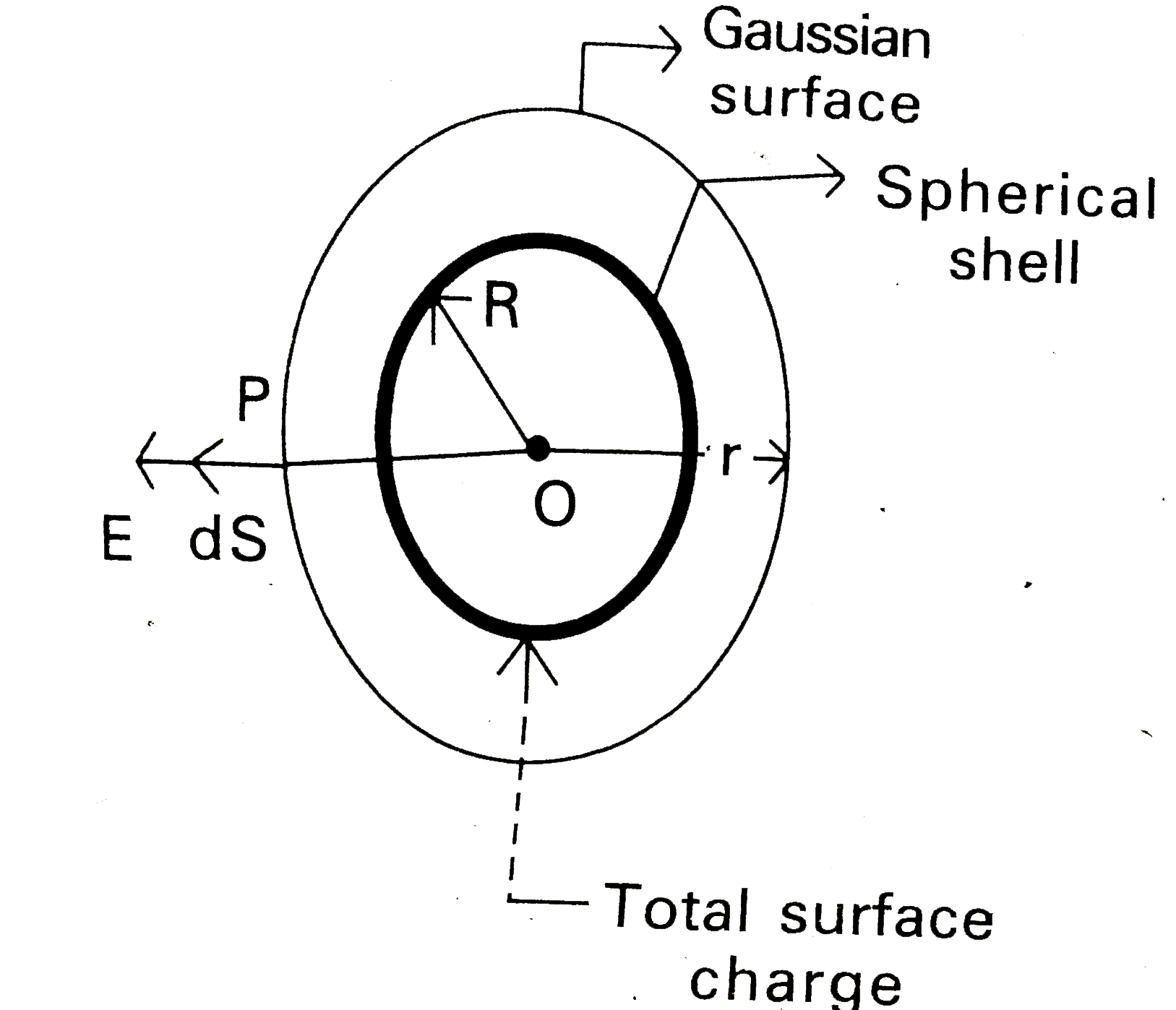
(ii) E at a point on the surface of shell :
(1) Construct a Gaussian surface with radius r=R.
(2) Total flux through this sphere ϕ=∮→E.d→S=E∮SdS=qε0.
But ∮dS of sphere =4πR2 and q=4πR2σ
⇒E.4πR2=4πR2σε0=4πR2σε0⇒E=σε0
(3) Therefore intensity at any point on surface of the sphere E=σε0

(iii) E at a point inside the shell :
(1) Consider a point P inside the shell. Construct a Gaussian surface with radius r (where r<R). There is no charge inside the shell. So form Gauss's law ∮S→E.d→S=qε0.
But q=0⇒∮S→E.d→S=E.4πr2=0.
(2) Therefore, intensity of electric field at any point inside a charged shell is zero.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - TEXTUAL EXERCISES
11 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - ADDITIONAL EXERCISES
53 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - SHORT ANSWER QUESTIONS
6 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - DAM SURE (VSAQ)
2 Videos
- ELECTROMAGNETIC INDUCTION BOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - Additional EXERCISES
15 Videos
Similar Questions
Two small identical balls, each of mass 0.20 g, carry identical charges and are suspended by two threads of equal lengths. The balls position themselves at equilibirum such that the angle between the threads is 60∘. If the distance between the balls is 0.5 m, find the charge on each ball.
View SolutionWhat is the force between two small charged soheres having charges of 2×10−7C and 3×10−7C placed 30 cm apart in air ?
View SolutionState and explain Coulomb's incerse square law in electricity.
View SolutionThe wavelength of electromagnetic radiation is doubled. What will happen to the energy of the photons of the new radiation ?
View SolutionSuppose the loop in Textual Exercise 4 is stationary but the current feeding the electromagnet that produces the magnetic field is gradually reduced so that the field decreases from its initial value of 0.3 T at the rate of 0.02Ts−1 .If the cut is joined and the loop has a resistance of 1.6Ω how much power is dissipated by the loop as heat ? What is the source of this power ?
View Solutionएकसमान आवेशित गोलीय कोश के कारण वैधुत क्षेत्र की तीव्रता का व्यंजक ज्ञात कीजिए जबकि बिन्दु कोश के ( i ) बाहर, ( ii ) पृष्ठ पर, ( iii ) अन्दर स्थित है ।
View SolutionWrite the expression for electric intensity due to a charged conducting spherical shell at points outside and inside the shell.
View SolutionUsing Gauss' law deduce the expression for the electric field due to a uniformly charge spherical conducting shell of radius R at a point (i) outside the shell.
View SolutionUsing Gauss's law in electrostatics, obtain an expression for electric field due to a uniformly charged thin spherical shell at a point (i) Outside the shell and (ii) Inside the shell
View SolutionState Gauss's law. Derive an expression for electric intensity at a point outside the uniformly charged shell.
View SolutionUsing Gauss's law in electrostatics, obtain an expression for electric field due to a uniformly charged thin spherical shell at a point
(i) Outside the shell and
(ii) Inside the shell
View SolutionDerive an expression for electric intensity E due to a uniformly charged thin spherical shell at a point outside the shell.
View SolutionFind expression for electric field intensity due to a uniformly charged thin spherical shell at a point outside the shell.
View SolutionState Gauss's theorem. Obtain an expression for elactric field at any point outside a charged spherical hollow conductor (shell).
View SolutionState Gauss's theorem with the help of diagram, derive an expression for the electric field intensity due to uniformly charged thin spherical shell at a point on the surface of the spherical shell.
View Solution
