Using Gauss's law in electrostatics, obtain an expression for electric field due to a uniformly charged thin spherical shell at a point
(i) Outside the shell and
(ii) Inside the shell Solution in Kannada
Gauss.s theorem : The total outward electric flux passing through a closed surface in air is (1ε0) times the total charge enclosed by it . .
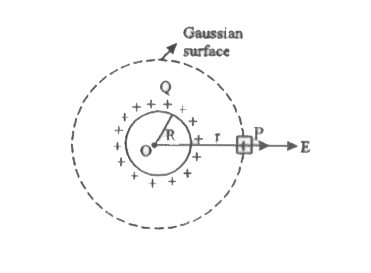
Let .+Q. be the charge enclosed by a hollow conductor of radius .R..
Let .p. be a point at a distance .r. from the centre of the conductor and .ds. be a small element of area surrounding the point . A normal drawn from the point coincides with the direction of →E. Hence cos 0∘=1.
From Gauss.s theorem ,
TOEF=ϕ=(1ε0)Q...(1)
by definition f=E cos q Sds.
where, ads=4pr2,cosq=cos0∘=1
hence, f=E . 4pr2...(2)
Comparing (1) & (2)
we write E=(14πε0)Qr2
For a point on the surface , r =R
E=(14πε0)(QR2)
This electric field intensity is maximum . Since electric flux depends on the charge enclosed and electric field intensity depends on the electric flux , electric field remains zero at all points inside the spherical hollow conductor.
Topper's Solved these Questions
- SUPER MODEL QUESTION PAPER -5BOOK - SUBHASH PUBLICATIONCHAPTER - SUPER MODEL QUESTION PAPER -5EXERCISE - PART -D
8 Videos
- SUPPLEMENTARY EXAMINATION QUESTION PAPER (WITH ANSWER) JULY-2018BOOK - SUBHASH PUBLICATIONCHAPTER - SUPPLEMENTARY EXAMINATION QUESTION PAPER (WITH ANSWER) JULY-2018EXERCISE - PART-D
12 Videos
Similar Questions
Obtain an expression for the electric field intenstiy at a point on the equatorial line of an electric dipole.
View SolutionUsing Gauss's law in electrostatics, obtain an expression for electric field due to a uniformly charged thin spherical shell at a point
(i) Outside the shell and
(ii) Inside the shell
View Solutionएकसमान आवेशित गोलीय कोश के कारण वैधुत क्षेत्र की तीव्रता का व्यंजक ज्ञात कीजिए जबकि बिन्दु कोश के ( i ) बाहर, ( ii ) पृष्ठ पर, ( iii ) अन्दर स्थित है ।
View SolutionApplying Gauss's law derive the expression for electric intensity due to a charged conducting spherical shell at (i) a point outside the shell (ii) a point on the surface of the shell and (iii) a point inside the shell.
View SolutionUsing Gauss' law deduce the expression for the electric field due to a uniformly charge spherical conducting shell of radius R at a point (i) outside the shell.
View SolutionUsing Gauss' law deduce the expression for the electric field due to a uniformly charge spherical conducting shell of radius R at a point (ii) inside the shell.
View SolutionUsing Gauss's law in electrostatics, obtain an expression for electric field due to a uniformly charged thin spherical shell at a point (i) Outside the shell and (ii) Inside the shell
View SolutionDerive an expression for electric intensity E due to a uniformly charged thin spherical shell at a point outside the shell.
View SolutionFind expression for electric field intensity due to a uniformly charged thin spherical shell at a point outside the shell.
View SolutionState Gauss's theorem. Obtain an expression for elactric field at any point outside a charged spherical hollow conductor (shell).
View SolutionState Gauss's theorem in electrostatics. Apply this theorem to derive an expression for electric field intensity at a point outside a uniformly charged thin spherical shell.
View SolutionState Gauss's theorem with the help of diagram, derive an expression for the electric field intensity due to uniformly charged thin spherical shell at a point on the surface of the spherical shell.
View SolutionDerive an expression for electric field due to a uniformly charged spherical shell. i) at a point outside the shell
View SolutionDeduce the expression of field at P due to a uniformly charged thin spherical shell when the point,P is inside the shell.
View SolutionDerive the expression for electric field intensity due to a uniformly charged thin spherical shell at a point outside the shell
View Solution
