Figure shows a particle mass m=100g attaches with four identical spring , each of length l=10cm . Initial tension in each spring is F0=25N. Neglecting gravity , Calculate the period of small oscillation of the particle along a line perpendicular to the plane of the figure .
The correct Answer is:100
Step by step video, text & image solution for Figure shows a particle mass m = 100g attaches with four identical spring , each of length l = 10 cm . Initial tension in each spring is F_(0) = 25 N. Neglecting gravity , Calculate the period of small oscillation of the particle along a line perpendicular to the plane of the figure . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
figure shown a partical mass m=100g attaches with four identical spring , each of length l=10cm . Initical tension in each spring is F0=25N. Neglecting gravity , Calculate the period of small obscillation of the article along a line perpenducular to the plane of the figure .
View SolutionA small particle is tied by the help of two strings to vertical walls with the parameters as shown in the figure (g=π2). The time period of the small oscillations of the particle if it is displaced perpendicular to the plane of the paper slightly is x sec, the value of x is ____________
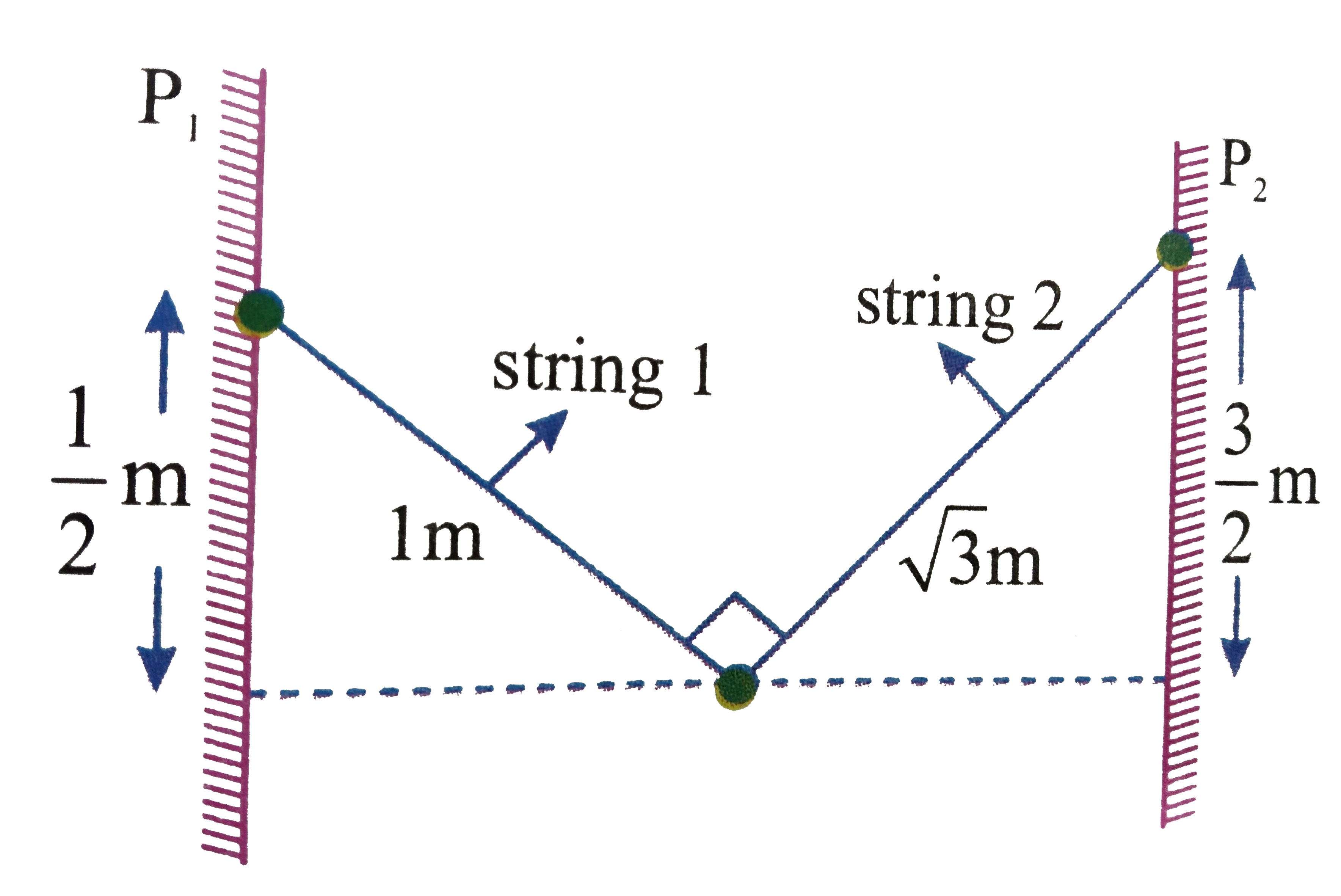
View Solution
Knowledge Check
- Question 1 - Select One
The following figure shows a particle of mass, m, attached with four identical springs, each of length l. Initial tension in each spring is F0. The period of small oscillations of the particle along a line perpendicular to the plane of the figure is (neglect gravity)
Aπ√mlF0B2π√mlF0C2π√ml2F0Dπ√ml4F0 - Question 2 - Select One
A particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
A2π√mkB2π√m2kC2π√m3kDπ√mk - Question 3 - Select One or More
The figure shows the arrangement of block of mass m with one or more identical springs in three different ways . If Force cosntant of each springs is K and T1, T2 and T3 are the time periods of oscillations of the arrangement 1, 2, and 3, respectibely, then
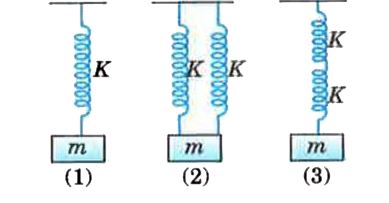AT2=1√2T1BT3=√2Tt1CT3=2T2DT3=√2T2
A particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
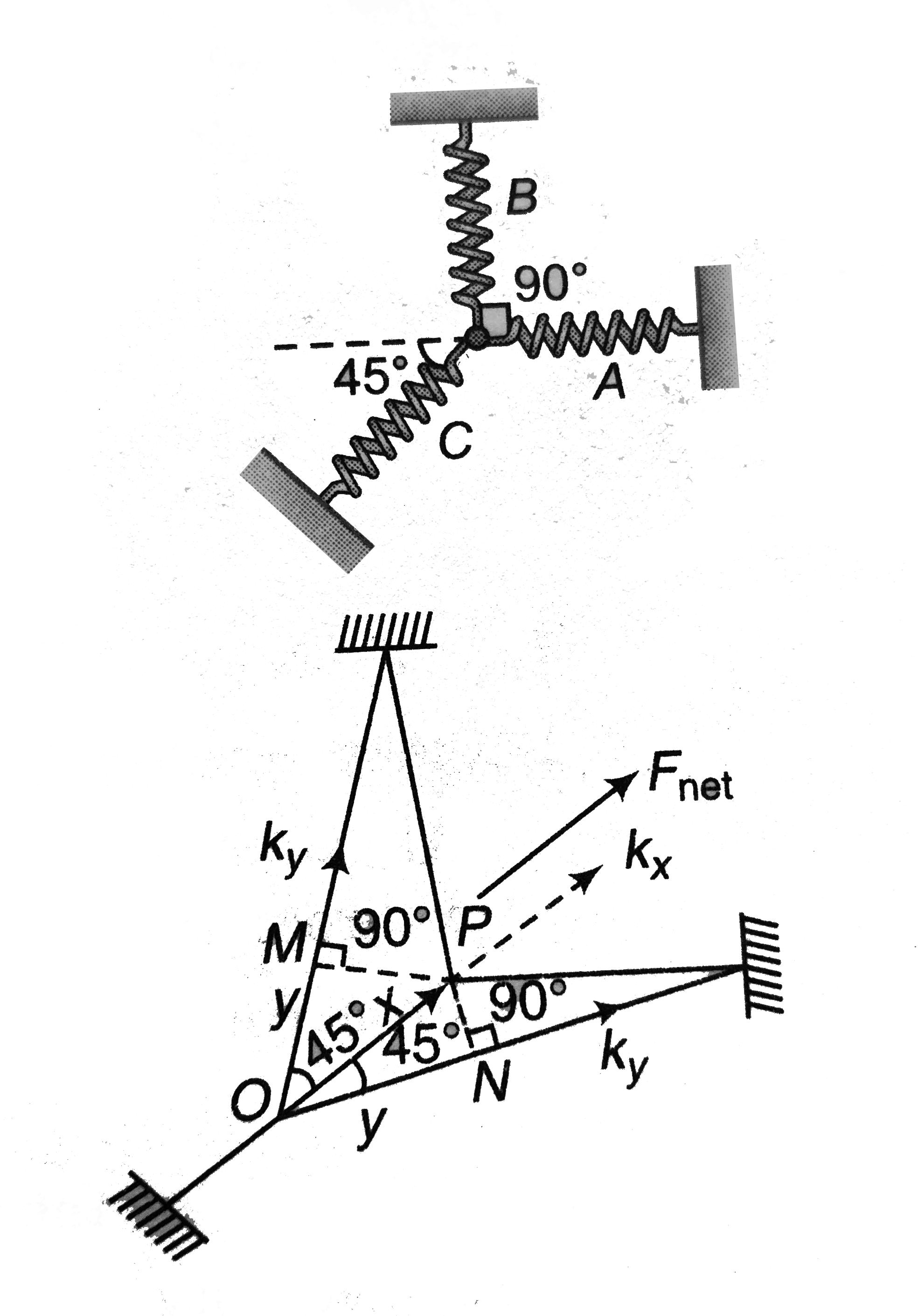. View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
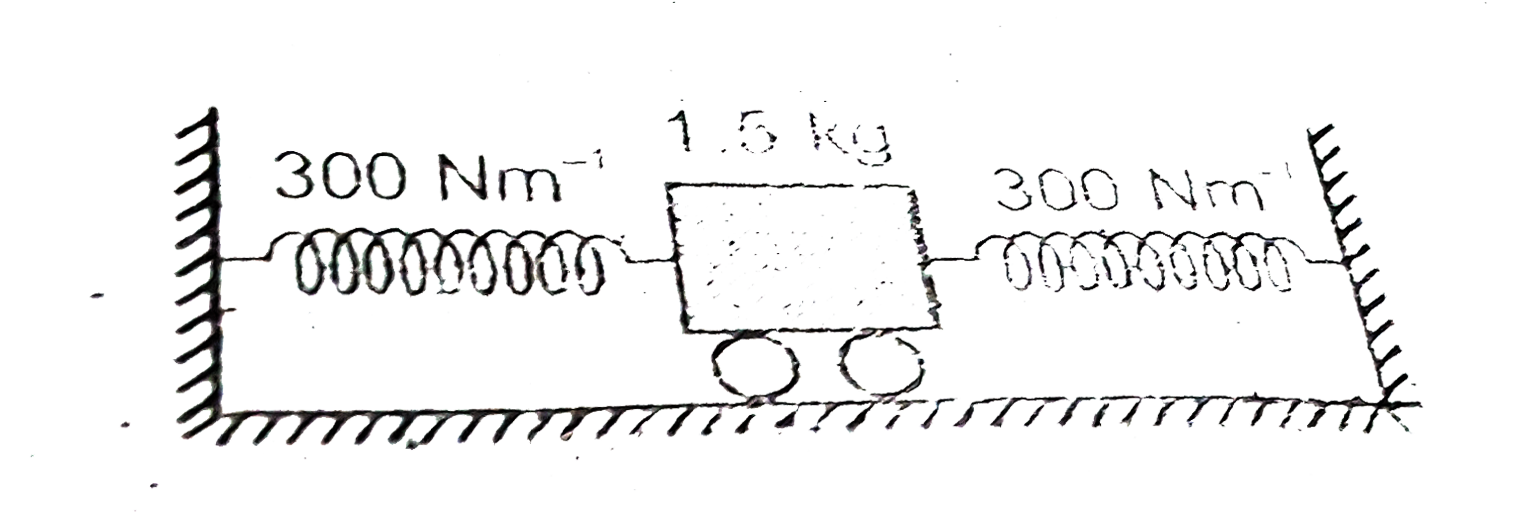
View SolutionA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
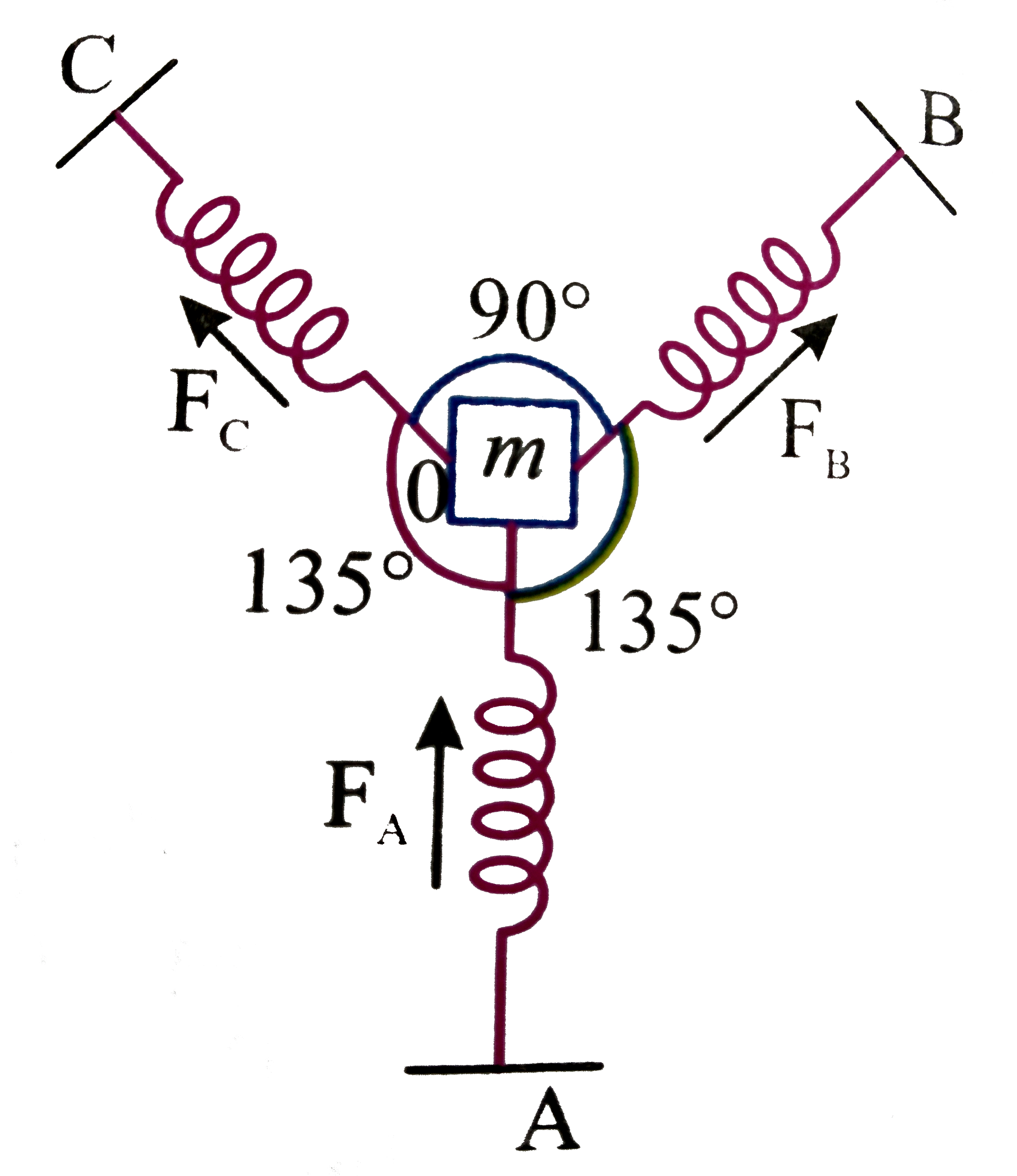
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
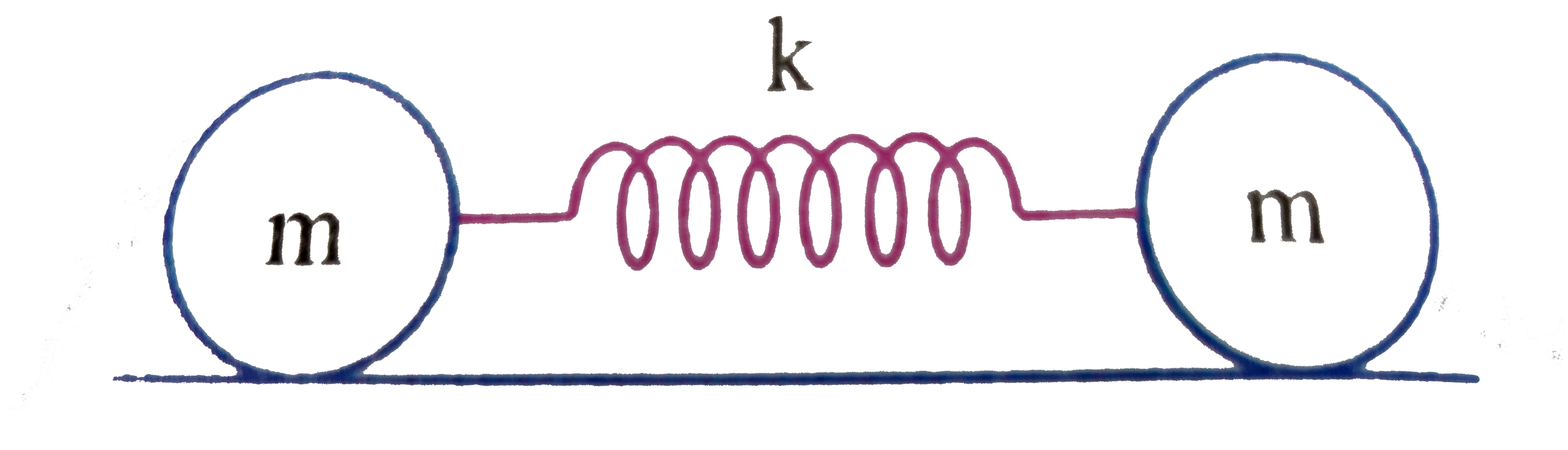
View SolutionTwo identical particles each of mass 0.5kg are interconnected by a light springs of stiffness 100N/m, time period of small oscillation is ….
View Solution