Asseration: The magnetic flux through a loop of conducting wire of a fixed resistance changes by ΔϕB in a time Δt. Then ΔϕB is proportional to the current through the loop.
Reason: I=−ΔϕBR)
If both asseration and reason are true and reason is the correct explanation of assertion.
If both asseration and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If assertion is false but reason is true.
The correct Answer is:A
I=−ΔϕBR
As R is constant, IpropDeltaphi_(B).
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - AIPMTNEET Questions27videos
ELECTROMAGNETIC INDUCTION
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - AIIMS Questions27videos
ELECTROMAGNETIC INDUCTION
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Problems On Mixed Concepts37videos
ELECTROMAGNETIC INDUCTION
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test29videos
ELECTRIC POTENTIAL & CAPACITANCE
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test30videos
ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM
Similar Questions
The magnetic field through a circular loop of wire 12 cm in radius and 8.5 ohm resistance, changes with time as shown in Fig. The magnetic field is perpendicular to the plane of the loop. Calculate the induced current in the loop and plot is as a function of time.
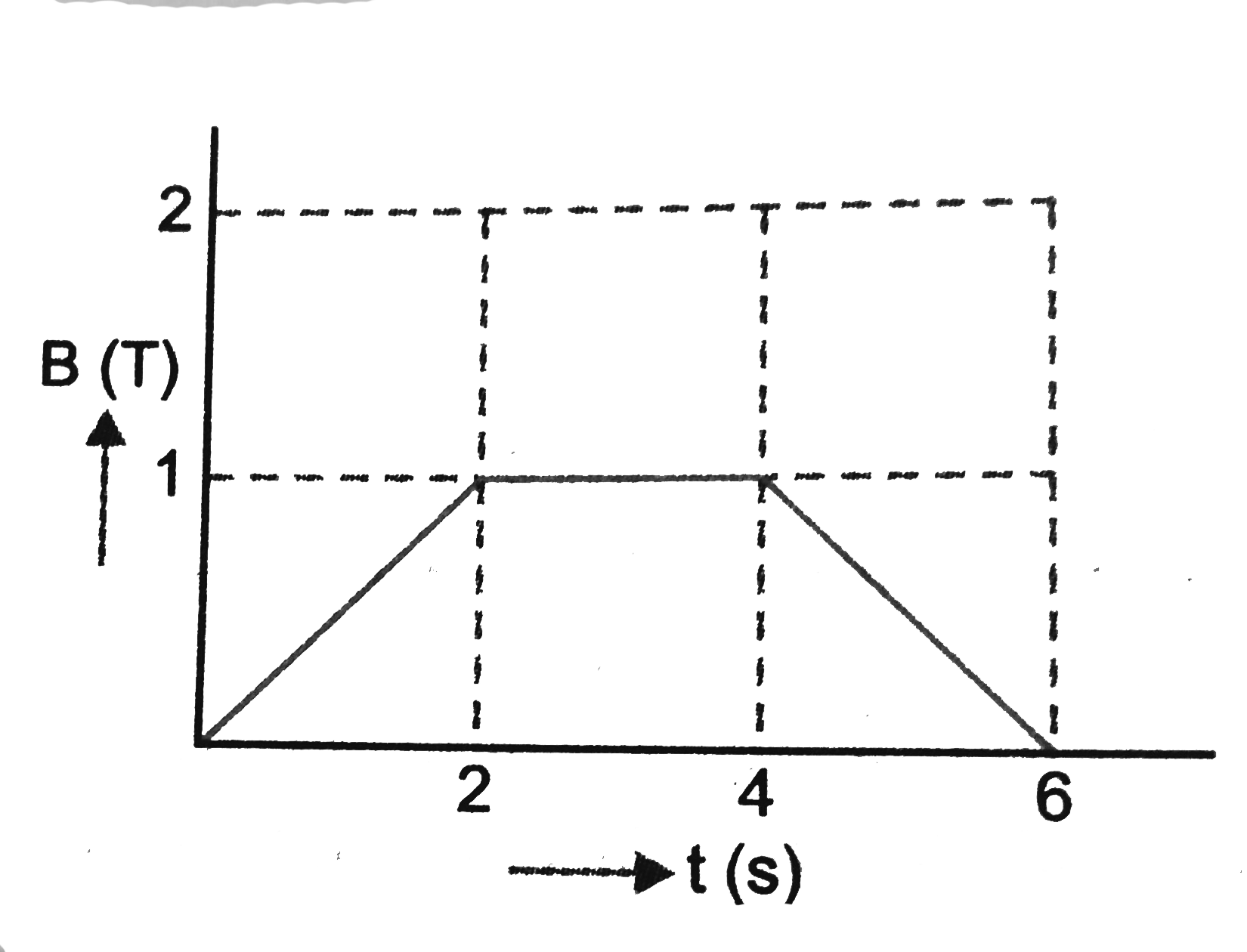 View Solution
View SolutionA uniform magnetic field B=B0tˆi in a region exists. A circular conducting loop of radius r and resistance R is placed with its plane in yz-plane. Determine the current through the loop and sense of the current.
View Solution
Knowledge Check
- Question 1 - Select One
STATEMENT-1: The magnetic flux through a loop of conducting wire of a fixed resistance changes by ΔϕB in a ime Δt. Then ΔϕB is propotional to the current through the loop.
STATEMENT-2: I=−ΔϕBRAStatement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1.BStatement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True. - Question 2 - Select One
The magnetic flux through a circuit of resistance R changes by an amount Δϕ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represent by
AQ=1r.ΔϕΔtBQ=ΔϕRCQ=ΔϕΔtDQ=(R).ΔϕΔt - Question 3 - Select One
The magnetic flux through a stationary loop with resistance R varies during interval of time T as ϕ = at (T – t). The heat generated during this time neglecting the inductance of loop will be
Aa2T33RBa2T23RCa2T3RDa2T3R
A square loop a, b, c, d of a conducting wire has been changed into a rectangular loop a′, b′, c′, d′ as shown in figure. What is the direction of induced current in the loop?
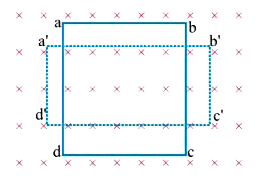 View Solution
View SolutionAt the Earth's equator, B is horizontal and to the north, with a magnitude of approximately 7×10−5T. (a) What is the magnetic flux through a loop of radius 0.1 m, lying flat on the ground? (b) If the same loop is balanced on its edge such that its axis points northwest, what is the magnetic flux through the loop? (c) If the loop is now rotated such that its axis points north, what is the magnetic flux through the loop? (d) If the loop is now rotated such that its axis points west, what is the magnetic flux through the loop?
View SolutionThere exists a uniform magnetic field ¯¯¯B=B0t¯k in a region. A circular conducting loop of radius r and resistance R is placed with its plane in x-y plane. Determine the current through the loop and sense of the current.
View SolutionA magnetic flux through a stationary loop with a resistance R varies during the time interval τ as ϕ=at(τ−t). Find the amount of the generated in the loop during that time
View SolutionA loop of flexible conducting wire of length l lies in magnetic field B which is normal to the plane of loop. A current l is passed through the loop. The tension developed in the wire to open up is
View Solution

