Asserion: Magnitude of the resultant of two vectors may be less than the magnitude of either vector.
Reason: The resultant of two vectors is obtained by means of law of parallelogram of Vectors.
The correct Answer is:B
To analyze the assertion and reason provided in the question, we will break it down step by step.
Step 1: Understanding the Assertion
The assertion states that "the magnitude of the resultant of two vectors may be less than the magnitude of either vector."
- Explanation: This means that when you add two vectors, the resultant vector (the vector that represents the combined effect of the two vectors) can sometimes have a smaller magnitude than either of the individual vectors.
Step 2: Analyzing with Examples
To understand this better, let's consider two vectors, A and B.
- Case 1: If both vectors are in the same direction, the resultant vector (C = A + B) will be greater than both A and B.
- Case 2: If the two vectors are in opposite directions, the resultant can be less than the magnitude of either vector. For example, if A = 5 units to the right and B = 3 units to the left, the resultant C = A - B = 5 - 3 = 2 units to the right, which is less than the magnitude of A.
Step 3: Conclusion on the Assertion
From our analysis, we can conclude that the assertion is true because there are scenarios (like Case 2) where the resultant can indeed be less than either of the vectors.
Step 4: Understanding the Reason
The reason states that "the resultant of two vectors is obtained by means of the law of parallelogram of vectors."
- Explanation: The law of parallelogram states that if two vectors are represented as two sides of a parallelogram, then the diagonal of the parallelogram represents the resultant vector.
Step 5: Analyzing the Reason
While the reason is correct in stating how to find the resultant vector, it does not specifically explain why the resultant can be less than either vector.
Step 6: Conclusion on the Reason
Thus, the reason is true, but it does not provide an explanation for the assertion.
Final Conclusion
Both the assertion and the reason are true, but the reason does not explain the assertion.
Summary
- Assertion: True
- Reason: True, but does not explain the assertion.
The assertion states that "the magnitude of the resultant of two vectors may be less than the magnitude of either vector."
To understand this better, let's consider two vectors, A and B.
- Case 2: If the two vectors are in opposite directions, the resultant can be less than the magnitude of either vector. For example, if A = 5 units to the right and B = 3 units to the left, the resultant C = A - B = 5 - 3 = 2 units to the right, which is less than the magnitude of A.
From our analysis, we can conclude that the assertion is true because there are scenarios (like Case 2) where the resultant can indeed be less than either of the vectors.
The reason states that "the resultant of two vectors is obtained by means of the law of parallelogram of vectors."
While the reason is correct in stating how to find the resultant vector, it does not specifically explain why the resultant can be less than either vector.
Thus, the reason is true, but it does not provide an explanation for the assertion.
Both the assertion and the reason are true, but the reason does not explain the assertion.
- Assertion: True
- Reason: True, but does not explain the assertion.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Scalars And Vectors5videos
MOTION IN A PLANE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Addition And Subtraction Of Vectors - Graphical Method6videos
MOTION IN A PLANE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - EXEMPLER PROBLEMS9videos
MOTION IN A PLANE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason15videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar6videos
MOTION IN A STRAIGHT LINE
Similar Questions
Knowledge Check
- Question 1 - Select One
If the sum of two unit vectors is a unit vector, then the magnitude of their difference is :
A√3B√2C√5D1√2
Find the magnitude and direction of the resultant of given vectors
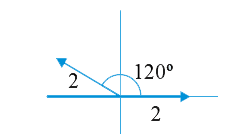 View Solution
View SolutionIf magnitude of the resultant of two vectors equal of magnitude, is equal to the magnitude of either of the vectors, what is the angle between them ?
View SolutionMagnitude of resultant of two vectors →P and →Q is equal to magnitude of →P . Find the angle between →Q and resultant of →2P and →Q .
View SolutionThe magnitude of the vectors product of two vectors →Aand→B may be
View SolutionIf the sum of two unit vectors is a unit vector, then magnitude of difference is-
View SolutionThe magnitude of the vector product of two vectors →A and →B may not be:
View SolutionThe magnitude of the vectors product of two vectors ∣∣→A∣∣and∣∣→B∣∣ may be
View Solution

