Assertion: A ball is released on a rough ground in the condition shown in figure. it will start pure rolling after some time towards left side.
Reason: Friction will convert the pure rotational motion of the ball into pure rolling

Both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
Both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
Assertion is true, but the reaction is false.
Assertion is false but the reason is true.

Slips is towrads right. So maximum friction will act towards left which will convert this slip into pure rolling.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective
30 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.11
2 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A small spherical ball is released from a point at a height h on a rough track shown in figure. Assuming that it does not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.

View SolutionAssertion: A ring is rolling without slipping on a rough ground. It strikes elastically with a smooth wall as shown in figure. Ring will stop after some time while travelling in opposite direction.
Reason: After impact net angular momentum about an axis passing through bottommost point and perpendicular to plane of paper is zero.
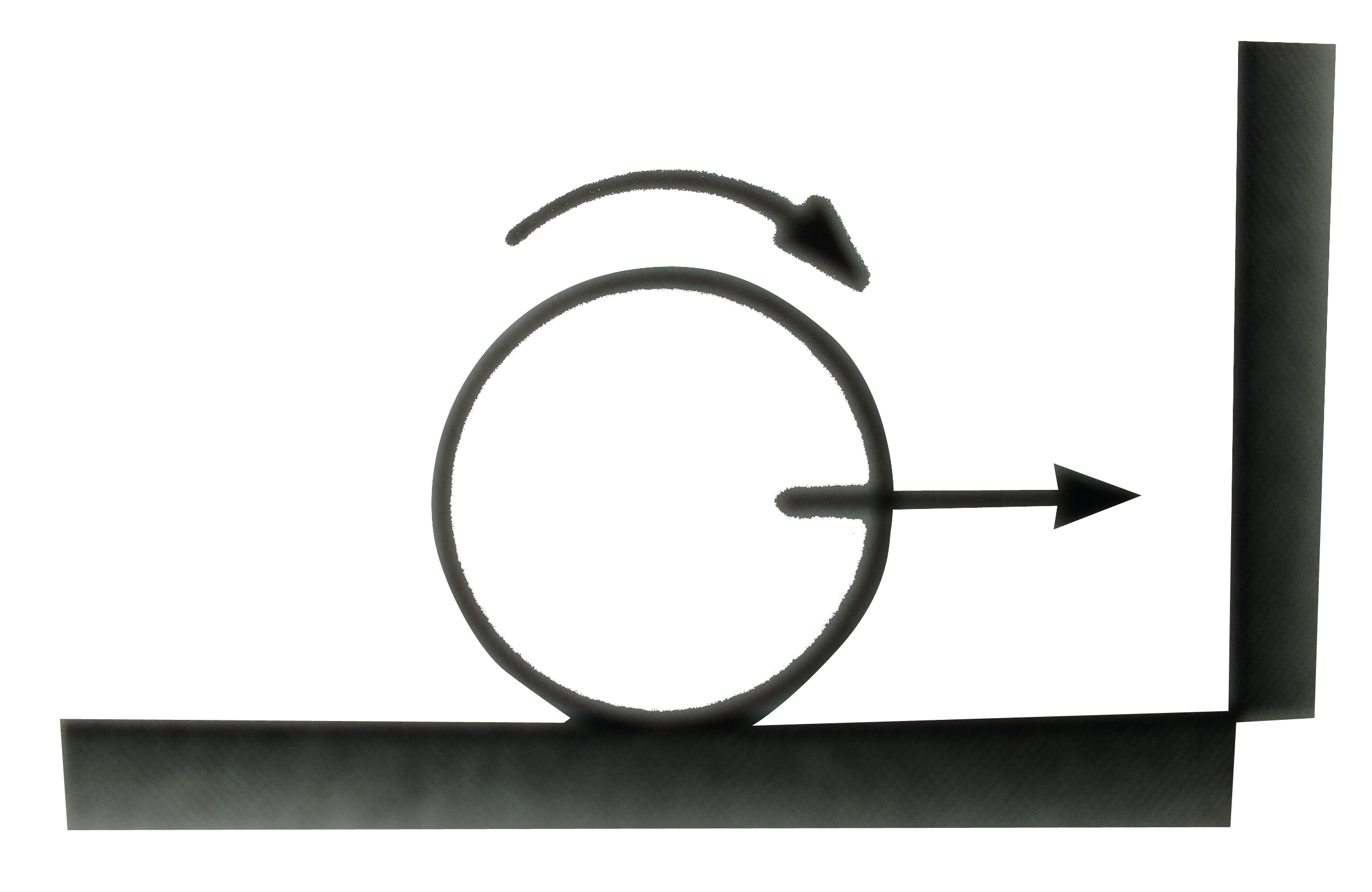
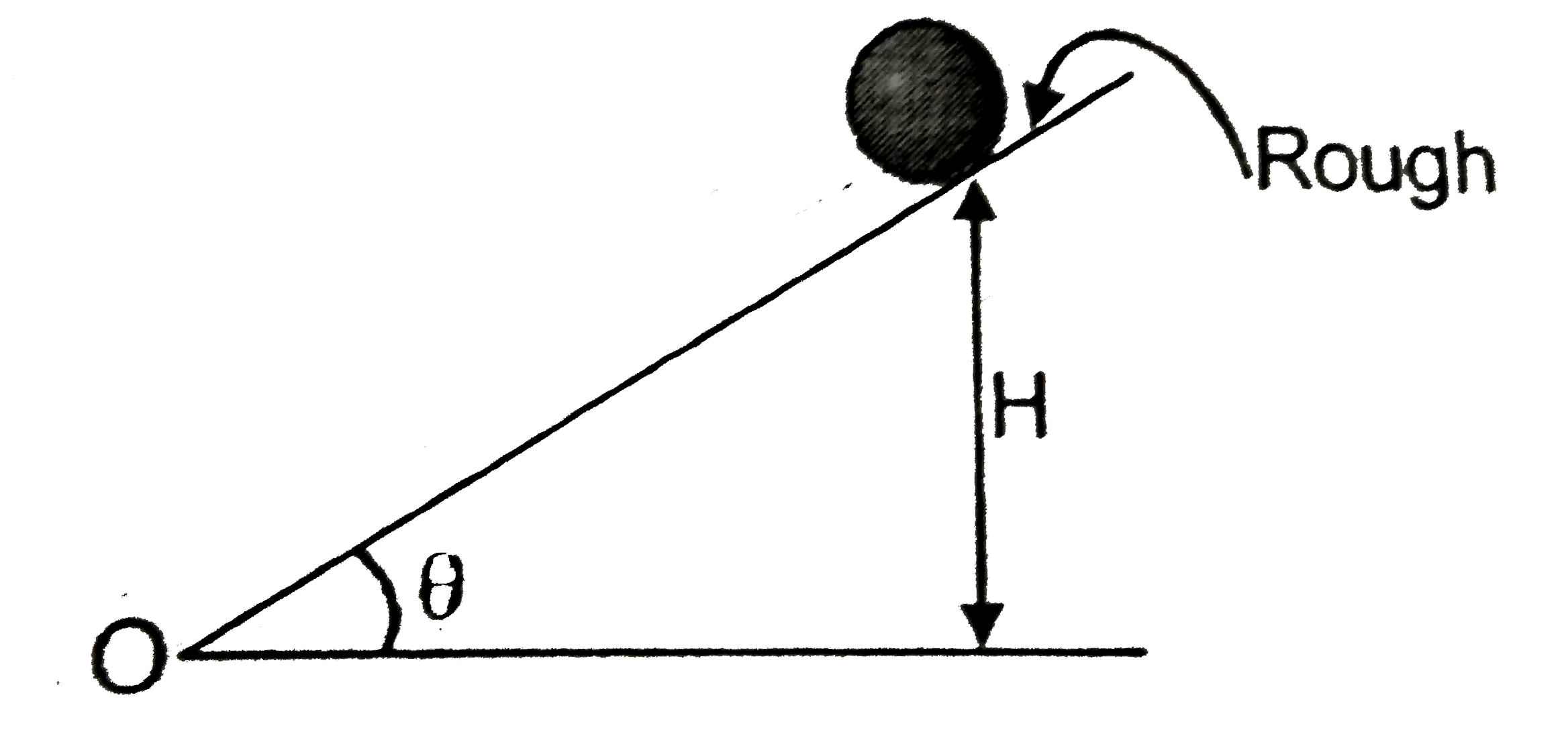
View SolutionA solid ball of mass 'm' is released on a rough fixed inclined plane from height H. The ball will perform pure rolling on the inclined plane. Then
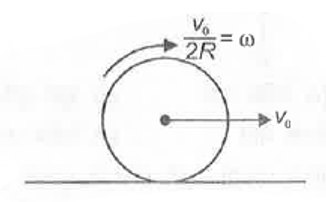
View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
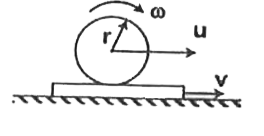
View SolutionA uniform disc is having a pure rolling motion on a moving plank as shown in the figure. Choose the correct option among the following .
View SolutionA conducting straight wire PQ of length l is fixed along as diameter of a non conducting ring as shown in the figure. The ring is given a pure rolling motion as shown. Field B is horizontal in direction and perpendicular to the plane of ring. The magnitude of induced EMF in the wire PQ at the position shown in figure will be

View SolutionA conducnting straight wire PQ of length l is fixed along as diameter of a non conducting ring as shown in the figure. The ring is given a pure rolling motion on as horizontal masgnetic field B in horizontal direction perpendicular to the plane of ring. The magnitude of induced emf in the wire PQ at the position shown in figure will be

View SolutionA solid spherical ball of mass m is released from the topmost point of the shown semi - spherical shell. The track is sufficiently rough to enablle to enable pure rolling motion. The normal force between the ball and the shell at the lowest position is
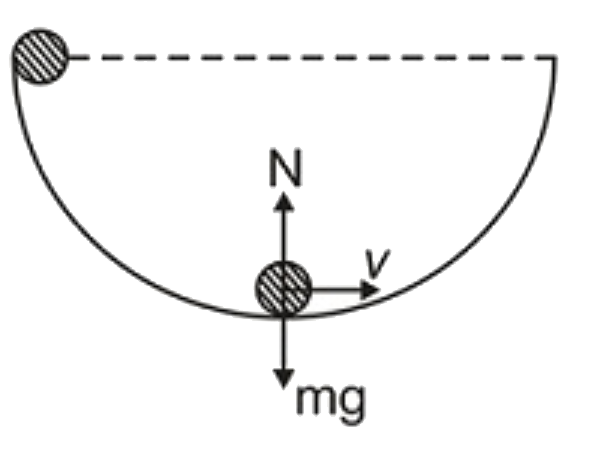
View Solution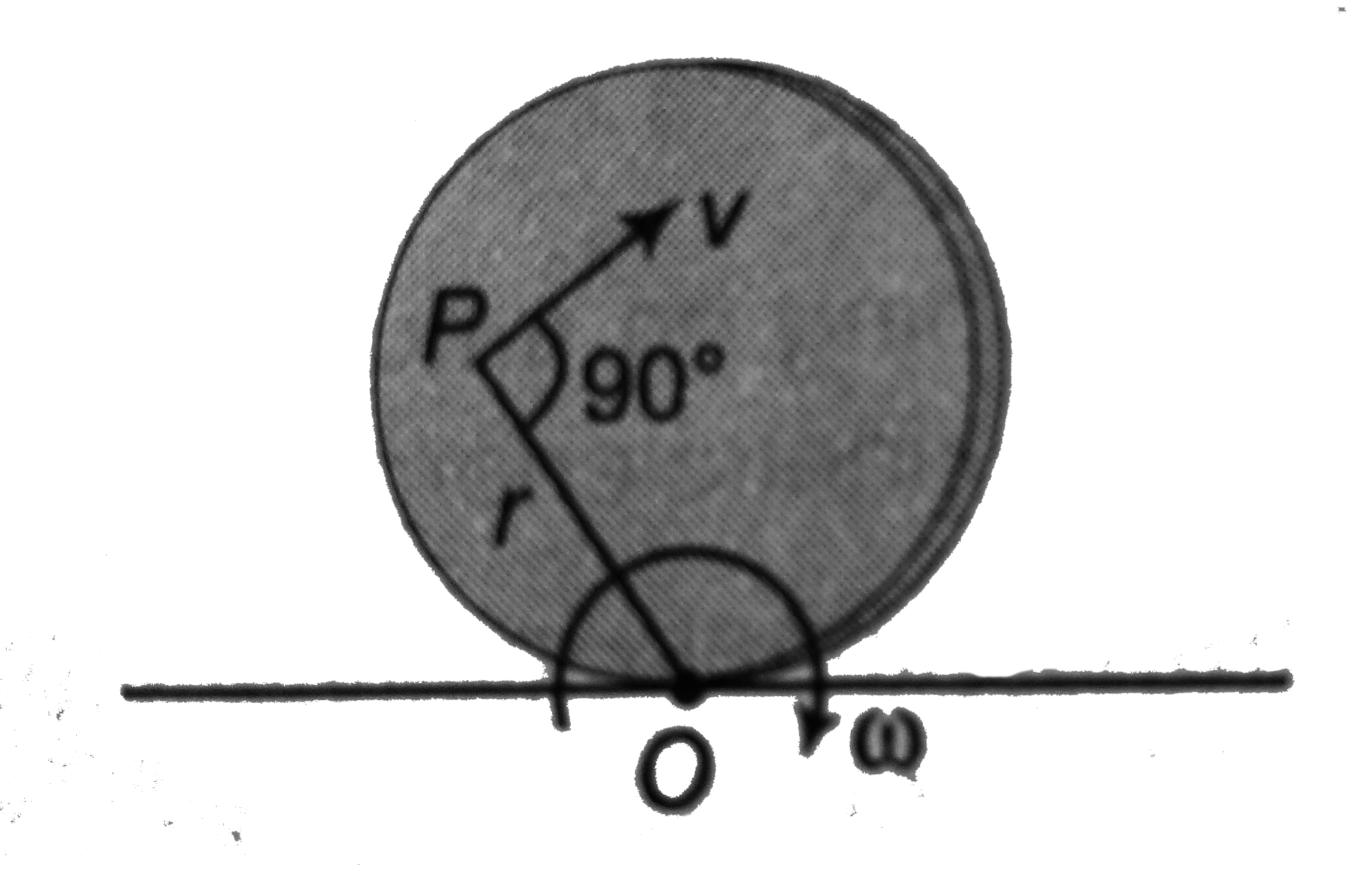
Using the concept of instantaneous axis of rotation. Find speed of particle P as shown in figure, under pure rolling condition.
View Solution
