Assertion : A body of mass 4 kg has an initial velocity 5ˆims−1. It is subjected to a force of 4ˆjN. The displacement of body from origin after 4 s will be 21.5m.
Reason : The equation v=u+at can be applied to obtain v if a is constant.
If both Assertion and Reason are correct and Reason is the correct explanation of assertion.
If both Assertion and Reason are correct but Reason in not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:B
To solve the problem step by step, we will analyze the assertion and reason provided in the question.
Step 1: Identify Given Information
- Mass of the body, m=4kg
- Initial velocity, u=5^im/s
- Force acting on the body, F=4^jN
- Time, t=4s
Step 2: Calculate Acceleration
Using Newton's second law, the acceleration a can be calculated as:
a=Fm
Substituting the values:
a=4^j4=1^jm/s2
Step 3: Calculate Displacement
The formula for displacement s when initial velocity, acceleration, and time are known is:
s=ut+12at2
Substituting the known values:
s=(5^i)(4)+12(1^j)(42)
Calculating each term:
s=20^i+12(1^j)(16)=20^i+8^j
Thus, the displacement vector is:
s=20^i+8^jm
Step 4: Calculate Magnitude of Displacement
The magnitude of displacement s can be calculated using the Pythagorean theorem:
s=√(20)2+(8)2=√400+64=√464≈21.5m
Step 5: Conclusion on Assertion
The assertion states that the displacement of the body from the origin after 4 seconds will be 21.5m. From our calculations, this is indeed true.
Step 6: Conclusion on Reason
The reason states that the equation v=u+at can be applied to obtain v if a is constant. This is also true, but it does not directly explain the assertion regarding displacement. Therefore, while both the assertion and reason are true, the reason does not correctly explain the assertion.
Final Answer
- Assertion: True
- Reason: True, but not the correct explanation for the assertion.
- Mass of the body, m=4kg
- Initial velocity, u=5^im/s
- Force acting on the body, F=4^jN
- Time, t=4s
Using Newton's second law, the acceleration a can be calculated as:
a=Fm
Substituting the values:
a=4^j4=1^jm/s2
The formula for displacement s when initial velocity, acceleration, and time are known is:
s=ut+12at2
Substituting the known values:
s=(5^i)(4)+12(1^j)(42)
Calculating each term:
s=20^i+12(1^j)(16)=20^i+8^j
Thus, the displacement vector is:
s=20^i+8^jm
The magnitude of displacement s can be calculated using the Pythagorean theorem:
s=√(20)2+(8)2=√400+64=√464≈21.5m
The assertion states that the displacement of the body from the origin after 4 seconds will be 21.5m. From our calculations, this is indeed true.
The reason states that the equation v=u+at can be applied to obtain v if a is constant. This is also true, but it does not directly explain the assertion regarding displacement. Therefore, while both the assertion and reason are true, the reason does not correctly explain the assertion.
- Assertion: True
- Reason: True, but not the correct explanation for the assertion.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Mathch the columns)
6 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (A) Taking it together
75 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
A body mass 2kg has an initial velocity of 3 metre//sec along OE and it is subject to a force of 4N in a direction perpendicular to OE. The distance of body from O after 4 sec will be:
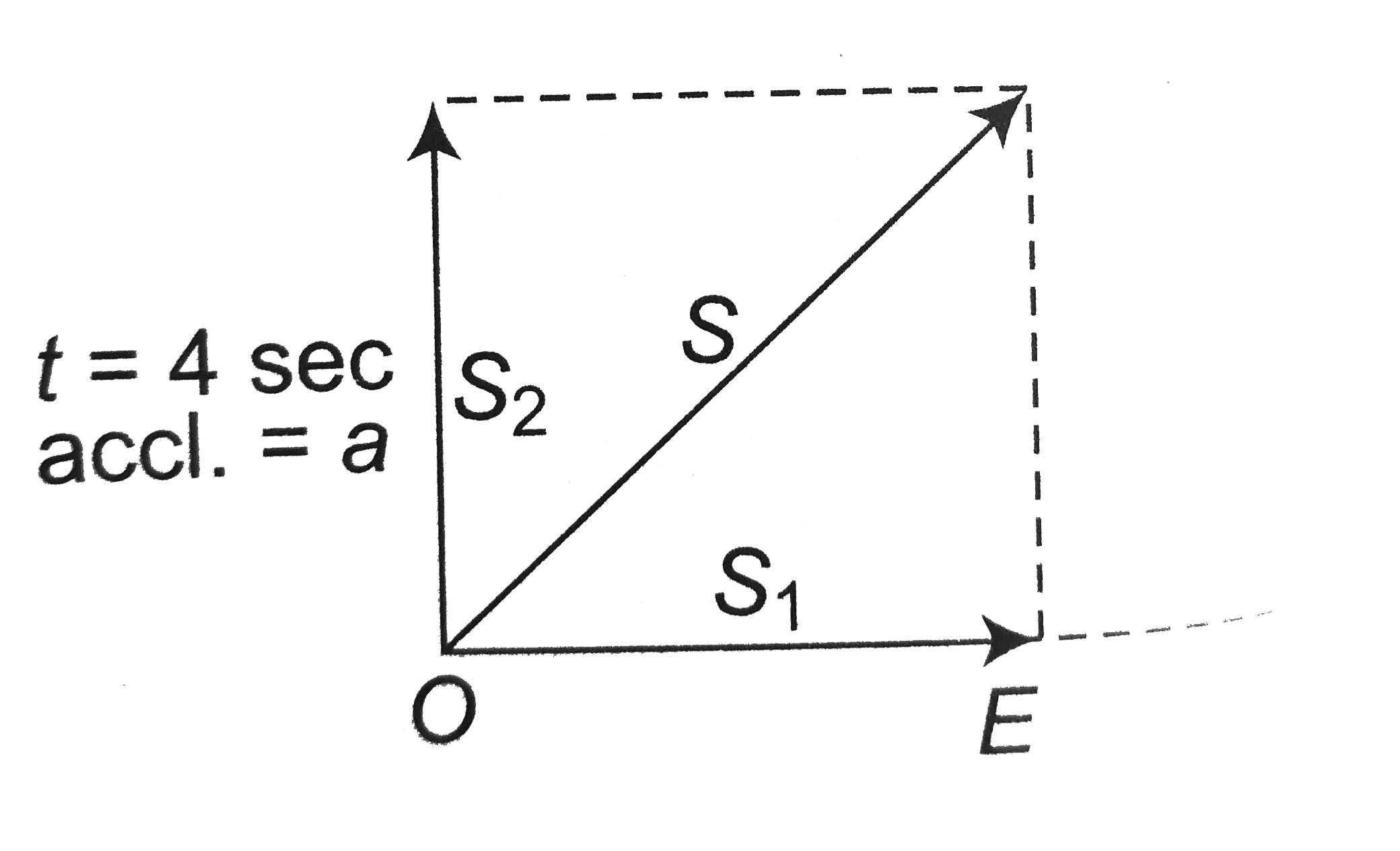
View SolutionA body mass 2kg has an initial velocity of 3 metre//sec along OE and it is subject to a force of 4N in a direction perpendicular to OE. The distance of body from O after 4 sec will be:

View SolutionA body of mass 2kg has an initial velocity of 3ms−1 along OE and it is subjected to a force of 4N in OF direction perpendicular to OE. Find the distance of the body from O after 4s.
 .
.
View SolutionA body of mass 14kg moving with velocity 12m/s is stopped by applying a force of 0.6 N. Then impulse is :-
View SolutionA body of mass 5 kg initially at rest is subjected to a force of 20 N. What is the kinetic energy acquired by the body at the end of 10 s?
View SolutionA body of mass 1 kg is moving with velocity 30ms−1 due north. It is acted on by a force of 10 N due east for 4 seconds. Find the velocity of the body after the force ceases to act.
View SolutionA particle has an initial velocity of 3ˆi+4ˆj and an acceleration of 0.4ˆi+0.3ˆj. Its speed after 10s is :
View SolutionA particle has an initial velocity of 3ˆi+4ˆj and an acceleration of 0.4ˆi+0.3ˆj. Its speed after 10s is :
View SolutionAn object of mass 2 kg at rest at origin starts moving under the action of a force
→F=(3t2ˆi+4tˆj)N The velocity of the object at t = 2 s will be -
View SolutionA body of mass 5 kg statrs from the origin with an initial velocity →u=(30ˆi+40ˆj)ms−1. If a constant force (−6ˆi−5ˆj)N acts on the body, the time in which the y component of the velocity becomes zero is
View Solution
