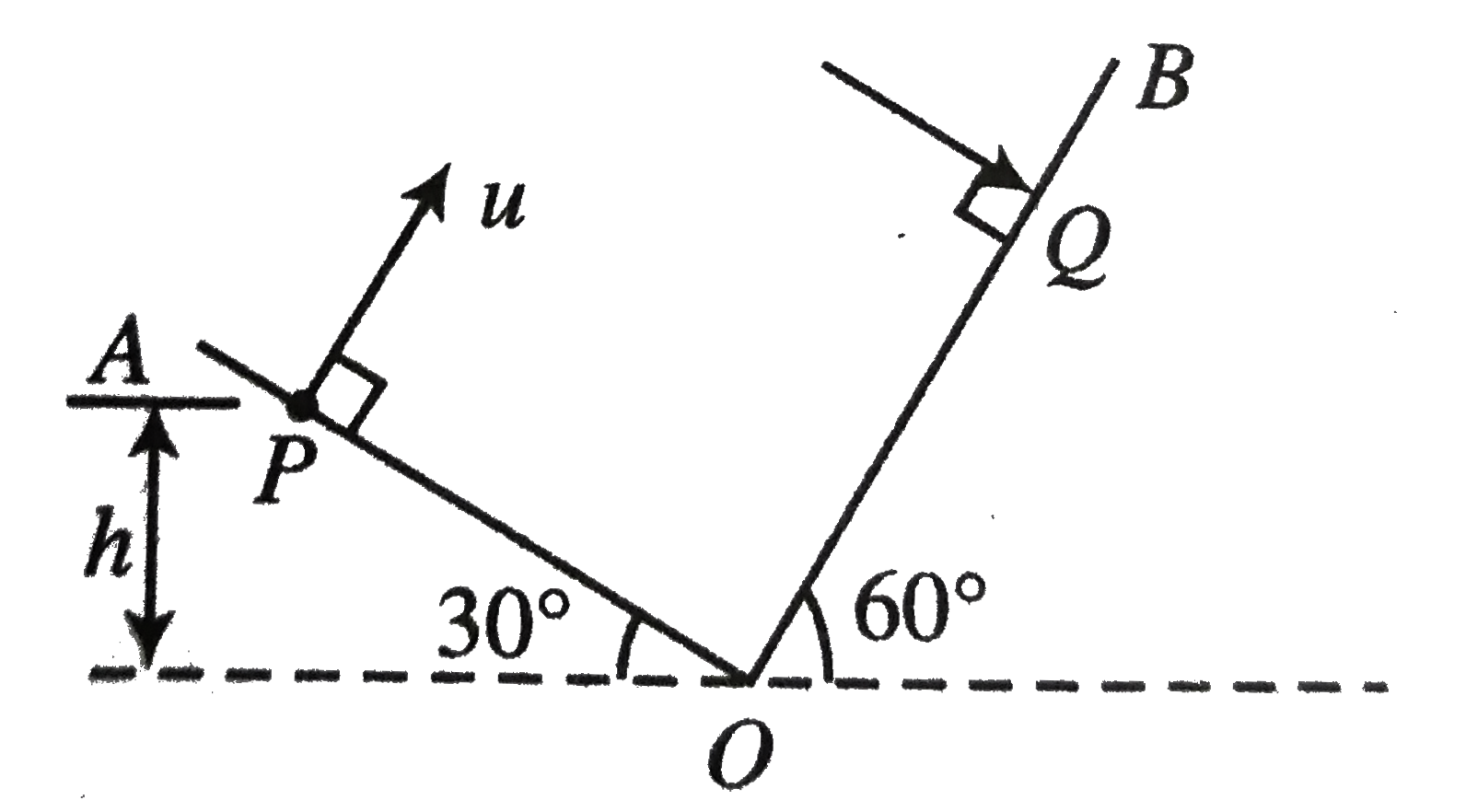
Two inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.

If α=30∘,β=30∘ the time of flight from P to Q is
tan−1[P2+PQ+Q2PQ]
tan−1[P2+Q2−PQPQ]
tan−1[P2+Q22PQ]
sin−1[P2+Q2+PQ2PQ]
The correct Answer is:A
The equation of trajectory.
y=xtanα[1−xR] gives
Q=Ptanθ[1−PR] ...(i)
and P=Qtanθ[1−QR] ......(ii)
On dividing we get, Q2P2=[1−P/R][1−Q/R]
1R[P3−Q3]=P2−Q2
R=P3−Q3P2−Q2=P+PQ+Q2P+Q
Now, QP=tanθ[1−P(P+Q)P2+PQ+Q2]
=tanθ[P2+PQ+Q2−P2−PQP2+PQ+Q2]
⇒tanθ=P2+Q2+PQPQ
⇒θ=tan−1[P2+PQ+Q2PQ]
Topper's Solved these Questions
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - C. Medical entrances gallery
1 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
Similar Questions
Two inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.
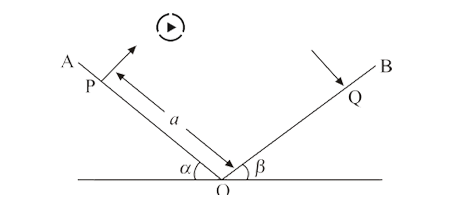
The path of the particle from P to Q is
View SolutionTwo inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.
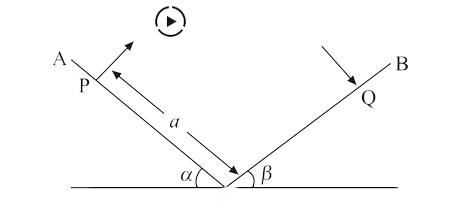
If α=30∘,β=30∘ and a = 4.9 m, the initial velocity of projection is
View SolutionTwo inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.

If α=30∘,β=30∘ and a = 4.9 m, the initial velocity of projection is
View SolutionTwo inclined planes OA and OB having inclinations 30∘ and 60∘ with the horizontal respectively intersect each other at O, as shown in figure. A particle is projected from point P with velocity u=10√3m/s along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicular at Q. Calculate.
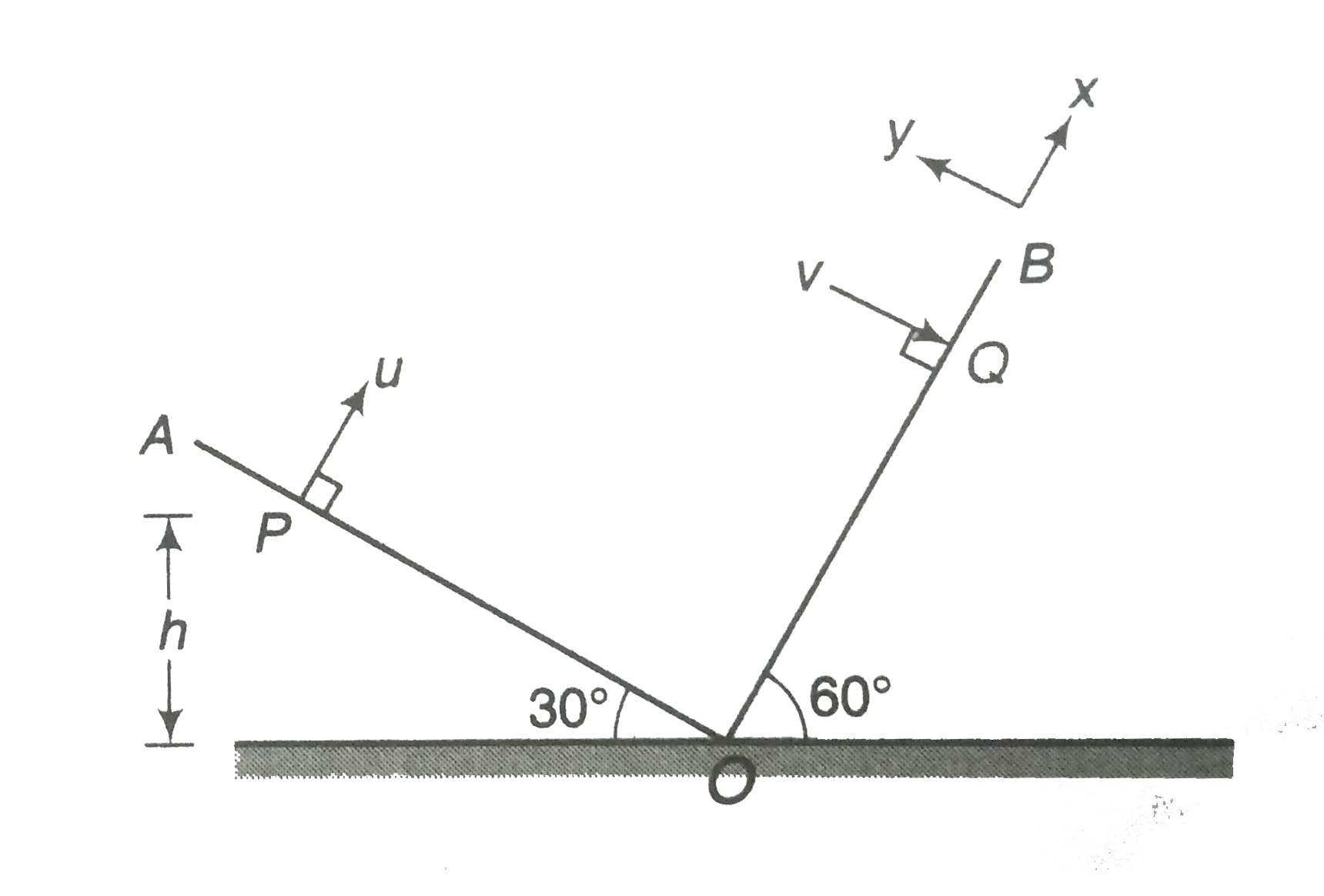
(a) time of flight,
(b) velocity with which the particle strikes the plane OB,
(c) height h of point P from point O,
(d) distance PQ. (Take g=10m/s2)
View SolutionTwo inclined planes OA and OB having inclination (with horizontal) 30∘and60∘, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity u=10√3ms−1 along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate
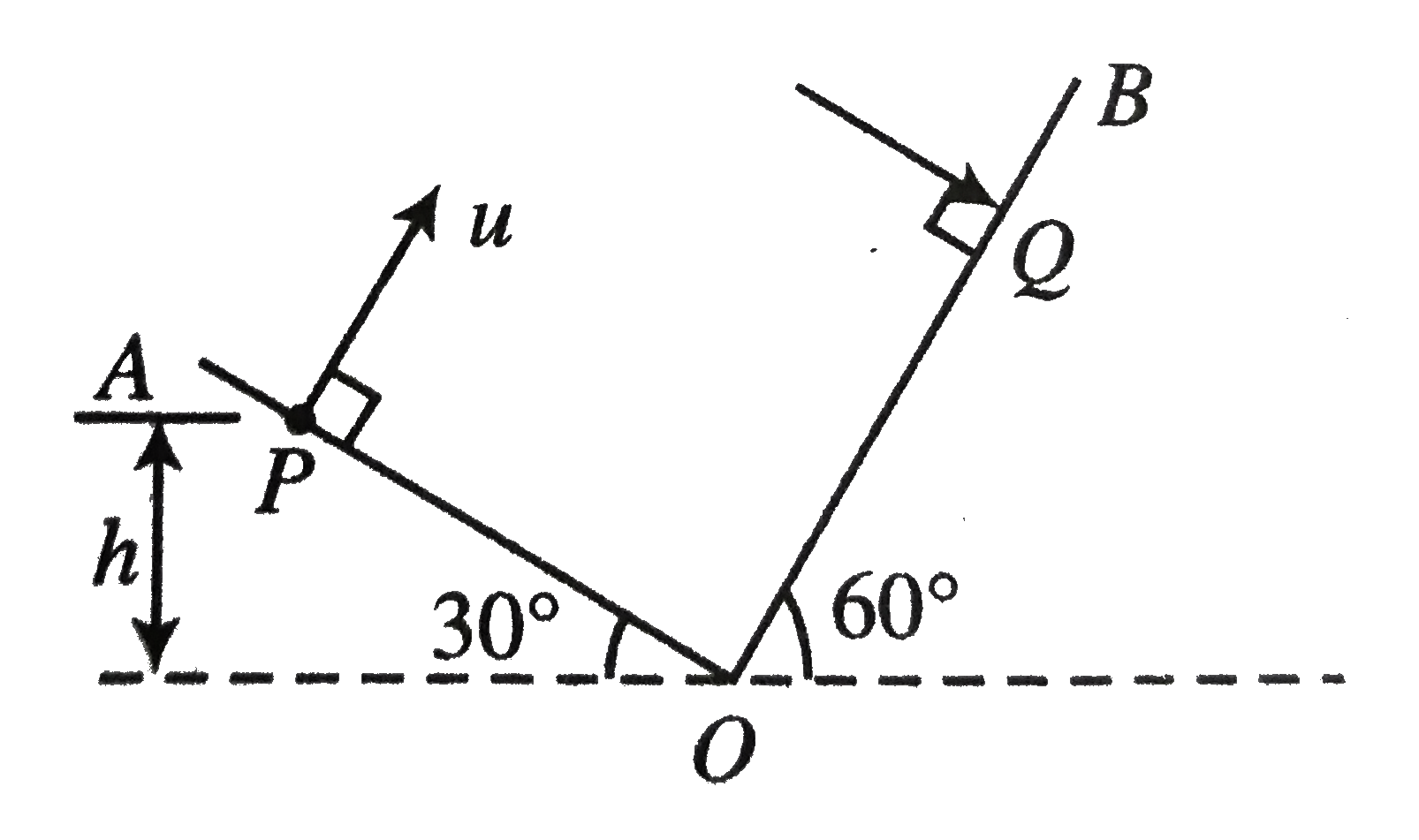
The vertical height h of P from O,
View SolutionTwo inclined planes OA and OB having inclination (with horizontal) 30∘ and 60∘(with horizontal), respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity u=10√3ms−1 along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate
The maximum height attained by the particle (from the line O)
View SolutionTwo inclined planes OA and OB having inclination (with horizontal) 30∘ and 60∘, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity u=10(√3)ms−1 along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate

The velocity with which particle strikes the plane OB,
View SolutionA stone must be projected horizontally from a point P, which is h meter above the foot of a plane inclined at an angle θ with horizontal as shown in figure . Calculate the velocity v of the stone so that in may hit the incline plane perpendiculary.

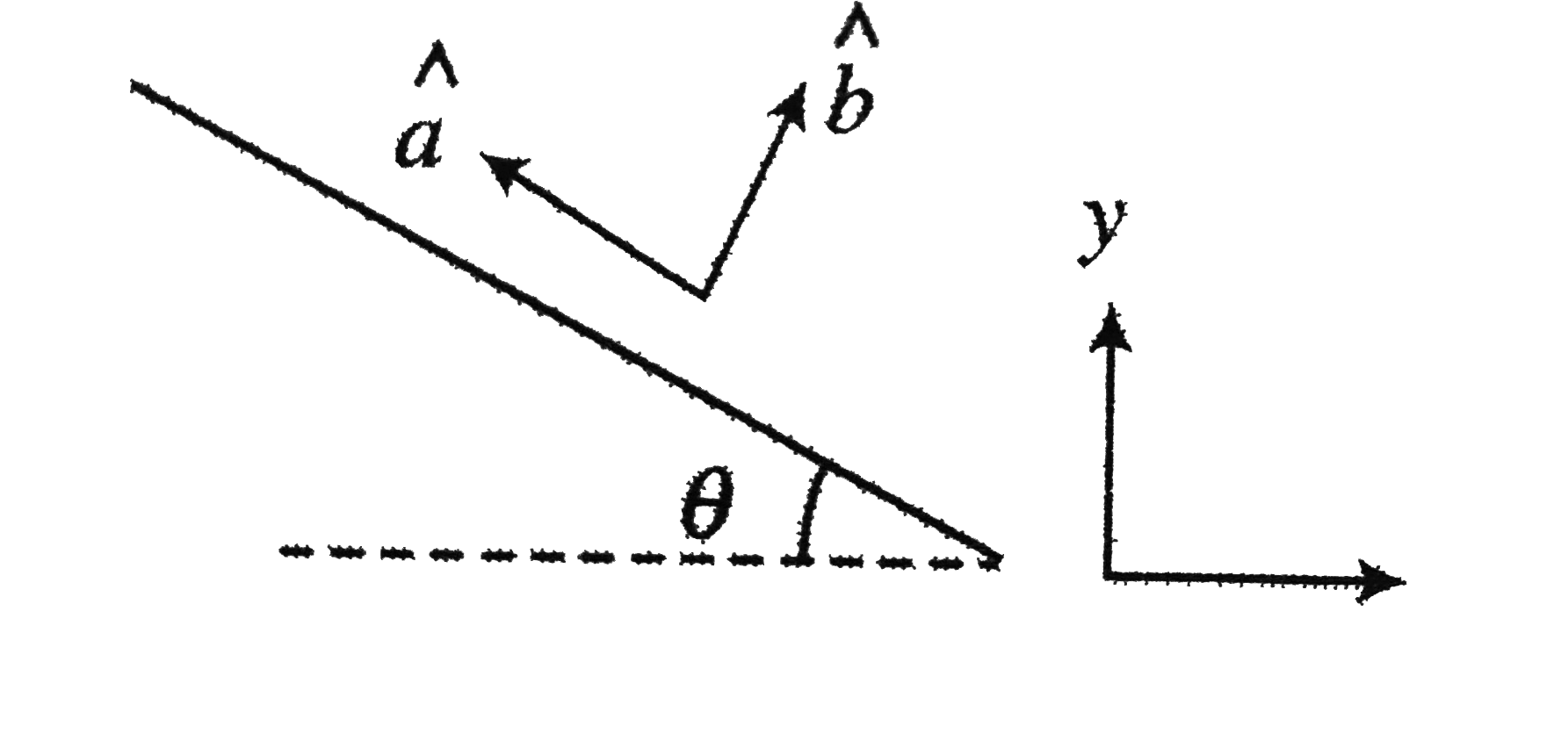
View SolutionAn inclined plane is inclined at θ with horizontal as shown in (figure).Write a unit vector in the direction parallel (ˆa) and perpendicular (ˆb) to inclined plane,in standard xy coordinate system.
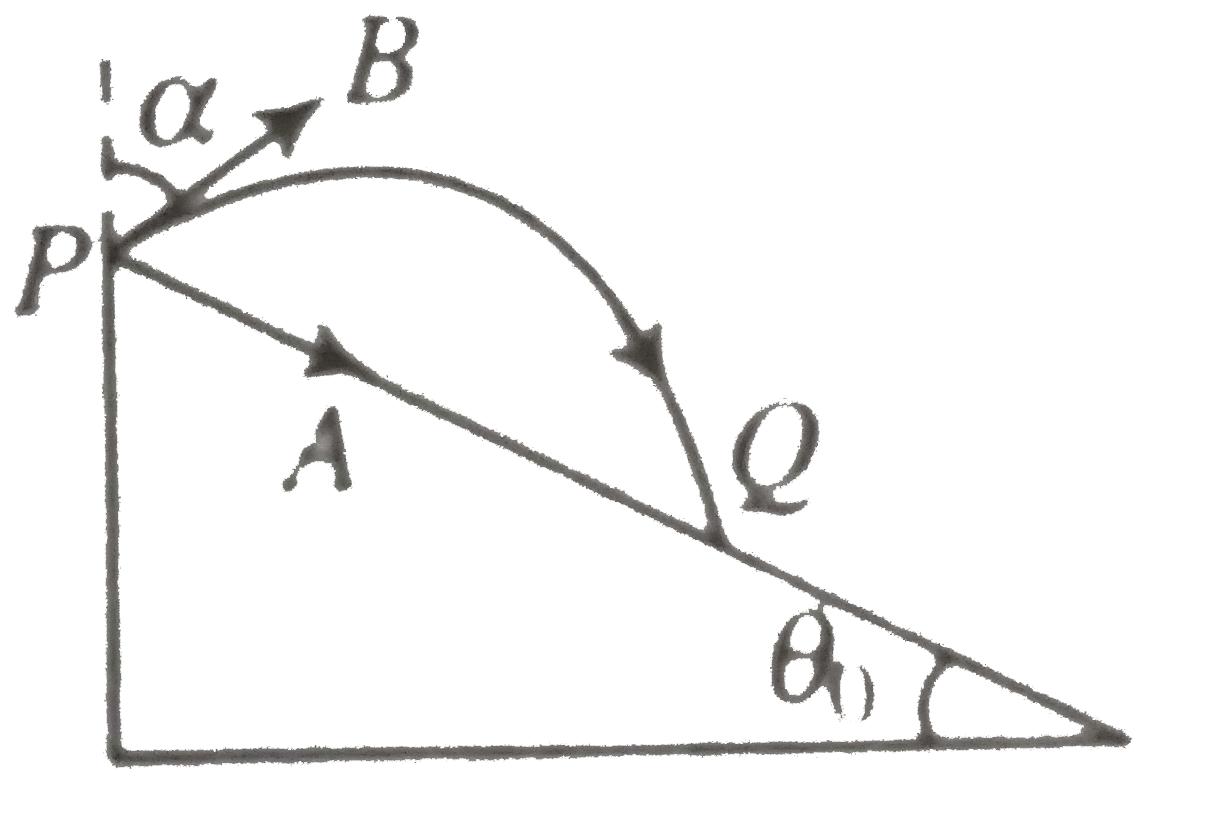
View SolutionFigure shows that particle A is projected from point P with velocity u along the plane and simultaneously another particle B with velocity v at an angle α with vertical. The particles collide at point Q on the plane. Then
View Solution
