Assertion : AC circuit derives maximum power when it is in a state of resonance.
Reason: Power factor of the circuit becomes zero in case of reasonance.
If both assertion and reason are correct and reason is a correct explanation of the assertion
If both assertion and reason are correct but reason is not the correct explanation of assertion
If assertion is correct but reason is incorrect
If assertion is inncorrect but reason is correct
The correct Answer is:C
To solve the question, we need to analyze the assertion and reason provided:
Assertion: An AC circuit derives maximum power when it is in a state of resonance.
Reason: The power factor of the circuit becomes zero in case of resonance.
1. Understanding Resonance in AC Circuits:
- In an AC circuit, resonance occurs when the inductive reactance (XL) equals the capacitive reactance (XC). This condition can be expressed as:
XL=XC
- At resonance, the impedance (Z) of the circuit is minimized and is equal to the resistance (R) of the circuit:
Z=R
2. Current at Resonance:
- The current (I) in the circuit can be expressed as:
I=VrmsZ
- Since Z=R at resonance, the current reaches its maximum value:
Imax=VrmsR
3. Power in AC Circuits:
- The average power (P) consumed in an AC circuit is given by:
P=Vrms⋅Irms⋅cosϕ
- Where ϕ is the phase difference between the voltage and current. At resonance, the power factor (cosϕ) is 1 because the voltage and current are in phase.
4. Conclusion about the Assertion:
- Since the power factor is 1 at resonance, the average power is maximized:
Pmax=Vrms⋅Irms
- Therefore, the assertion that an AC circuit derives maximum power when it is in a state of resonance is correct.
5. Analyzing the Reason:
- The reason states that the power factor becomes zero in case of resonance. This is incorrect because, as established, the power factor at resonance is actually 1 (not zero).
- Thus, the reason is incorrect.
Final Conclusion:
- The assertion is correct, but the reason is incorrect. Therefore, the correct answer is that the assertion is true, and the reason is false.
- In an AC circuit, resonance occurs when the inductive reactance (XL) equals the capacitive reactance (XC). This condition can be expressed as:
XL=XC
- At resonance, the impedance (Z) of the circuit is minimized and is equal to the resistance (R) of the circuit:
Z=R
- The current (I) in the circuit can be expressed as:
I=VrmsZ
- Since Z=R at resonance, the current reaches its maximum value:
Imax=VrmsR
- The average power (P) consumed in an AC circuit is given by:
P=Vrms⋅Irms⋅cosϕ
- Where ϕ is the phase difference between the voltage and current. At resonance, the power factor (cosϕ) is 1 because the voltage and current are in phase.
- Since the power factor is 1 at resonance, the average power is maximized:
Pmax=Vrms⋅Irms
- Therefore, the assertion that an AC circuit derives maximum power when it is in a state of resonance is correct.
- The reason states that the power factor becomes zero in case of resonance. This is incorrect because, as established, the power factor at resonance is actually 1 (not zero).
- Thus, the reason is incorrect.
- The assertion is correct, but the reason is incorrect. Therefore, the correct answer is that the assertion is true, and the reason is false.
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE INTEGER TYPE QUESTIONS
11 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE EXEMPLAR PROBLEMS (OBJECTIVE QUESTIONS ) (Multiple choice question (Type ) )
13 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE D. MULTIPLE CHOICE QUESTIONS
13 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
Similar Questions
Knowledge Check
Power factor of the circuit is –
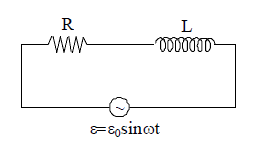 ARωLBR√R2+ω2L2CRR2+ω2L2Dnone of these
ARωLBR√R2+ω2L2CRR2+ω2L2Dnone of theseThe power factor of a circuit is
AZ/RBR/ZCR/XDX/RPower factor of the AC circuit varies between
A0 to 0.l5B0.5 to 1C0 to 1D1 to 2
The circuit shown in the diagram is in resonance. Power factor of the circuit is
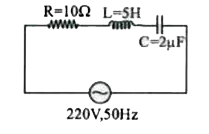
View SolutionThe power factor of L-R circuit is-
View SolutionPower consumed in an AC circuit becomes zero if
View SolutionThe power factor of the circuit shown in the figure is
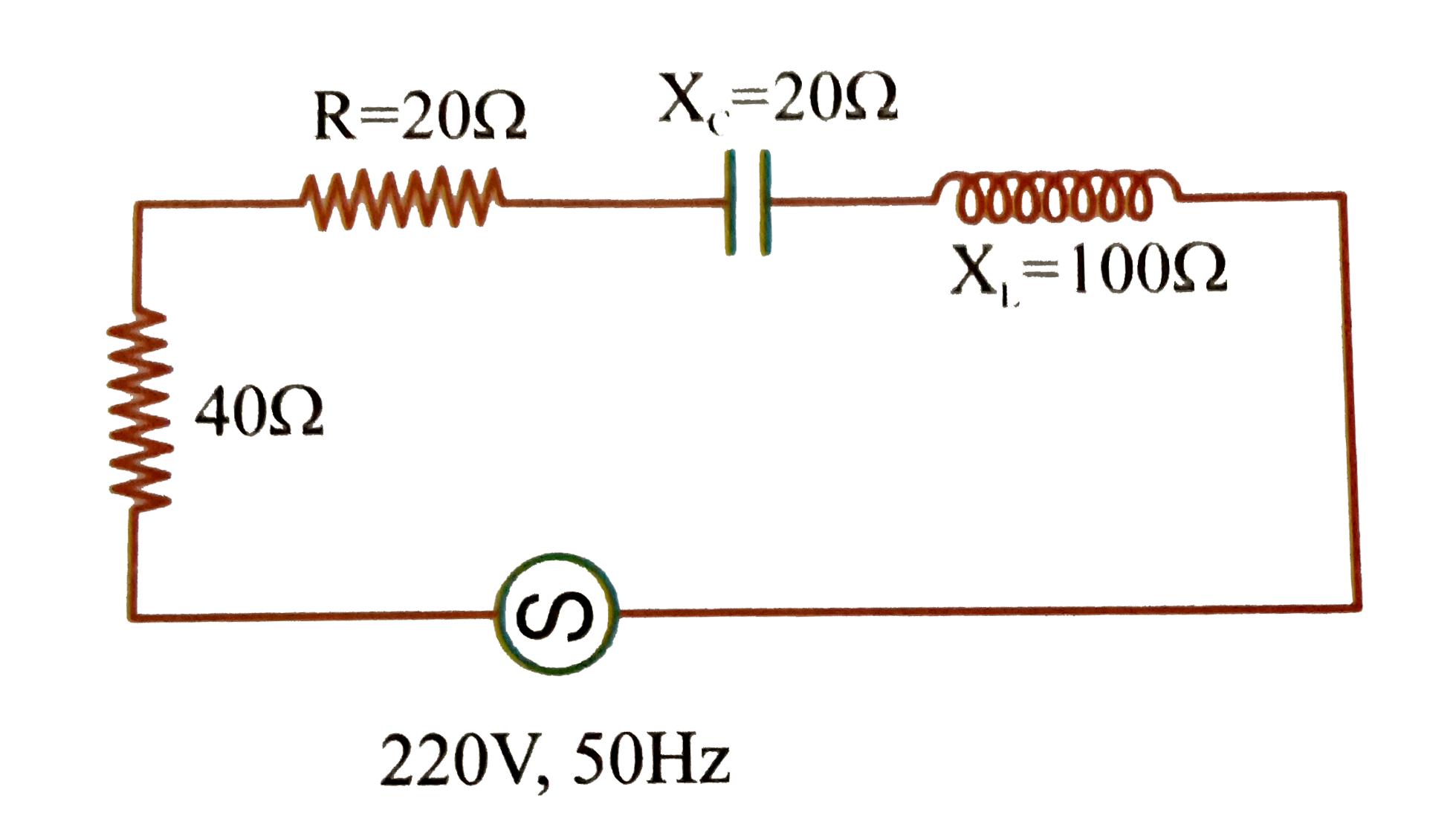
View SolutionThe power factor of the circuit as shown in figure is
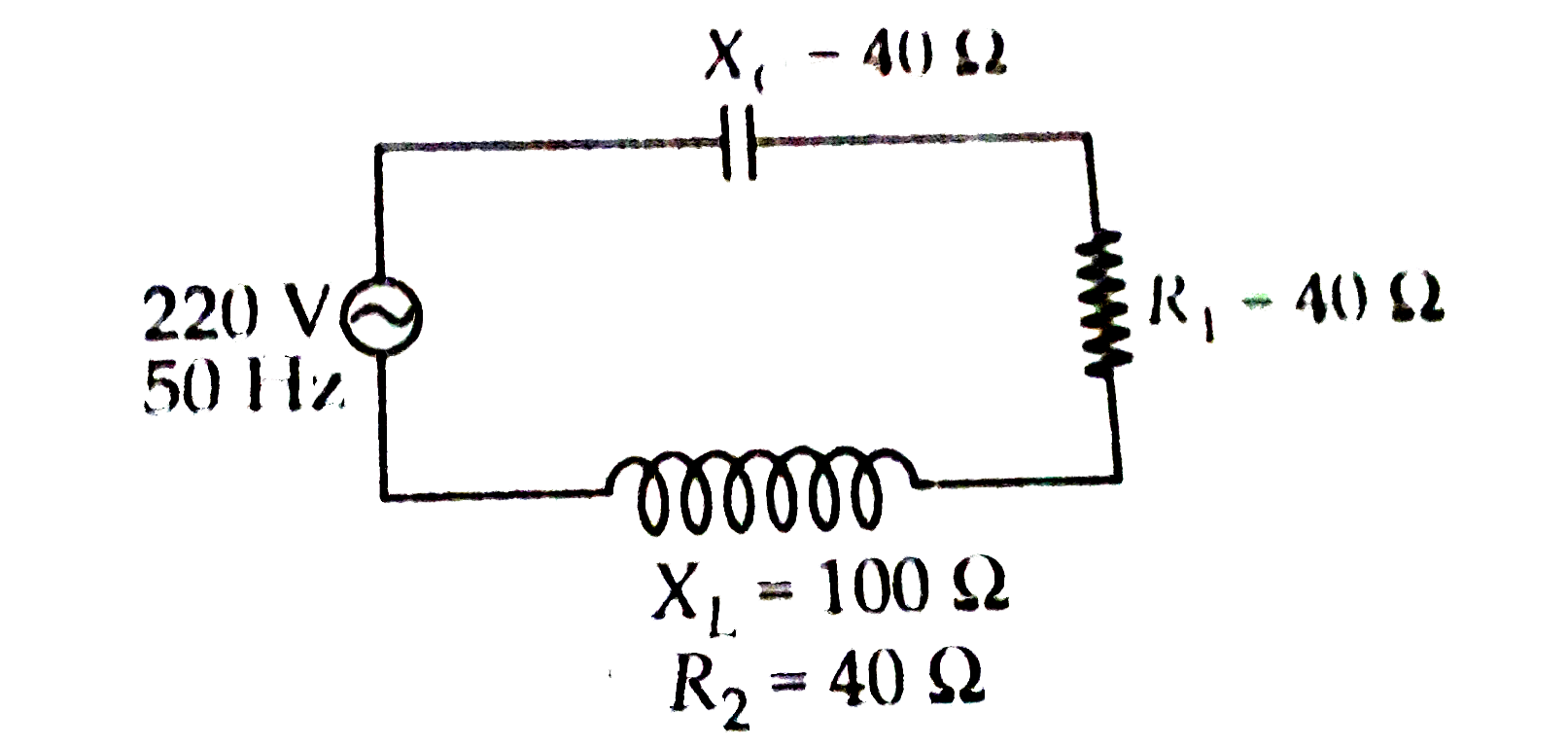
View Solution

