Assertion : If velocity - time equation of a particle moving in a straight line is quadratic in time, then displacement - time equation cannot be linear.
Reason : If displacement - time is quadratic in time, then velocity - time is linear.
If both Assertion and Reason are correct and Reason is the correct explanation of assertion.
If both Assertion and Reason are correct but Reason in not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:B
To solve the problem, we need to analyze both the assertion and the reason provided in the question.
Step 1: Understand the Assertion
The assertion states that if the velocity-time equation of a particle moving in a straight line is quadratic in time, then the displacement-time equation cannot be linear.
- Velocity-Time Equation: Let's assume the velocity v(t) is given by a quadratic equation:
v(t)=at2+bt+c
where a, b, and c are constants.
Step 2: Relate Velocity to Displacement
We know that velocity is the derivative of displacement with respect to time:
v(t)=dsdt
If v(t) is quadratic, we can integrate it to find the displacement s(t).
Step 3: Integrate the Velocity Function
Integrating the velocity function:
s(t)=∫v(t)dt=∫(at2+bt+c)dt
This gives:
s(t)=a3t3+b2t2+ct+C
where C is the constant of integration.
Step 4: Analyze the Displacement Equation
From the integration, we see that the displacement s(t) is a cubic function of time t. A cubic function cannot be linear. Therefore, the assertion is correct: if the velocity-time equation is quadratic, the displacement-time equation cannot be linear.
Step 5: Understand the Reason
The reason states that if the displacement-time equation is quadratic in time, then the velocity-time equation is linear.
- Displacement-Time Equation: Suppose s(t) is quadratic:
s(t)=At2+Bt+D
where A, B, and D are constants.
Step 6: Differentiate to Find Velocity
To find the velocity, we differentiate the displacement:
v(t)=dsdt=2At+B
This is a linear function of time t.
Conclusion
Both the assertion and the reason are correct. However, the reason does not provide a justification for the assertion. Therefore, the correct option is that the assertion is true, and the reason is also true, but the reason is not the correct explanation for the assertion.
Final Answer
The assertion is true, and the reason is true, but the reason is not the correct explanation for the assertion.
---
The assertion states that if the velocity-time equation of a particle moving in a straight line is quadratic in time, then the displacement-time equation cannot be linear.
v(t)=at2+bt+c
where a, b, and c are constants.
We know that velocity is the derivative of displacement with respect to time:
v(t)=dsdt
If v(t) is quadratic, we can integrate it to find the displacement s(t).
Integrating the velocity function:
s(t)=∫v(t)dt=∫(at2+bt+c)dt
This gives:
s(t)=a3t3+b2t2+ct+C
where C is the constant of integration.
From the integration, we see that the displacement s(t) is a cubic function of time t. A cubic function cannot be linear. Therefore, the assertion is correct: if the velocity-time equation is quadratic, the displacement-time equation cannot be linear.
The reason states that if the displacement-time equation is quadratic in time, then the velocity-time equation is linear.
s(t)=At2+Bt+D
where A, B, and D are constants.
To find the velocity, we differentiate the displacement:
v(t)=dsdt=2At+B
This is a linear function of time t.
Both the assertion and the reason are correct. However, the reason does not provide a justification for the assertion. Therefore, the correct option is that the assertion is true, and the reason is also true, but the reason is not the correct explanation for the assertion.
The assertion is true, and the reason is true, but the reason is not the correct explanation for the assertion.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Mathch the columns)
6 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (A) Taking it together
75 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
The velocity time plot for a particle moving on straight line is shown in the figure.

View SolutionThe velocity time plot for a particle moving on straight line is shown in the figure.

View SolutionDisplacement time graph of a particle moving in a straight line is a shown in figure.
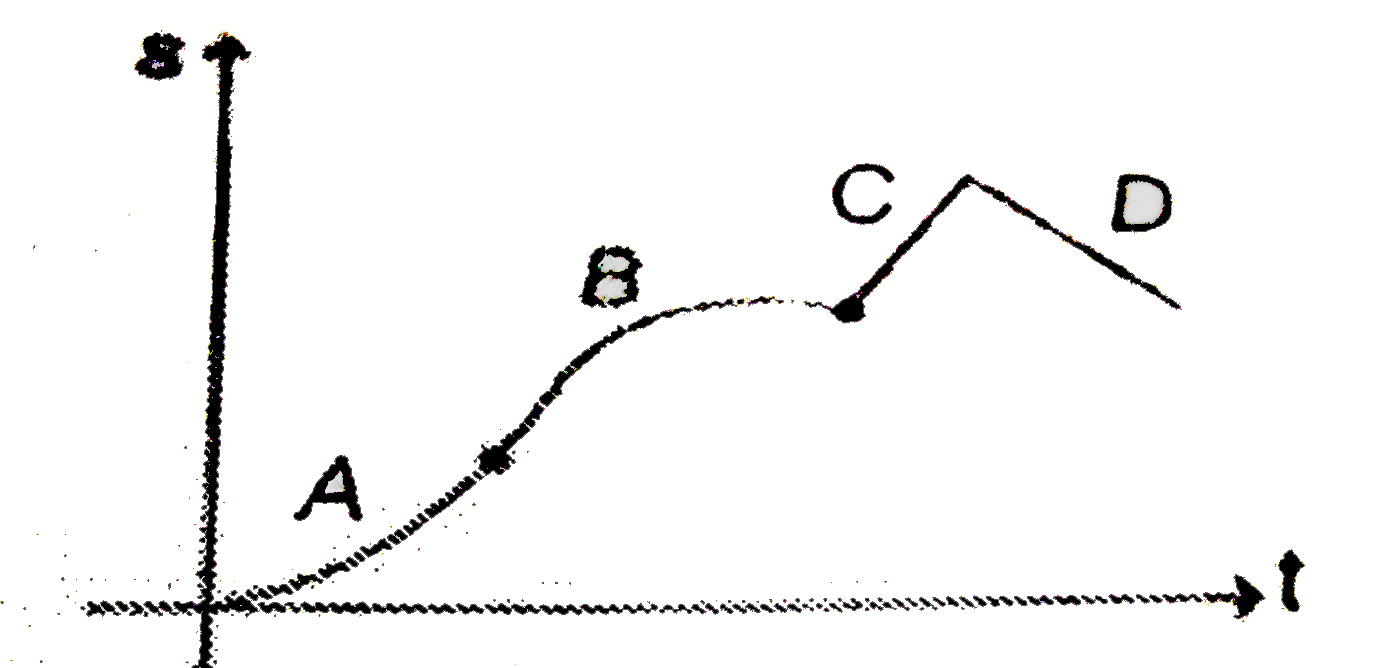
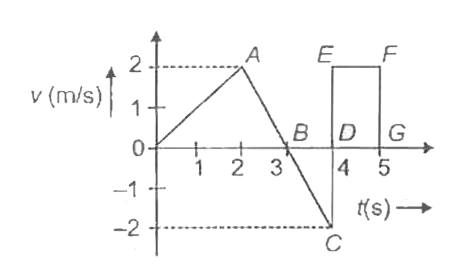
View SolutionThe velocity - time graph of a particle moving along a straight line is shown in the figure given below
The displacement of the particle in 5 second is
View SolutionIf average velocity of particle moving on a straight line is zero in a time interval, then
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. Plot the corresponding displacement-time graph of the particle if at time t=0, displacement s=0.
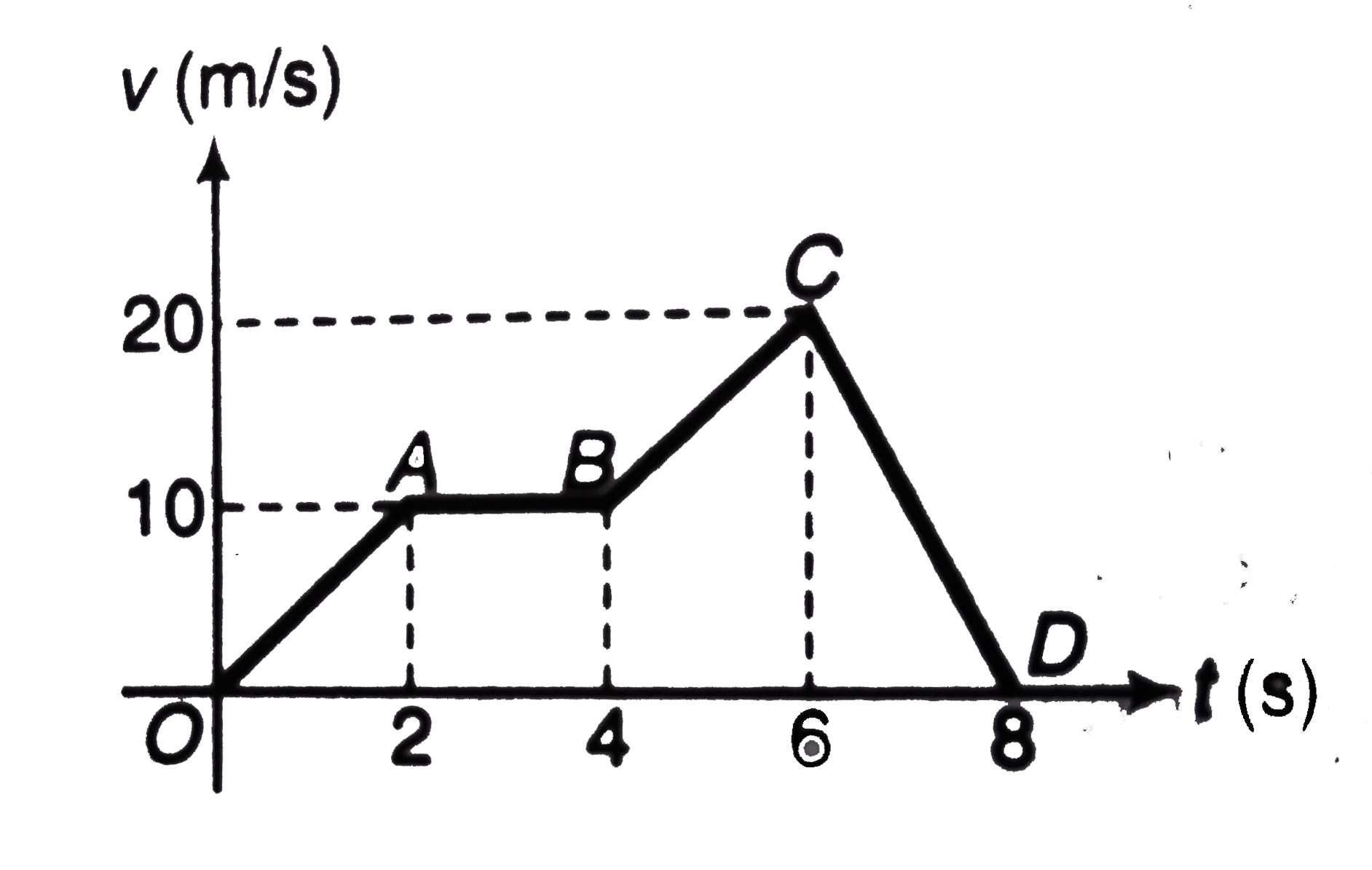
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. Plot the corresponding displacement-time graph of the particle if at time t=0, displacement s=0.

View SolutionThe velocity-time graph of a particle moving in a staight line is shown in the . Find the displacement and the distance trav elled by the particle in 6s.
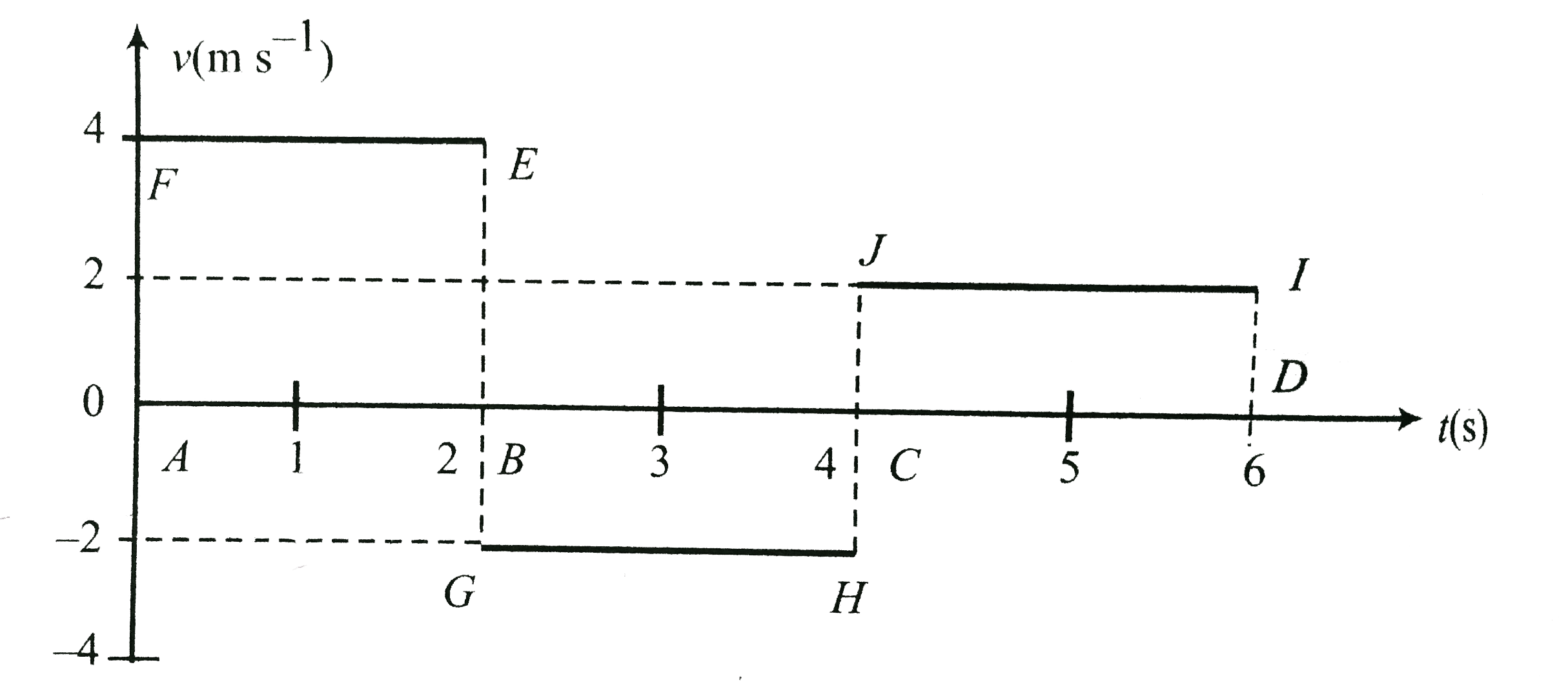 .
.
View SolutionThe velocity (v)-time (t) graph of a partide moving along a straight line is as shown in the figure. The displacement of the particle from t = 0 to t = 4 is
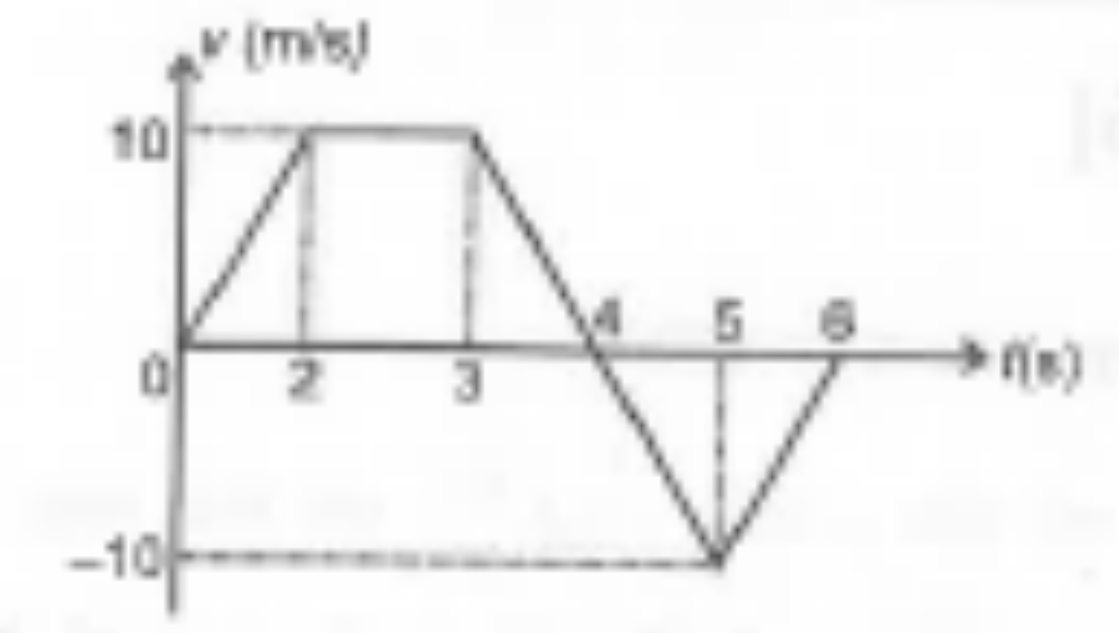
View SolutionThe velocity time graph of a particle moving in a straight line is given line is given in the figure. Then starting from t=0, the particle
View Solution
