Assertion : In spring block system if length of spring and mass of block both are halved, then angular frequency of oscillations will remain unchanged.
Reason : Angular frequency is given by ω=√km .
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:D
(d) k∝1length of spring
If length is halved k will become two times.
from, T=2π√mk
Time period T will remain half for the given conditions.
Similar Questions
Knowledge Check
In the figure all spring are identical having spring constant k and mass m each .The block hav also mass m .The frequency of oscillation of the block is
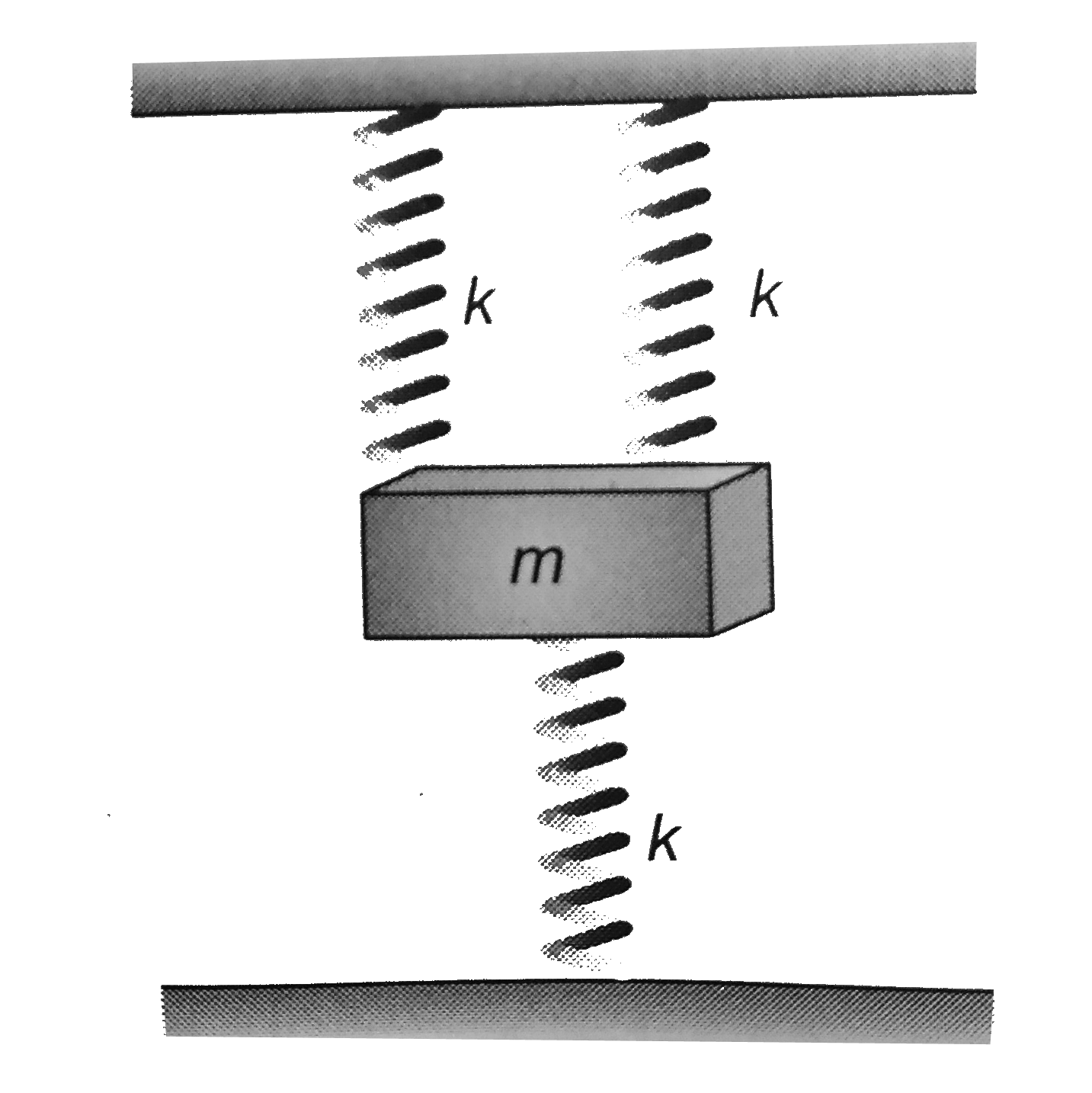 A12π√3kmB12π√3k2mC2π√3m3kDNone of these
A12π√3kmB12π√3k2mC2π√3m3kDNone of theseTwo spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
 A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)
A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)Two equal masses are connected by a spring satisfying Hook's law and are placed on a frictionless table. The spring is elongated a little and allowed to go. Let the angular frequency of oscillations be ω. Noe one of the masses is stopped. The square of the new angular frequency is :
Aω2Bω22Cω23D2ω2
An oscillating block-spring system takes 0.25s to begin repeating its motion. Find (a) the period, (b) the frequency in hertz, and (c ) the angular frequency in radians per second.
View SolutionThe frequency of vertical oscillations of the three spring-mass system, shown in figure, is
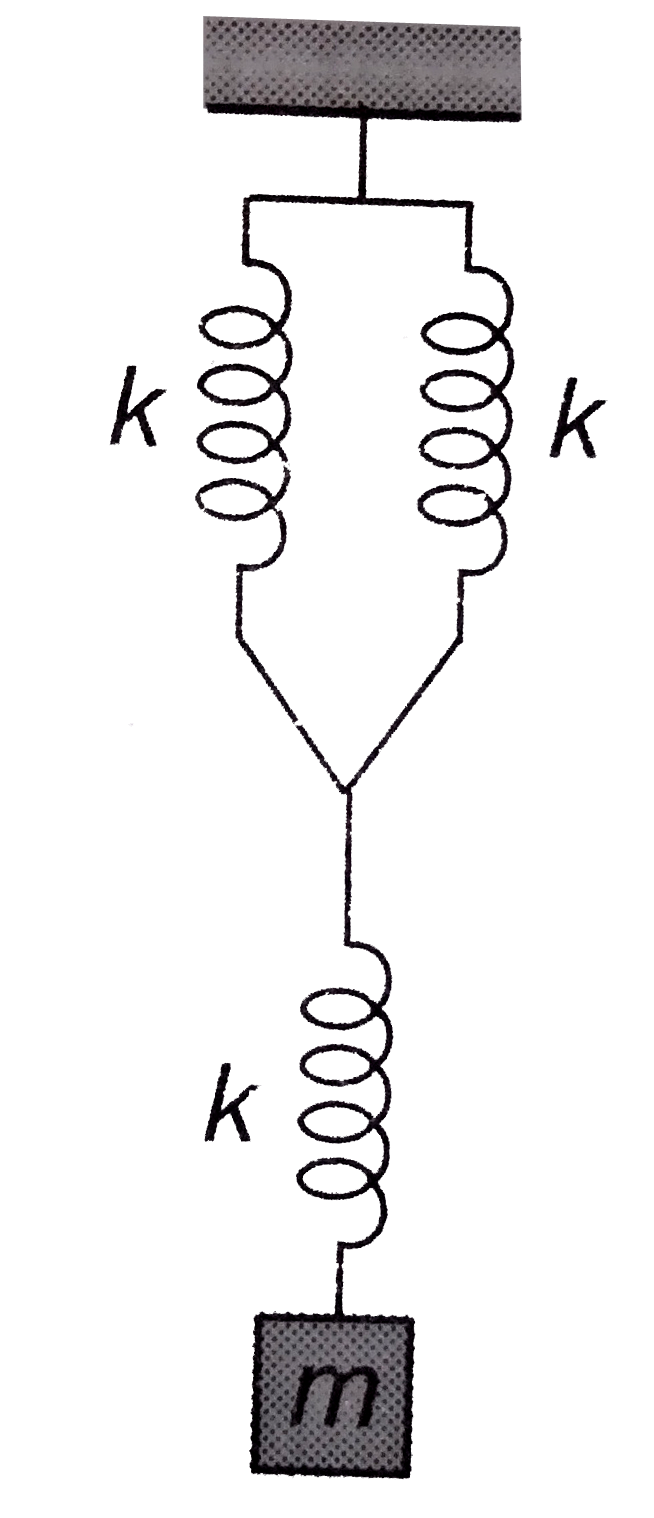
View SolutionPassage VII There is a spring block system in a lift moving upwards with acceleration a=g2
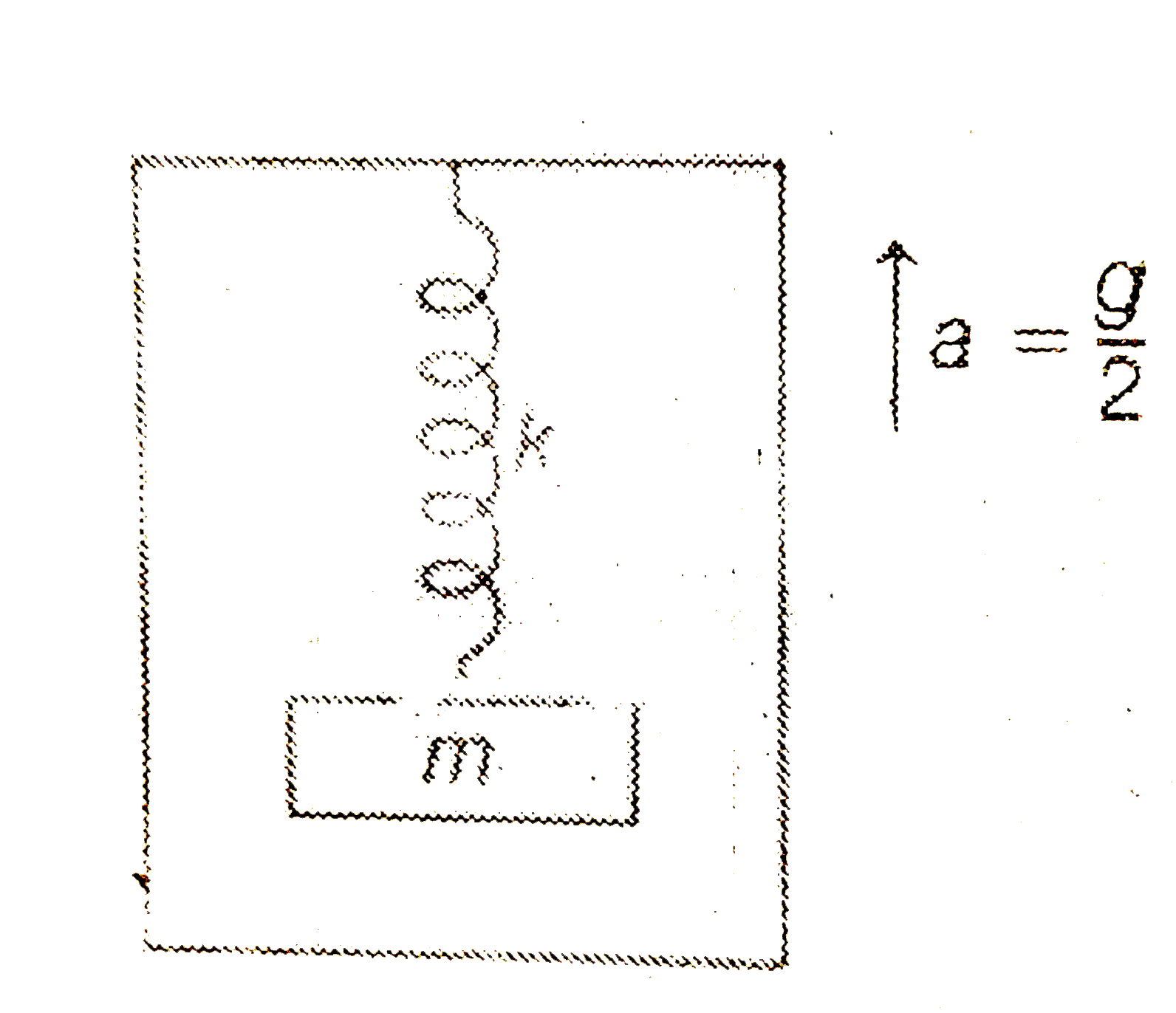
In mean position (of block's oscillations) spring is
View SolutionIf a body of mass 0.98 kg is made to oscillate on a spring of force constant 4.84 N/m the angular frequency of the body is
View SolutionA spring has a force constant k and a mass m is suspended from it the spring is cut in two equal halves and the same mass is suspended from one of the halves. If the frequency of oscillation in the first case is n, then the frequency in the second case will be
View Solution

