Assertion: A block of small m attached to a stiff spring will have large oscillation frequency.
Reason: Stiff springs have high value of spring constant.
If both assertion and reson are true and reason is the correct explanation of assertion
If both assertion and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If both assertion and reason are false.
The correct Answer is:A
Angular frequency, ω=√km as stiff springs have high value of k, so that block will oscillate with large oscillation frequency.
Topper's Solved these Questions
- OSCILLATIONS Book:NCERT FINGERTIPSChapter:OSCILLATIONS Exercise:Exemplar Problems
Explore 1 Video
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTIPSChapter:MOTION IN A STRAIGHT LINEExercise:Assertion And Reason
Explore 15 Videos
- PHYSICAL WORLDBook:NCERT FINGERTIPSChapter:PHYSICAL WORLDExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
There are two springs, one delicate and another stiffer one. Which spring will have a greater frequency of oscillation for a given load ?
View SolutionA mass m attached to a spring A has a frequency of 3 Hz and a spring B has a frequency of 4 Hz.When both spring are connected as shown in the figure, Find the frequency (in Hz)of oscillation.
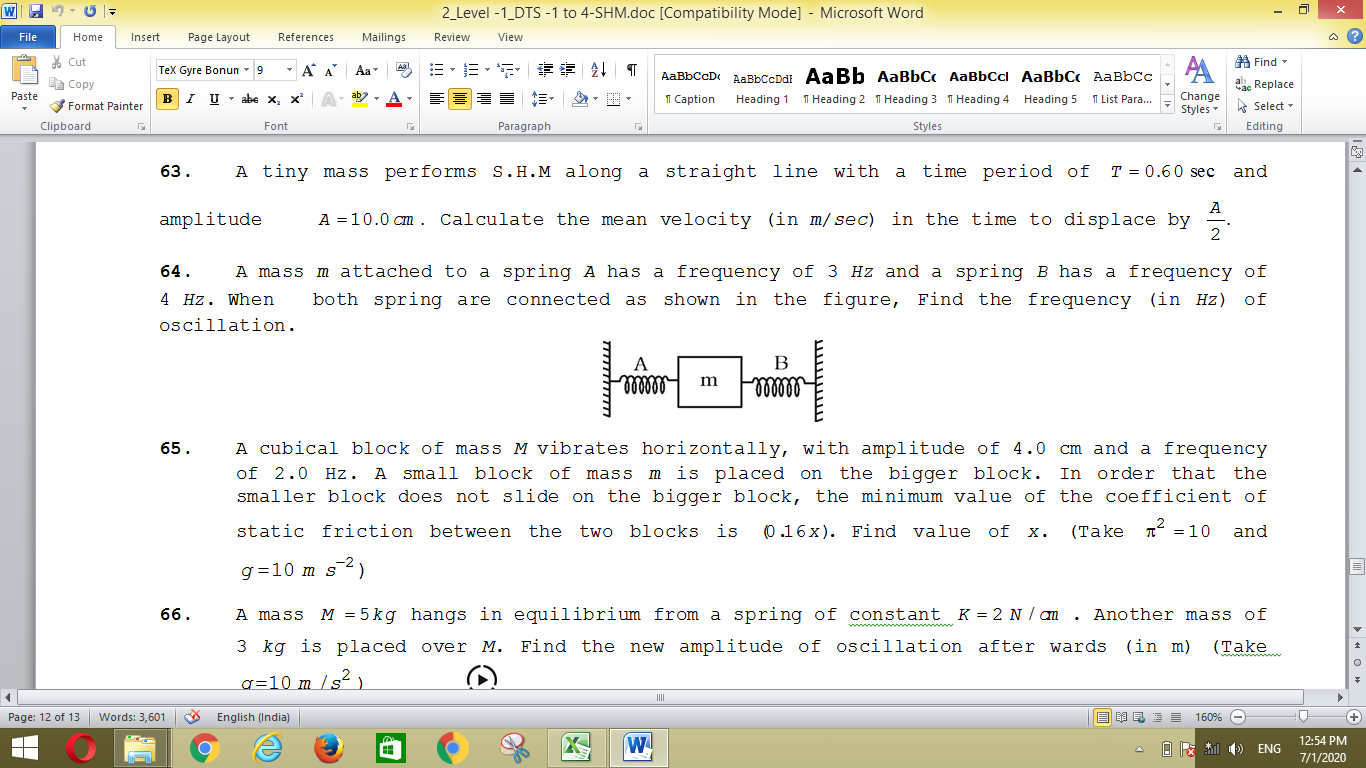
View Solution
Knowledge Check
Block is attached to system of springs. Calculate equivalent spring constant.
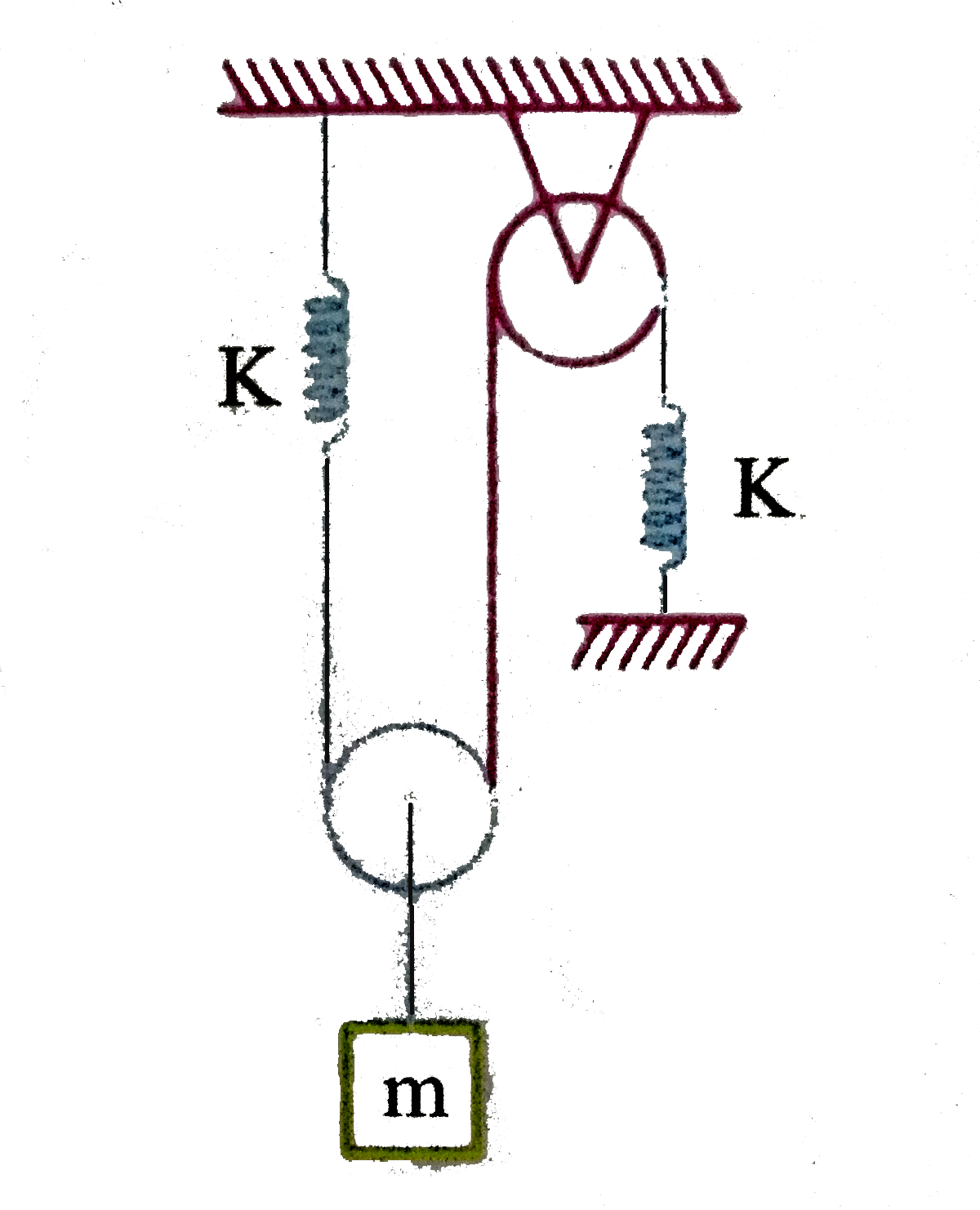 .AKB2KC3KD4K
.AKB2KC3KD4KFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
 A2π√mkBπ√mkC4π√mkD2π√m2k
A2π√mkBπ√mkC4π√mkD2π√m2kIn the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be
 A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk
A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk
Calculate the period of oscillations of block of mass m attached with a set of springs as shown
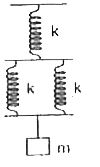
View SolutionA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.

View SolutionA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
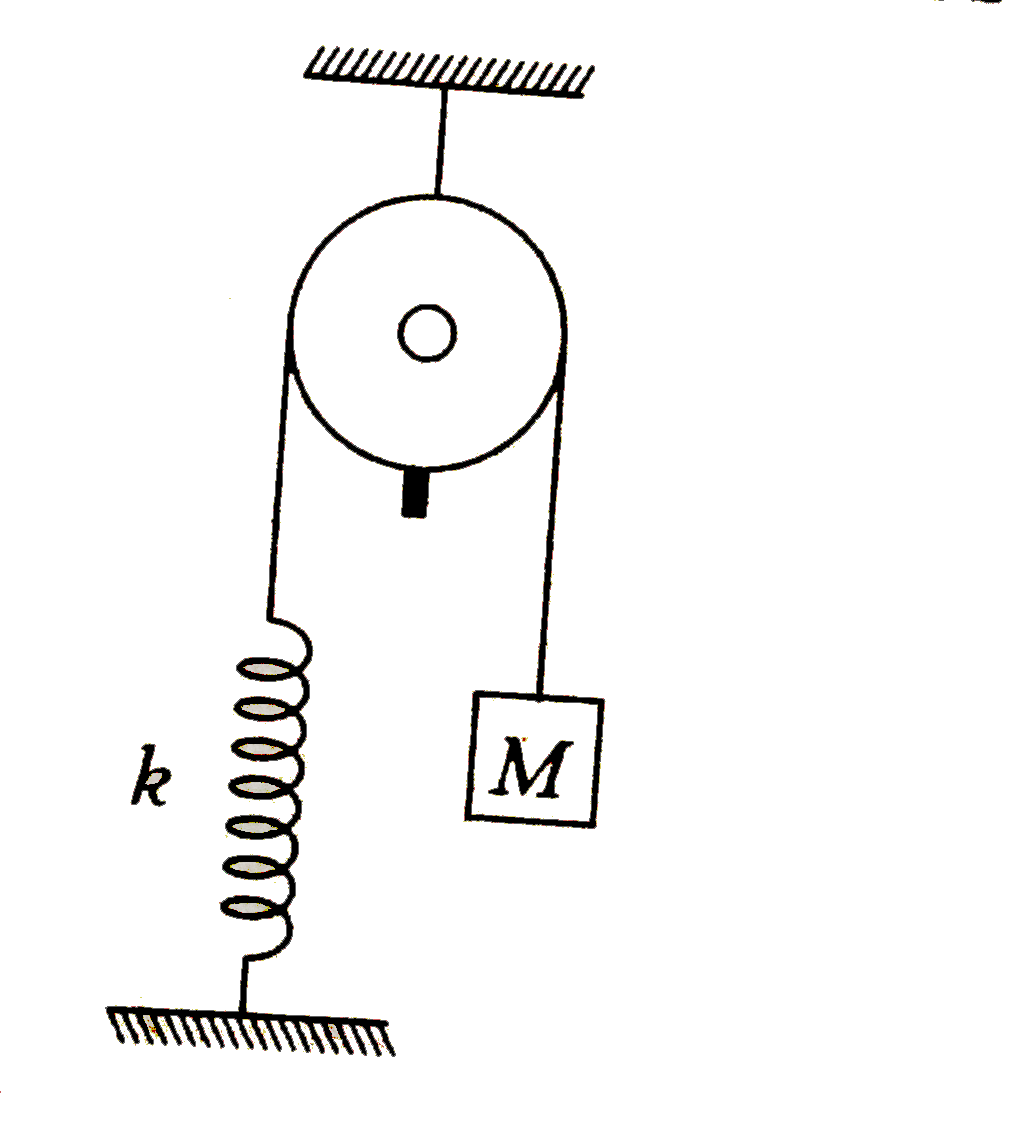
View SolutionA block ofmass m is attached with a spring in its natural length, of spring constant k. The other end A of spring is moved with a constant acceleration 'a' away from the block as shown in the figure−3.74. Find the maximum extension in the spring. Assume that initially block and spring is at rest w.r.t ground frame:

View SolutionTo make the frequency double of a spring oscillator, we have to
View Solution
