Assertion : In x=Acosωt, the dot product of acceleration and velocity is positive for time interval 0<t<π2ω. Reason : Angle between them is 0∘ .
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:A
To solve the problem, we need to analyze the assertion and reason given in the question step by step.
Step 1: Understand the Assertion
The assertion states that in the equation x=Acos(ωt), the dot product of acceleration and velocity is positive for the time interval 0<t<π2ω.
Step 2: Find the Expressions for Velocity and Acceleration
1. Position: Given x=Acos(ωt).
2. Velocity: The velocity v is the derivative of position with respect to time:
v=dxdt=−Aωsin(ωt)
3. Acceleration: The acceleration a is the derivative of velocity with respect to time:
a=dvdt=−Aω2cos(ωt)
Step 3: Analyze the Time Interval
For the time interval 0<t<π2ω:
- At t=0, sin(ωt)=0 and cos(ωt)=1.
- As t increases towards π2ω, sin(ωt) increases from 0 to 1 and cos(ωt) decreases from 1 to 0.
Step 4: Determine the Signs of Velocity and Acceleration
- Velocity: Since v=−Aωsin(ωt), for 0<t<π2ω, v is negative (as sin(ωt) is positive).
- Acceleration: Since a=−Aω2cos(ωt), for 0<t<π2ω, a is negative (as cos(ωt) is positive).
Step 5: Calculate the Dot Product
The dot product of acceleration and velocity is given by:
→a⋅→v=|→a||→v|cos(θ)
Where θ is the angle between →a and →v. Since both →a and →v are negative in this interval, the angle θ between them is 0∘ (they are in the same direction).
Thus, the dot product becomes:
→a⋅→v=|→a||→v|cos(0∘)=|→a||→v|
Since both magnitudes are positive, the dot product is positive.
Step 6: Conclusion on the Assertion
The assertion is true because the dot product of acceleration and velocity is indeed positive for the specified time interval.
Step 7: Analyze the Reason
The reason states that the angle between them is 0∘. This is correct because both acceleration and velocity are in the same direction (both are negative).
Final Conclusion
Both the assertion and reason are true, and the reason correctly explains the assertion.
The assertion states that in the equation x=Acos(ωt), the dot product of acceleration and velocity is positive for the time interval 0<t<π2ω.
1. Position: Given x=Acos(ωt).
2. Velocity: The velocity v is the derivative of position with respect to time:
v=dxdt=−Aωsin(ωt)
3. Acceleration: The acceleration a is the derivative of velocity with respect to time:
a=dvdt=−Aω2cos(ωt)
For the time interval 0<t<π2ω:
- At t=0, sin(ωt)=0 and cos(ωt)=1.
- As t increases towards π2ω, sin(ωt) increases from 0 to 1 and cos(ωt) decreases from 1 to 0.
- Velocity: Since v=−Aωsin(ωt), for 0<t<π2ω, v is negative (as sin(ωt) is positive).
- Acceleration: Since a=−Aω2cos(ωt), for 0<t<π2ω, a is negative (as cos(ωt) is positive).
The dot product of acceleration and velocity is given by:
→a⋅→v=|→a||→v|cos(θ)
Where θ is the angle between →a and →v. Since both →a and →v are negative in this interval, the angle θ between them is 0∘ (they are in the same direction).
→a⋅→v=|→a||→v|cos(0∘)=|→a||→v|
Since both magnitudes are positive, the dot product is positive.
The assertion is true because the dot product of acceleration and velocity is indeed positive for the specified time interval.
The reason states that the angle between them is 0∘. This is correct because both acceleration and velocity are in the same direction (both are negative).
Both the assertion and reason are true, and the reason correctly explains the assertion.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Miscellaneous Examples
8 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Knowledge Check
If 0<x<π2 and tanx=a2, then cos x =
A2√a2−4Ba√a2−4C2a+2D2√a2+4
Assertion : In x=Acosωt, x is the displacement measured from extreme position.
Reason : In the above equation x=A at time t=0.
View SolutionAssertion : In x=Acosωt, x is the displacement measured from extreme position.
Reason : In the above equation x=A at time t=0.
View SolutionA particle is executing SHM according to the equation x=Acosωt. Average speed of the particle during the interval 0≤t≤π6ω is
View SolutionThe number of solution of |cos x| =sin x in the interval 0<x<4π is _________
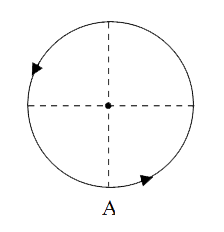
View SolutionA particle is describing uniform circular motion in the anti-clockwise sense such that its time period of revolution is T. At t = 0 the particle is observed to be at A. If θ1 be the angle
between acceleration vector at t=T4 and average velocity vector in the time interval 0 to T/4 and θ2 be the angle between acceleration vector at t=T4 and the vector representing change in velocity in the time interval 0 to T/4, then :
View SolutionAssertion : In the υ−t diagram as shown in figure, average velocity between the interval t = 0 and t=t0 is independent of t0
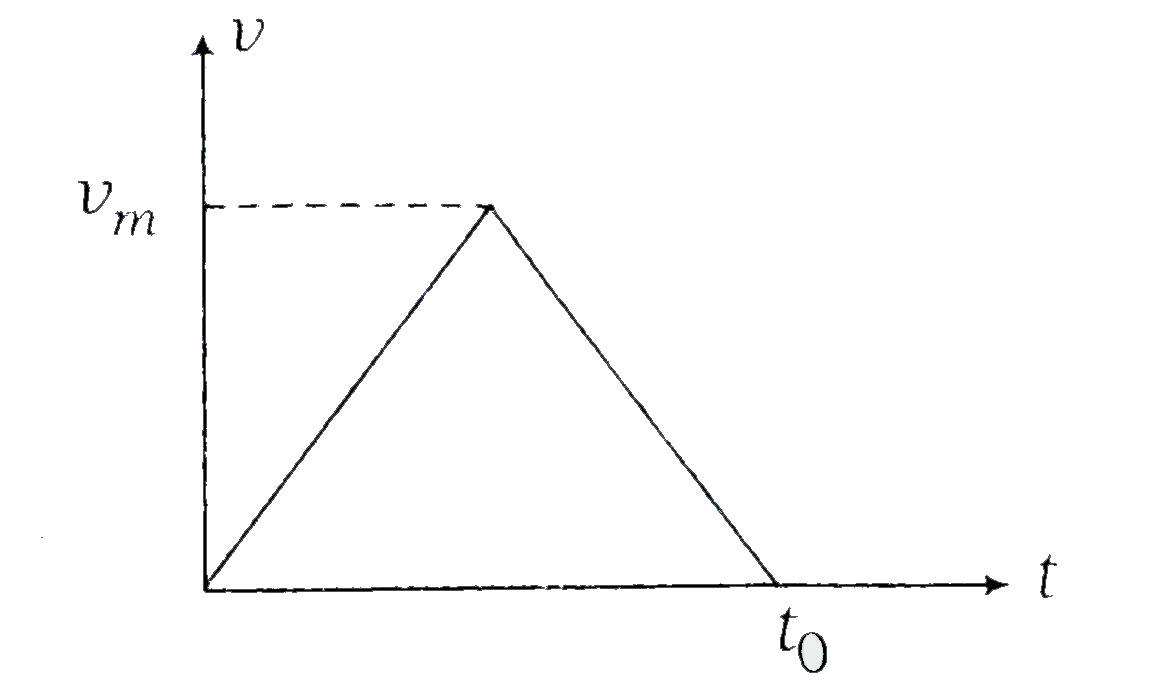
Reason : Average velocity in the given interval is 12υm.
View SolutionA particle moves along the x - axis according to x=A[1+sinωt]. What distance does is travel in time interval from t=0 to t=2.5π/ω ?
View Solution
