Assertion : Two identical spherical balls are released from two inclined plane. First is sufficiently rough and second is smooth. Both the balls will have same kinetic energy on reaching the bottom
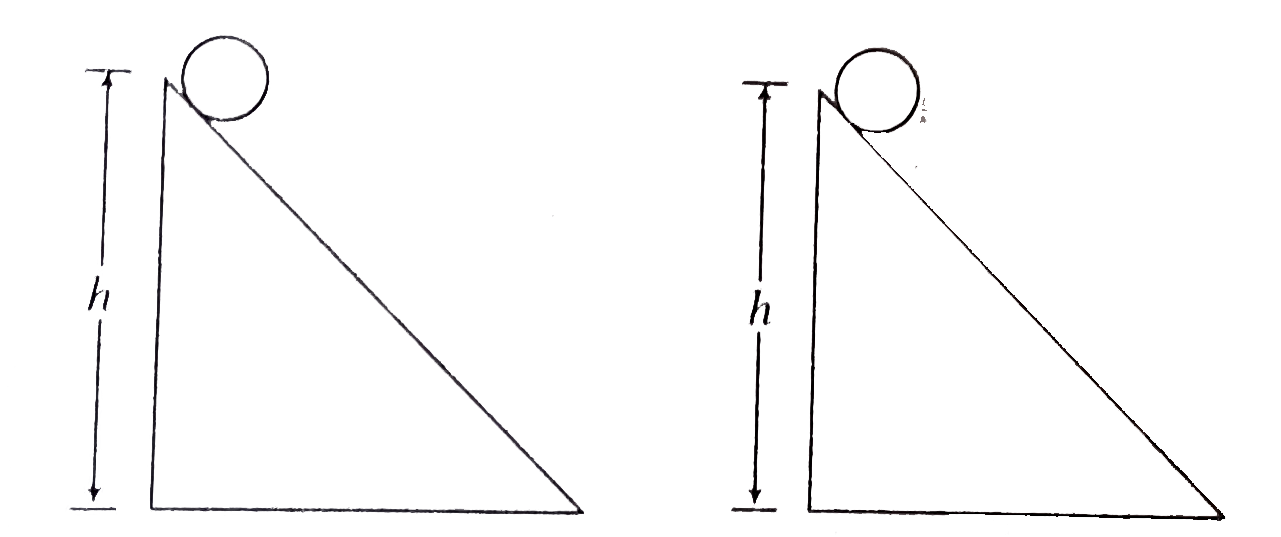
Reason : Linear velocity of second ball will be more.
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion
If Assertion is true but Reason is fasle
If Assertion is false but Reason is true
The correct Answer is:B
In first case, work done by friction will be zero. That's why mechanical energy will remain conserved. Further, in second case, linear velocity will be more because this ball has only translation kinetic energy.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (A) Chapter Exercises
83 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions

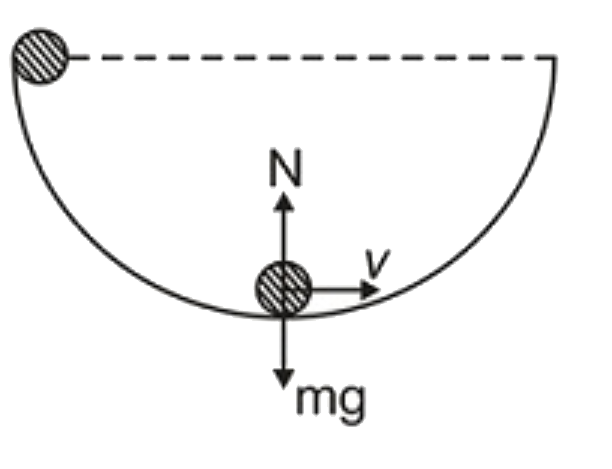
A small ball is released from rest from point A as shown. if bowl is smooth, than ball will exert more pressure at point B, compared to the situation if bowl is rough.
Reason: Linear velocity and hence, centripetal force in smooth situation is more.
View SolutionIn both the figures, all other factors are same, except that in figure (i) AB is sufficiently rough and BC is smooth while in figure (ii) AB is smooth and BC is sufficiently rough. Kinetic energy of the ball on reaching the bottom:

View SolutionA uniform solid spherical ball is rolling down a smooth inclined plane from a height h. The velocity attained by the ball when it reaches the bottom of the inclined plane is v. If ball when it reaches the bottom of the inclined plane is v. If the ball is now thrown vertically upwards with the same velocity v, the maximum height to which the ball will rise is
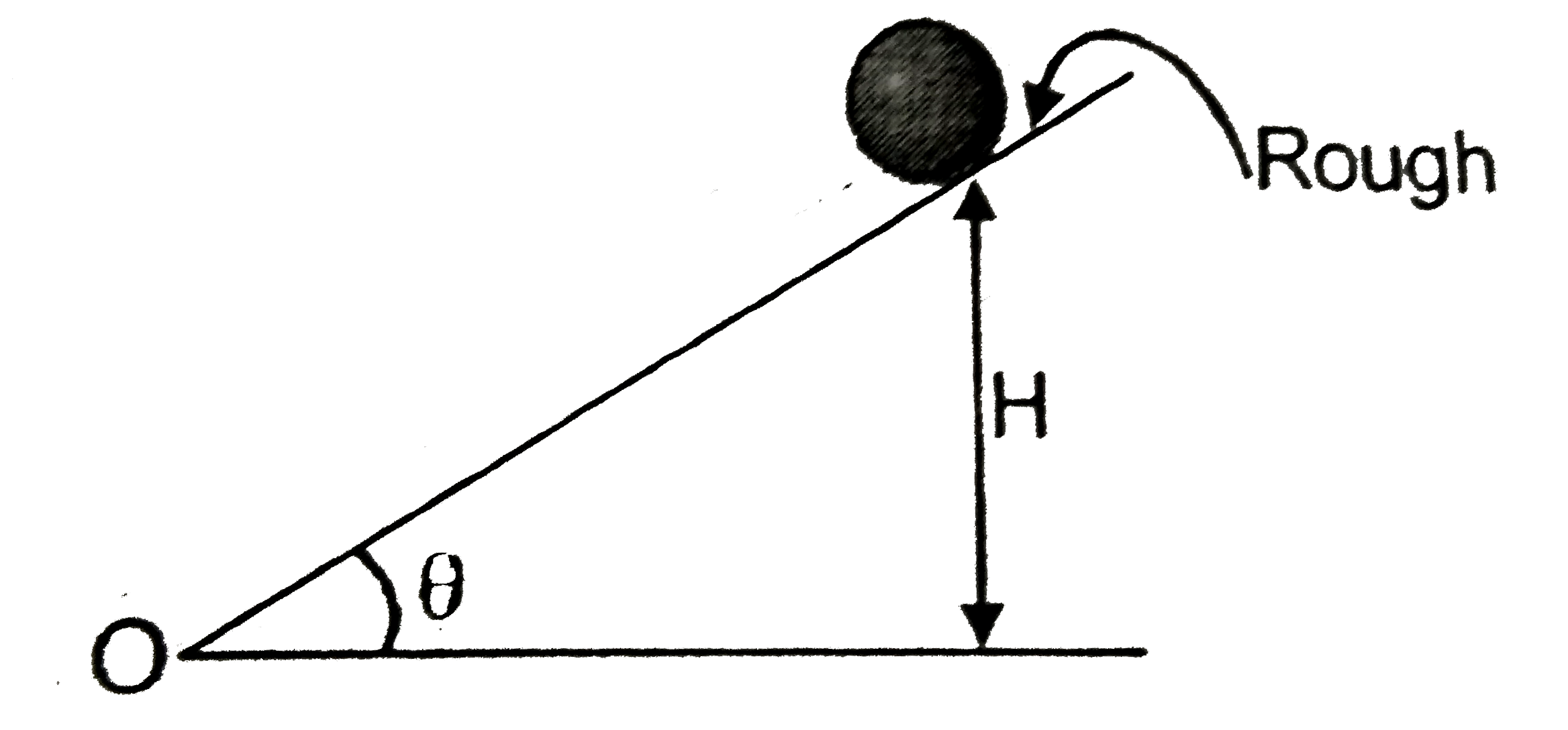
View SolutionA solid ball of mass 'm' is released on a rough fixed inclined plane from height H. The ball will perform pure rolling on the inclined plane. Then
View SolutionA ball is released from point A. During its motion ball takes two seconds from B to C Find the time taken by ball from A to C.
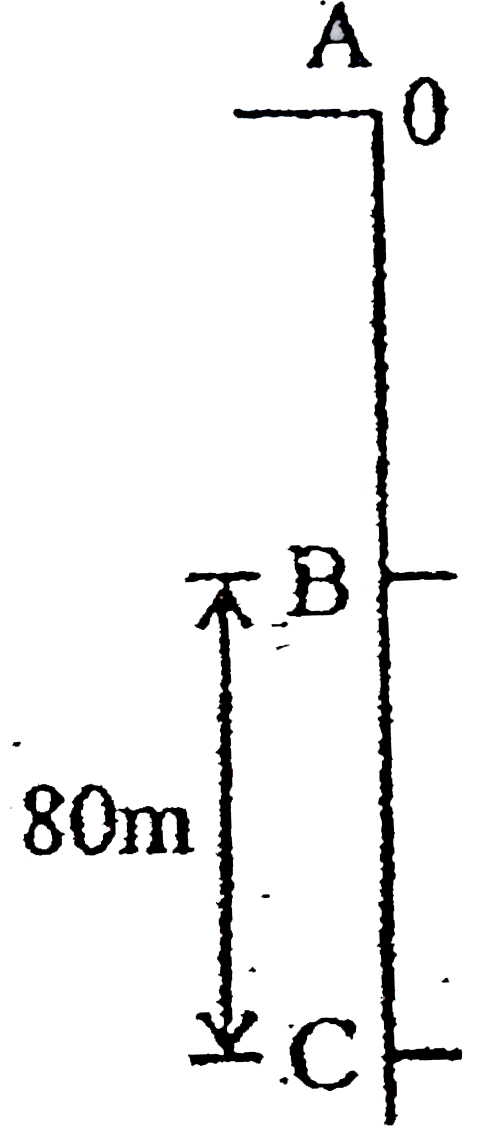 .
.
View SolutionA solid spherical ball of mass m is released from the topmost point of the shown semi - spherical shell. The track is sufficiently rough to enablle to enable pure rolling motion. The normal force between the ball and the shell at the lowest position is
View SolutionA solid spherical ball is rolling without slipping down an inclined plane. The fraction of its total kinetic energy associated with rotation is
View SolutionAssertion : A solid sphere and a ring of same mass and radius are released simultaneously from the top of an inclined surface. The two objects roll down the plane without slipping. They reach the bottom of the incline with equal linear speeds
Reason : Decrease in potential enery for both is the same.
View SolutionA solid spherical ball is released from rest on an incline of inclination angle θ (which can be varied ) but through a fixed vertical height h. The coefficient of static and kinetic friction are both equal to μ. If E represents the total kinetic energy of the ball at the bottom of the incline as a function of the angle of inclination θ. W represents the work done by friction for the whole time of motion as a function of the angle of inclination θ. Choose of correct graph (s)
View Solution
A curved suface is shown in figure. The portion BCD is free of friction. There are three spherical balls of identical radii and masses. Balls are released from rest one by one from A which is at a slightly greater height than C.
Wioth the surface AB, ball 1 has large enough friction to cause rolling down without slipping, ball 2 has a small friction and ball 3 has a negligible friction.
(a) For which ball is total mechanical energy conserved?
(b) Which ball(s) can reach D?
(c )For ball which do not reach D, which of the balls can reach back A?
View Solution
